完整翻译：05 1988：记忆的两个组成成分
记忆的两个组成成分
多年来，研究者使用记忆强度来反映对信息记忆得有多好，然而一个变量并不足以描述长期记忆的状态。
遗忘是一个概率问题，我们需要用一个变量来衡量记忆后不同时间能够回忆起的概率。
有了回忆概率，我们自然还想知道，这个概率关于时间的变化率，这就需要第二个变量来衡量回忆概率衰减的速度。
这里依然有直觉的成分，例如：
- 时间越长回忆起来的概率越低；
- 复习后遗忘的速度是先快后慢；
- 多次复习后遗忘的速度下降了。
假设
假设回忆概率 R 是以 e 为底的负指数函数，随着时间 t 增加而下降，并将回忆概率衰减常数的倒数称为记忆稳定性 S。
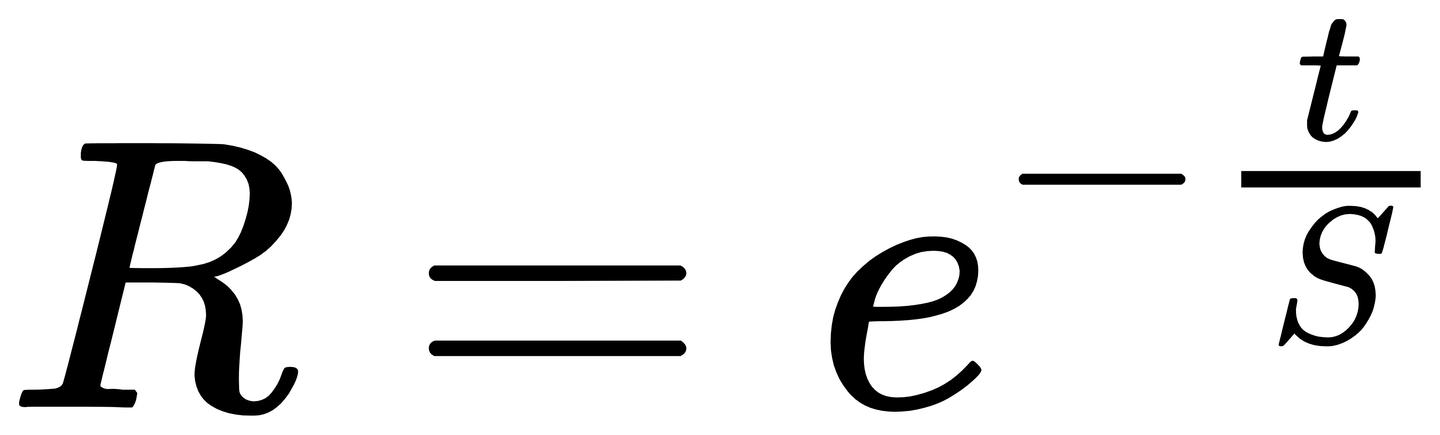
这个假设符合上文提及三个直觉。t 越大，R 越小，R 的变化率也越小。且 S 越大，R 下降的速度也变慢了：
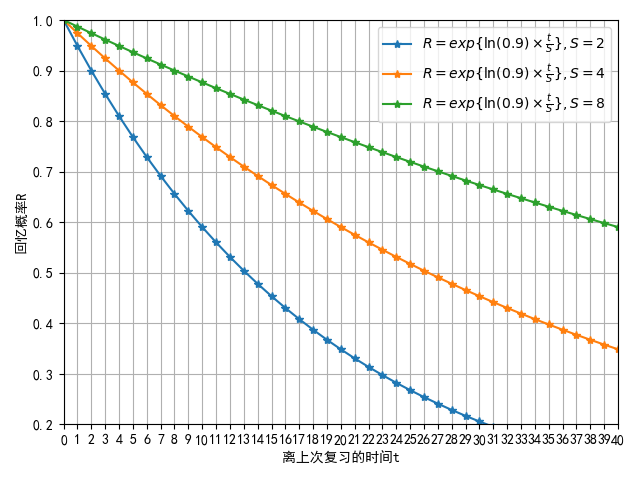
多次复习后遗忘的速度下降则可以表示为：每次回忆成功的复习都会增加记忆稳定性 S。而平时不复习的时候，回忆概率 R 随时间下降，记忆稳定性 S 保持不变。
当然，这里依然有两个现象需要注意：
- 短时间内的频繁重复几乎不能增加记忆稳定性，也就是所谓的间隔效应；
- 遗忘时，记忆稳定性迅速下降（不确定）。
同时，在现实生活中，学习材料的难度并不是单一的。直觉上，难度也会影响到记忆，即越难的内容越不好记忆。所以 SuperMemo 引入了第三个变量。
记忆的三个变量
Memory stability(S): 记忆稳定性，即回忆概率为 90% 时的平均间隔（天数）
Memory retrievability(R): 记忆可提取性，即任意时刻的回忆概率
Item difficulty(D): 卡片难度
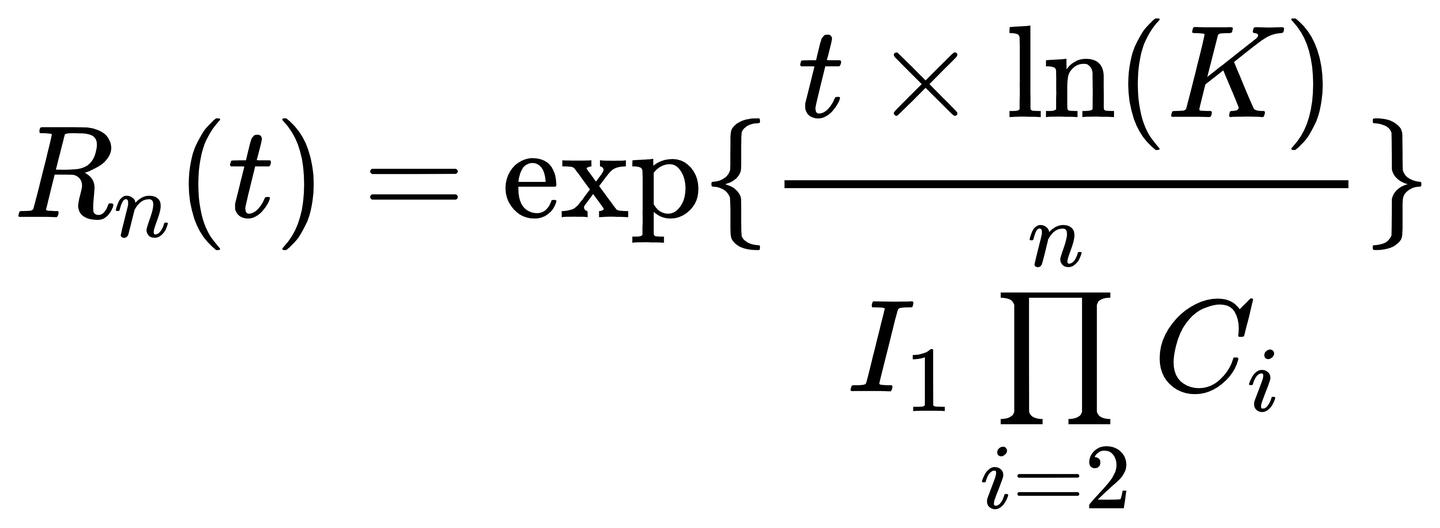
，即按照最优复习间隔复习 n 次后 t 时刻的回忆概率
，即保留率，默认为 90%
，即第一个间隔长度（天数）
important!:
，即第 i-1 次复习的最优复习间隔的比例。在后来的实验中发现，其并不是一个常数，而是受以下参数影响：
- 记忆稳定性 S：记忆越持久，
越小（即随着稳定性增长，其增长潜力在逐渐下降。这意味着持久的记忆并不能简单地变得更加持久）
- 例如：难度为 3 的
到
分别为 3, 1.9, 1.6, 1.5, 1.4
- 当然，C 总是大于 1 的（在 SuperMemo 中恒大于 1.2），即稳定性在复习成功时总是增长的。
- 记忆可提取性 R：回忆概率越低，
- 例如：预计 7 天后复习，实际 12 天后复习，可提取性更低，若回忆成功， C 应更大
- 卡片难度 D：卡片越难，
- 例如，难度为 6 到 3 （数值越小越难）的卡片的
由于这种多重关系， 的精确值不容易预测，后来 SuperMemo 用多维矩阵来表示
的多自变量函数，并在实际学习过程中调整矩阵的值，从而解决了这个近似优化问题。
在 SM-17 中， 被命名为 SInc(Stability increase)，即稳定性增长。因为在公式中
正好表示了每一次重复的记忆稳定性，而
正好是重复前后记忆稳定性的增长倍数。
研究了很久，整理了 2 万多字的文档，为了写一个浓缩通俗版，我尽力了。有任何疑惑，欢迎在评论区讨论。