还挺多的,省流:
- 用知识图谱构建学科结构
- 用学生模型(结合间隔重复)精准画像
- 用诊断算法快速定位知识边界
- 用任务选择算法(融合精熟学习、交错学习、间隔重复等策略)规划最优学习路径
以下内容摘自 @Thoughts Memo 汉化组的译文《Math Academy 的 AI 是如何工作?》
Math Academy 的人工智能(AI)是一个专家系统,它能模拟优秀辅导教师的决策过程,针对学生在任何特定时间点应该处理哪些学习任务给出建议。这一功能的实现,得益于以下几项关键技术的结合。
知识图谱储存了优秀辅导教师所应掌握的关于数学学科体系的全部信息。具体包含哪些知识主题?每个主题内最简单和最困难的题型变式分别是什么?学生若要学习各个主题,必须具备哪些背景知识?如果学生在解答某一特定类型的问题时遇到困难,哪些具体的背景知识点与他们当前面临的困境最为相关?所有这些问题(以及更多其他问题)的答案,都储存在我们的知识图谱之中。
学生模型会接收学生的作答,将其与知识图谱进行比对分析,从而判断学生掌握了哪些知识主题,以及掌握的程度如何。这便是所谓的学生知识画像。为了构建学生的知识画像,我们的学生模型采用了间隔重复,这是一种系统性的方法,用以判断先前学习过的内容何时需要复习。
诊断算法充分利用知识图谱,力求以最少的题目数量来评估学生的知识画像。该算法能够识别出学生已经掌握的课程内容,以及其基础知识中存在的薄弱环节。
任务选择算法会根据学生的知识画像,来确定能够最有效地促进学生学习进展的最优学习任务。学生下一步应该学习什么新内容?他们又需要复习哪些旧知识?在回答这些问题时,我们的任务选择算法始终致力于最大化学生在系统上单位学习时间内所能获得的学习量。
知识图谱
在数学的图论这一领域中,「图」这个词指的是一种由若干对象以及连接这些对象的箭头所构成的示意图。在我们的知识图谱中,这些对象便是各个数学知识主题,而它们之间的箭头则代表着各种关系,例如某个主题是学习另一个主题的前置知识。(实际上存在许多不同类型的关系,其中一些甚至涉及到主题内部更为细致的「亚原子级别」的构成要素——但目前,我们仅重点关注主题之间的前置知识关系。)
举例来说,下方这个小型的知识图谱展示了主题 异分母分数加法(顶层)拥有两个前置知识:1) 运用模型进行异分母分数加法,以及 2) 分数与整数加法(中层);而这两个前置知识各自又拥有一个共同的前置知识,即 运用模型进行分数与整数加法(底层)。
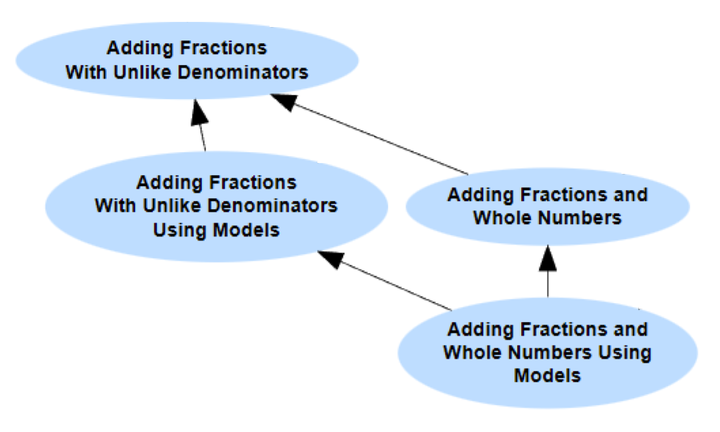
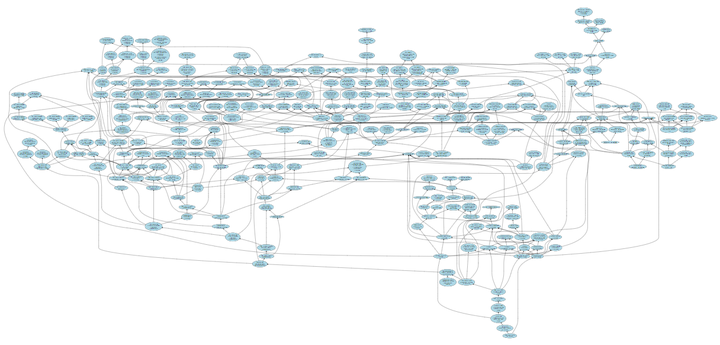
知识图谱能够将大量复杂的信息进行编码,若非如此,这些信息将难以描述和进行逻辑推理。从一个更宏观的视角来看,下方展示的是一门包含约 300 个知识主题的完整课程所对应的知识图谱。
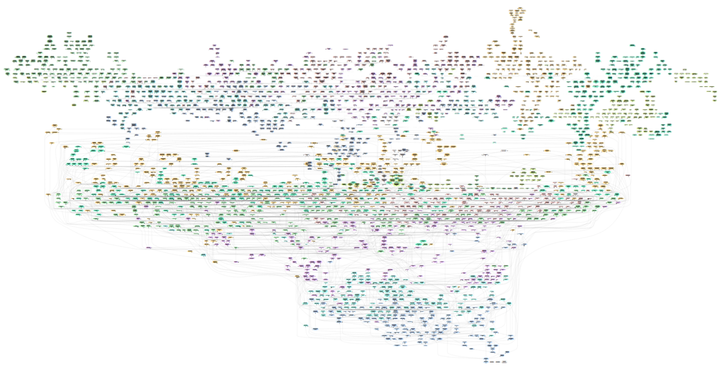
在最宏观的视角下,Math Academy 的整体课程体系由数千个相互关联的知识主题构成,内容横跨从小学四年级至大学阶段的数学知识。所有这些主题都在知识图谱中紧密相连。从这个角度看,一门课程实质上就是我们知识图谱中的一个特定区域。(在下方的可视化示意图中,不同的颜色代表不同的课程。)
学生模型
我们的学生模型依据学生的作答记录来构建其知识画像。通俗地讲,一名学生的知识画像反映了其数学思维能力的发展程度。每当学生学习一个新的数学知识点,就好比他们长出了一个新的脑细胞,并将其与已有的脑细胞连接起来。起初,这个新的脑细胞还比较「脆弱」,需要频繁地「滋养」;但久而久之,它会变得「强壮」,所需的「照料」频率也会随之降低。
例如,下方可视化呈现了一名学习第二学期微积分课程的学生的知识画像。图中已学习的知识主题用深浅不一的颜色标出(颜色越深代表已完成的有效练习越多),而主题之间的箭头则表示它们之间的前置知识关系。(请注意:下方展示的知识画像仅仅是该学生完整「数学大脑」中的一个「子系统」——虽然下方的微积分课程包含数百个知识主题,但我们从小学到大学阶段的完整数学课程体系则涵盖了数千个主题。)
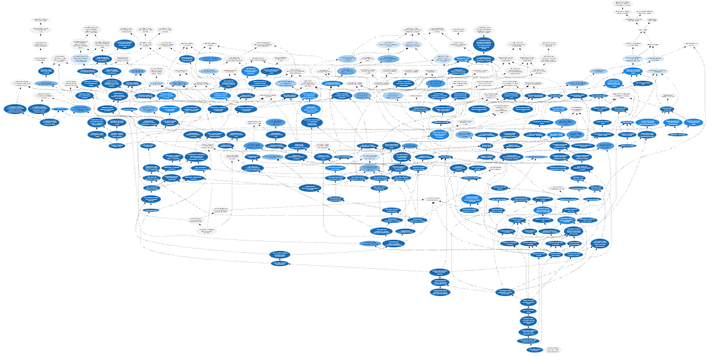
更准确地来说,一名学生的知识画像衡量了他们在每个知识主题上累积了多少次「间隔重复」练习。「间隔重复」,亦称「分散练习」,是一种系统性的复习方法,用于回顾先前学习过的材料,它巧妙地利用了「间隔效应」:当复习活动分散在多个时间段进行(而非集中在一次学习中死记硬背)时,记忆不仅能够得到恢复,更能进一步巩固成长时程记忆,从而减缓遗忘速度。因此,完成的复习次数越多(并且这些复习在时间上得到合理安排),记忆保持的时间就越长,距离下一次需要复习的时间间隔也就可以相应拉长。基于此,「一次间隔重复」可以被理解为在恰当的时机进行一次富有成效的复习,且复习量达到了最小有效剂量。
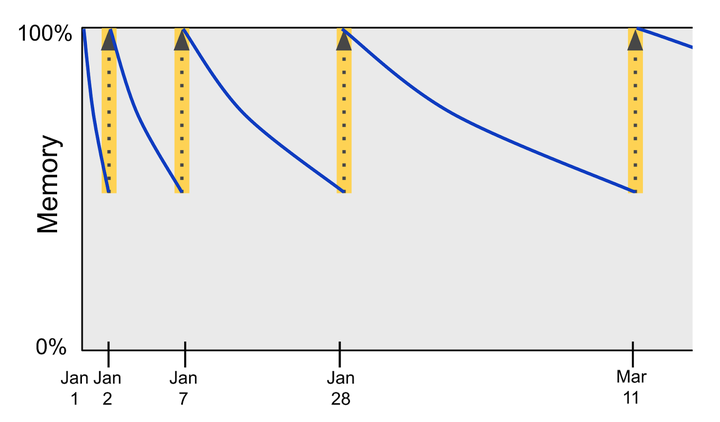
间隔重复算法
间隔重复算法旨在判断学生是否到了应该复习先前所学知识主题的时刻。
- 如果某项复习内容逾期过久,学生便会遗忘过多,导致其在间隔重复的进程中出现倒退。
- 然而,倘若复习进行得太早,学生记忆强化的效果会打折扣,学习进度也会因此减缓。(这种情况并不理想,因为它效率低下:时间本应用于学习新知识主题,或复习那些确实已到复习期限的主题。)
现有的间隔重复算法大多局限于独立抽认卡的应用场景——但这并不适用于像数学这样具有严密层级结构的知识体系。例如,当一名学生练习两位数加法时,他们实际上也在同时练习一位数加法!总体而言,针对高阶知识主题的重复练习,其效果应当沿着知识图谱「涓滴」下去,从而更新那些因学习高阶知识而得到隐式练习的基础主题的复习计划。
让重复练习的效果沿着知识图谱涓滴,表面听来或许简单明了,但其细节之处却暗藏诸多复杂因素:
- 前置知识主题并非总能得到隐式练习——有时,学生需要先熟悉某个前置知识才能理解新的主题,但该前置知识点本身并未在学习新主题的过程中得到充分练习。因此,重复练习的效果不能简单地涓滴至前置知识主题。相反,它们必须涓滴至那些「被包含」的主题,即那些作为构成性技能而被隐式练习的更基础的主题。
- 隐式重复练习的效果需要进行适当折算:这类练习发生的时间往往过早,不能完全等同于一次针对「被包含」主题的有效复习,并以此来计算下一次复习的时间。
- 包含关系通常是部分的:构成性技能往往只得到部分练习,而非完整练习。
此外,当学习任务包含多个问题时,计入间隔重复的权重也需要根据学生的具体表现而有所不同。为了全面地考虑到所有这些细节因素,我们开创了一套全新的间隔重复理论,称之为「部分隐式间隔重复(Fractional Implicit Repetition, FIRe)」。
诊断算法
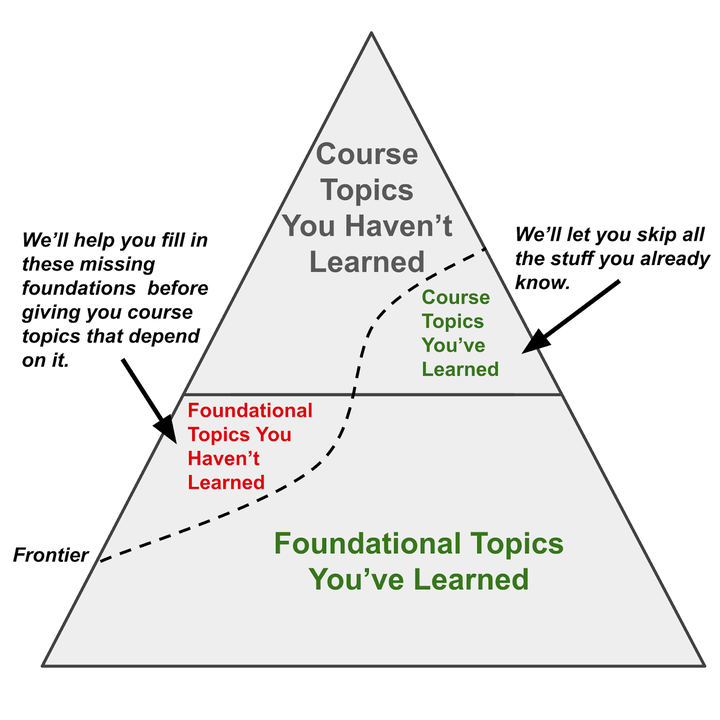
当学生加入 Math Academy 时,他们会参加一项自适应诊断测试。该测试借助知识图谱来快速评估学生的知识画像。具体而言,它致力于识别学生的「知识边界」——即学生已知知识与未知知识之间的分界线。知识边界标示了学生当前已准备好学习的知识主题。
我们的诊断服务专为特定课程量身打造——但在评估课程内容掌握情况的同时,也会评估学生为顺利完成该课程所必须具备的早期阶段基础知识。新加入的学生往往缺乏某些基础知识。这种情况在传统课堂中或许会导致学习困难,但我们的诊断系统即便在学生的知识边界低于其当前课程水平时,也能够准确评估出来。诊断结束后,我们会帮助学生弥补所有缺失的基础知识,同时允许他们学习那些不依赖于这些缺失基础的课程主题。
若没有精巧的算法支持,要推断出学生的知识边界,势必需要进行海量的诊断测试。一门课程通常包含数百个学生可能已经掌握的知识主题,再加上两倍于此、学生可能缺失的基础主题,总计约有 500 至 1000 个知识主题需要评估。然而,借助一种新颖的诊断题目选择算法,我们能够将诊断题目的数量减少一个数量级。
该算法首先会将知识图谱压缩,筛选出能够以足够精细的粒度级别完全「覆盖」一门课程及其所有基础知识的最少核心主题。然后,它会反复选择那些评估结果能为构建学生知识画像提供最多信息的知识主题。学生的每一个正确答案,都为他们掌握该主题、其前置知识及其他相关主题提供了正面证据;反之,每一个错误答案则为他们尚未掌握该主题、其「后置条件」及其他相关主题提供了负面证据。
当面对相互矛盾的证据时,诊断算法会仔细权衡正面证据与负面证据,从而对学生的知识状况形成一个高度细致入微的诊断,并且能像真人辅导老师一样,根据后续的观察结果进行灵活调整。
- 例如,如果一名学生提交了正确答案,但所用时间远超已掌握该主题的学生通常所需的预期时间,那么这份证据的权重就会被调低(因为这名学生很有可能尚未充分掌握该主题,不足以在此基础上继续学习新知识)。
- 同样地,如果综合所有证据后,学生仅以微弱差距未能完全掌握某些主题,系统会将这些主题视为「有条件完成」。起初,系统会假定学生已掌握这些主题并分配相应任务,但如果学生在学习过程中遇到困难,系统便会立即沿着相应的学习路径开始「向后回溯」进行巩固。
任务选择算法如何为学生挑选新的学习主题
在决定学生接下来应该学习或复习哪些知识主题时,我们始终致力于最大化学生在单位学习时间内所能获得的学习成效。为达成此目标,我们运用了多种认知学习策略,包括精熟学习、递进学习、间隔重复、交错学习以及最小化联想干扰策略。
在精熟学习中,学生需要先证明自己已熟练掌握了前置知识,然后才能进入更高级知识主题的学习。
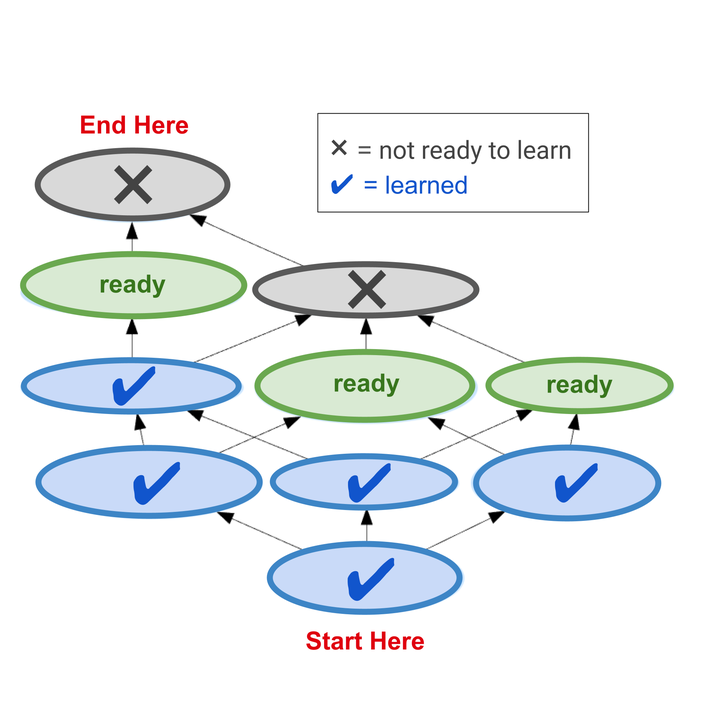
我们通过「递进学习」将精熟学习法推向了更高层次,也就是说,一旦学生证明其已掌握了前置知识,便会立即引导他们学习新的知识主题。当学生通过这种方式不断在原有知识的基础上递进新层次的知识,并在此过程中运用到前置知识或构成性知识时,他们原有的知识便会变得更加巩固、条理清晰且理解透彻。这增强了他们知识体系的结构稳固性,也使得吸收新知识变得更为容易。当然,学生确实会定期复习先前学习过的内容,但他们不会被不必要地「拖慢」进度去过度练习已学过的主题。学生完成一节课程后,新的课程便会即时解锁。
我们的任务选择算法还会致力于最小化「联想干扰」。这是一种学习阻力,当关联性极强的若干知识点被同时或在极短时间内接连学习时便会产生。联想干扰会导致概念混淆,妨碍记忆提取,并严重制约了能够同时有效掌握的知识主题数量,从而拖慢学习进程。为减轻联想干扰的影响,我们会尽可能将不相似的概念安排在同一时间学习,并将关联性强的知识点在时间上错开。这样做能够减少混淆,增强记忆提取效果,并有助于学生每天高效地同时学习多个知识主题。
最后,如果学生的诊断结果显示其存在某些基础知识薄弱环节,我们还会优化启动这些薄弱基础补习的时机。通常而言,相比于弥补基础知识的不足,学生对于学习他们已注册课程内的知识主题会抱有更大的热情——而当学生对自己所做的事情充满热情时,他们的学习效率和持续性往往也更高。因此,我们允许学生先从完成其注册课程中那些不依赖于其薄弱基础的知识主题入手。这有助于学生积累初步的学习动力,在主要学习目标上取得一定进展,并养成规律学习的习惯。一旦学生学习到某个阶段,必须先巩固薄弱基础才能在注册课程中继续前进时,他们此前积累的充足动力将有助于他们保持高昂的学习热情。
任务选择算法如何挑选需要复习的主题
如前所述,复习活动遵循间隔重复计划,旨在优化学生对所学知识的长时程记忆效果。然而,在挑选学习任务时,我们还会进行更深层次的优化,以求最大限度地减少复习次数。我们常常能够挑选出这样的任务:其附带的隐式重复练习足以「消除」掉其他主题中已到复习期限的内容(并顺延那些即将到期的复习)。
例如,如果一名学生同时有 一位数乘法、一位数与两位数加法 以及 两位数乘以一位数 这几个主题需要复习,那么他们仅需进行一次关于 两位数乘以一位数 的复习,便可一并完成所有这些复习任务。这是因为这次复习的效果会「涓滴」到另外两个被隐式练习到的主题。
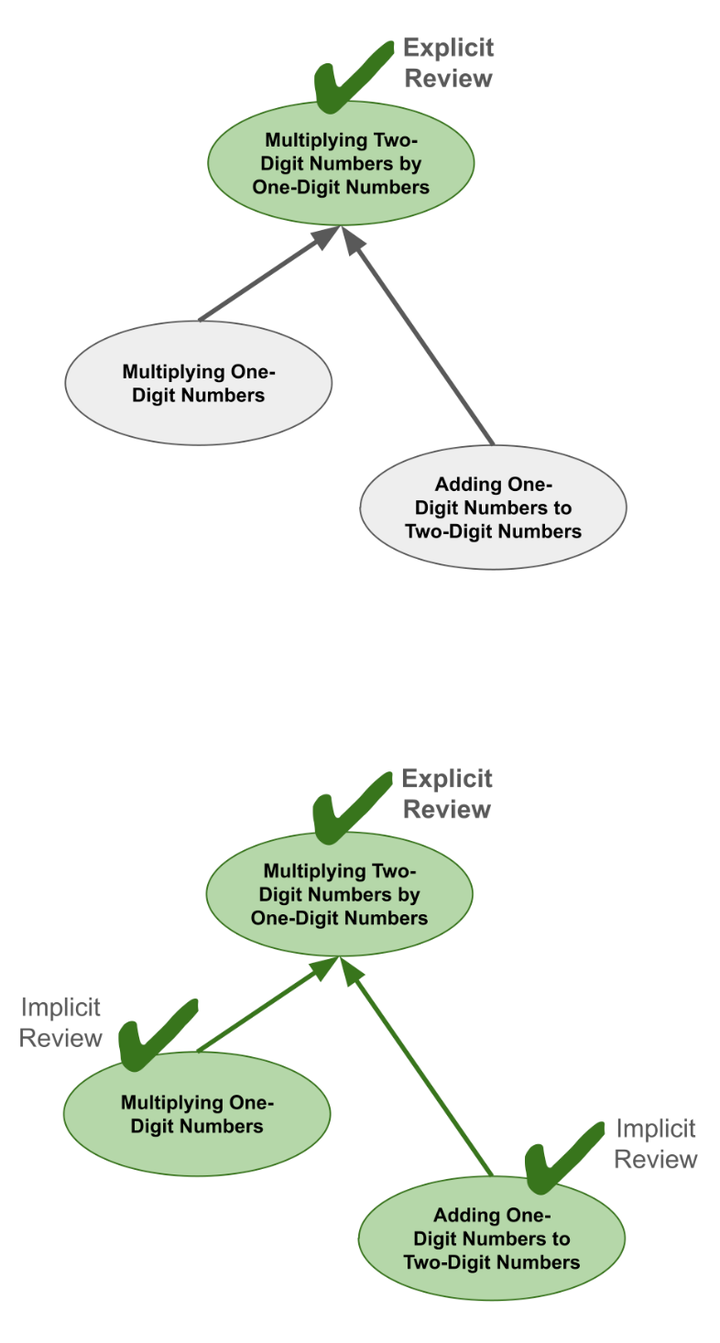
总而言之,每当学生有到期复习内容时,我们会将这些复习任务压缩整合到一个更为精简的学习任务组合中,确保这些任务能够隐式涵盖(即通过隐式练习的方式)所有这些到期复习内容。在条件允许的情况下,我们会通过安排新的课程学习来「消除」到期的复习任务,从而使学生能够在不实际拖慢新知识学习进度的前提下,完成必要的复习。我们将这一过程称为「重复压缩」,因为它能将尽可能多的间隔重复练习压缩到尽可能少的任务中去。这就好比用最少的推力,引发一整排多米诺骨牌的连锁倾倒。
间隔重复自然而然地催生了「交错复习」(亦称「混合练习」)。这是一种效果显著的复习策略,其核心在于将最小有效剂量的练习分散到各种不同的技能当中。交错练习与「集中练习」形成鲜明对比,后者是一种效率较低的方法,指的是对单一技能进行长时间的连续重复练习。集中练习容易使人产生虚假的掌握感和流畅感,因为它让学生习惯于机械地、不假思索地套用同一种解题方法来解决同一种类型的问题。与此不同,交错练习则创造了一种「合意困难」,这种困难能极大地促进知识的记忆保持和迁移泛化能力,使其成为一种更为高效的复习策略。
算法如何根据学习节奏进行自适应调整
前述讨论的所有算法都能够根据学生的学习节奏进行自适应调整。
我们的间隔重复算法能够针对每一位学生在每一个独立知识主题上的学习节奏进行调整。每位学生都有一个「学生-主题学习速度」指标,用以衡量该主题对于每位学生的个体难易程度,这个速度指标反映了每次复习所能达到的间隔重复效果。
- 例如,2x 的速度表明该主题对学生而言较为容易,学生将以两倍于标准值的速度推进其在该主题上的间隔重复进程,因为他们在这个特定主题上无需过于频繁的练习。
- 反之,0.5x 的速度则意味着该主题对学生而言更具挑战性,学生将以标准值一半的速度推进其间隔重复进程,因为他们在这个特定主题上需要更为频繁的练习。
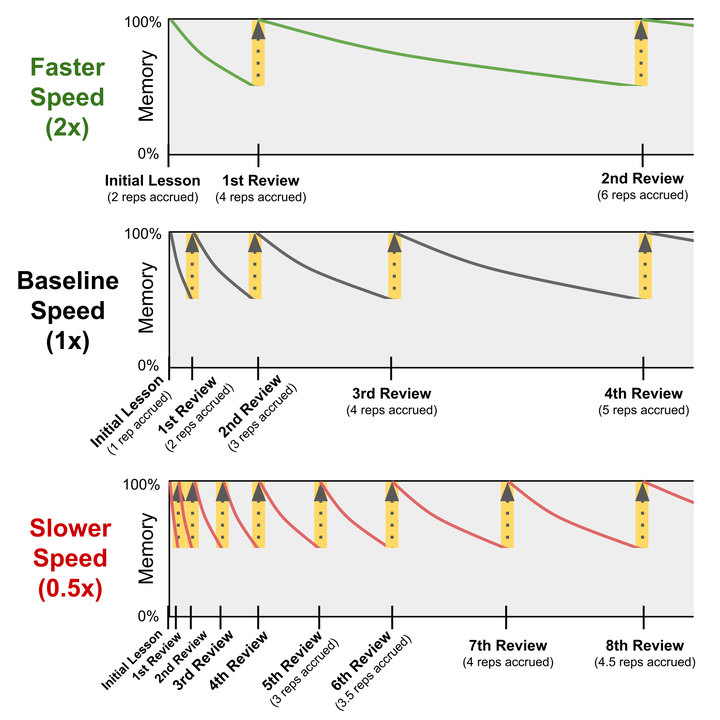
任务选择算法会进行更进一步的自适应调整:当系统评估某个主题对学生而言难度较大时,会强制学生进行显性复习(而不仅仅是通过隐式练习来完成复习)。我们为那些需要更多练习来消化和吸收那些隐式复习的较难知识点,并且需要更多辅助来理解和归纳「先前所学是当前所学内容的特例(或组成部分)」这一概念的学生,提供了这样的支持。
即便在单个学习任务内部,教学节奏也会根据学生的实际能力进行动态调整,相应加快或减慢。学生在学习任务中的答题正确率越高,他们为完成该任务所需回答的题目数量就越少。当学生答错题目时,我们会增加必需的题目数量,以便提供更多的练习机会、更多的学习契机以及更多展现学习成果的可能。
如果学生答错的题目过多,我们会暂停该课程的学习,因为让学生在困境中持续挣扎是对其时间的低效利用。在课程暂停期间,我们会引导学生先去学习其他不相关的知识主题并取得进展,之后再请他们重新尝试先前暂停的课程。通常情况下,稍作休息并换个思路,学生往往就能顺利克服困难。
然而,如果学生在重新尝试暂停的课程时再次受阻,且未能取得任何额外进展,那么我们会进一步放缓节奏,并为他们提供补救性复习,以帮助他们巩固与当前学习困境的核心症结最为相关的那些基础知识领域。我们的知识图谱会追踪记录在每节课程的各个部分中所运用到的关键前置知识,这使得我们能够精准定位到成功进行补救所必需的确切主题,即便这些主题在数学知识层级体系中可能处于较早的阶段。
针对测验环节,也设有相应的补救流程:每当学生在测验中答错一道题目,我们会放缓节奏,并立即针对相应的主题安排一次补救性复习。每次测验都包含一组从学生先前已学知识中随机抽取的多样化的主题组合,其中会优先选择学生当前注册课程中的主题,并适当降低那些以往测验中已出现过或已被其他可测验主题所包含的主题的优先级。其目标在于全面检验学生的知识掌握情况,检测出任何未曾预料到的薄弱环节,并帮助他们即时巩固这些领域。
为了进一步适应学生的学习节奏,在挑选测验题目时,我们还会根据学生的能力水平来调整题目难度,以期学生的平均得分能够达到 80% 左右。得分高于 80% 的学生,在下一次测验中将会遇到难度稍有提升的题目变式;而得分低于 80% 的学生,则会遇到难度略有降低的题目变式。实践证明,当测验既具有挑战性又不过于让学生感到难以承受时,其对于学习的价值才能最大化。
Thoughts Memo 汉化组译制
感谢主要译者 gemini-2.5-pro-exp,校对 Jarrett Ye
原文:Math Academy
