我们所有的课程内容全面,且严格遵循共同核心标准,通常涵盖数百个独立的知识点。每门课程都始于一场自适应诊断考试,旨在通过识别学生所欠缺的必备前置知识以及已掌握的课程内容,为其打造量身定制的学习体验。
官方权威认证
Math Academy 的数学课程已获得「西部学校和学院协会认证委员会」(Accrediting Commission for Schools, Western Association of Schools and Colleges)的全面认证。www.acswasc.org

Math Academy, LLC. 现已正式注册,并被收录于加州大学(UC)的《在线课程出版商名录》。你的家庭学校(home school)可以通过其 UC 课程管理门户,将我们的课程添加至学校的课程列表中,以便我们为你出具官方成绩单,用于申请有效的 UC a-g 学分。
小学阶段课程
我们的入门课程为四年级数学,是任何已掌握 12 以内乘法表并具备独立阅读能力的学生理想的起点。
四年级数学
学习多位数的加、减、乘、除运算。接触包括分数和小数在内的不同数字类型,并学习几何学中的线与角。
五年级数学
学习使用负数、分数和小数进行算术运算。解决涉及度量、数据和几何的实际应用问题。
预代数
本课程为小学算术与初中代数及几何之间搭建起一座桥梁。你将进一步深化对算术和几何的理解,学习变量知识,并求解线性方程、不等式及方程组。
预代数 vs. 6-8 年级数学
「预代数」课程涵盖了标准 6-8 年级数学课程的全部内容,但教学结构更为精炼紧凑。
高中课程
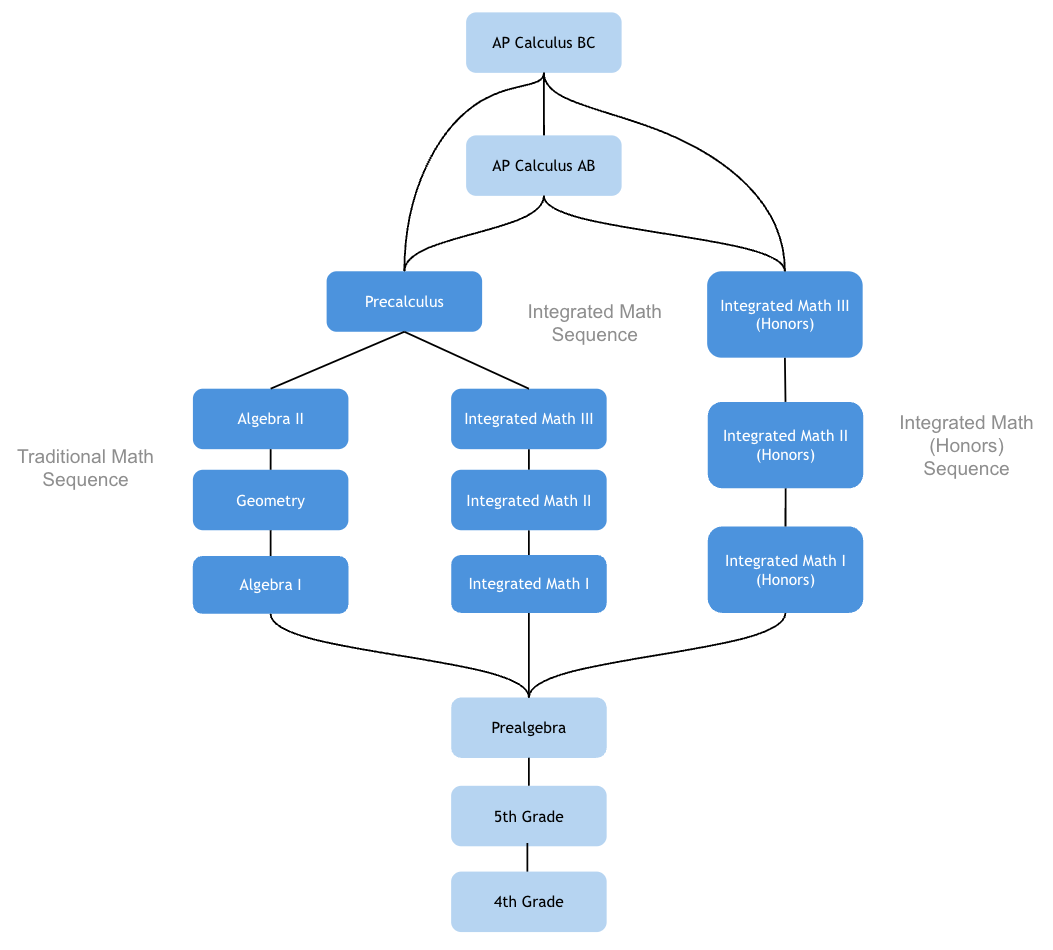
我们提供三种课程序列供你选择:传统数学序列、综合数学序列和综合数学(荣誉)序列。传统序列与综合序列所涵盖的知识点完全相同,区别仅在于部分主题的引入顺序有所不同。
传统序列一个公认的缺点是:学生在结束了一整年的几何课程学习后,往往需要在代数 II 课程中重新学习许多代数 I 的技能。(不过,我们的间隔重复算法能够让所有学过的技能时刻保持鲜活,因此在很大程度上缓解了这个问题。对于某些家庭而言,如果学生正在或将要就读的学校只提供传统课程,那么遵循传统序列可能会更加方便。)
而综合数学(荣誉)序列的进度则要快得多,仅用三年时间即可学完四年的数学内容。
传统数学序列
代数 I
让你的代数技能更上一层楼,学习函数与图形,并深入探索二次方程。
几何
学习计算各类物体的长度、面积和体积。探索直角三角形中角与边长之间的关系。
代数 II
精通包括二次方程、对数、三角函数等在内的高级函数代数。深入探索多项式理论。
预微积分
学习高等三角学以及概率与统计的核心概念。接触复数、向量和矩阵等高等数学的研究对象。
综合数学序列
综合数学 I
让你的代数技能更上一层楼,学习函数与图形,并解决几何与现实世界建模中的难题。
综合数学 II
精通二次方程的代数运算,并熟悉多项式、对数、三角函数等更高级的函数。学习概率论的核心概念。
综合数学 III
深入探索多项式代数,练习绘制三角函数图形,并精通根式函数和对数的代数运算。学习组合学、概率与统计的核心概念。
预微积分
学习高等三角学以及概率与统计的核心概念。接触复数、向量和矩阵等高等数学的研究对象。
综合数学(荣誉)序列
荣誉序列课程在三年内学完四年的高中数学内容(包含预微积分)。相比之下,标准的综合数学序列的终点与代数 II 水平相当,之后衔接预微积分。
综合数学 I(荣誉)
让你的代数技能更上一层楼,学习函数与图形,并解决几何与现实世界建模中的难题。
综合数学 II(荣誉)
精通包括二次方程、多项式、对数、三角函数等在内的高级函数代数。学习组合学、概率与统计的核心概念。
综合数学 III(荣誉)
深入探索多项式、根式函数、有理函数的代数运算,以及高等三角学。接触复数、向量、矩阵、参数方程和极坐标方程等高等数学的研究对象。
应试备考课程
备考课程帮助学生将学习重心聚焦于特定考试的内容,并精准提升关键应试技能,以取得个人最佳成绩。
SAT 数学基础
涵盖所有 SAT 指定考点,例如初等和高等代数、二维和三维几何、三角学、函数、统计学、概率论以及解题技巧。
ACT 数学 即将推出……
掌握 ACT 的重要考点,包括但不限于:实数与复数、整数与有理数指数、向量与矩阵、线性、多项式、根式和指数关系,以及线性、根式、分段、多项式和对数函数、几何、统计学与概率论。
AP 课程
AP 微积分 AB 和 AP 微积分 BC 是高中大学预修课程,旨在帮助学生备战大学理事会(College Board)举办的相应 AP 考试。AP 微积分 BC 的内容相当于大学两个学期的微积分课程(即微积分 I 和微积分 II),而 AP 微积分 AB 的内容覆盖面稍窄,约为此内容的 70%。
AP 微积分 AB
学习极限、连续性、导数、不定积分和定积分,并学会在各种情境中灵活应用这些概念。
AP 微积分 BC
精通单变量微积分的基础知识,包括向量、参数方程和极坐标方程。学习应用收敛性判别法于无穷级数,并运用泰勒级数来近似函数。
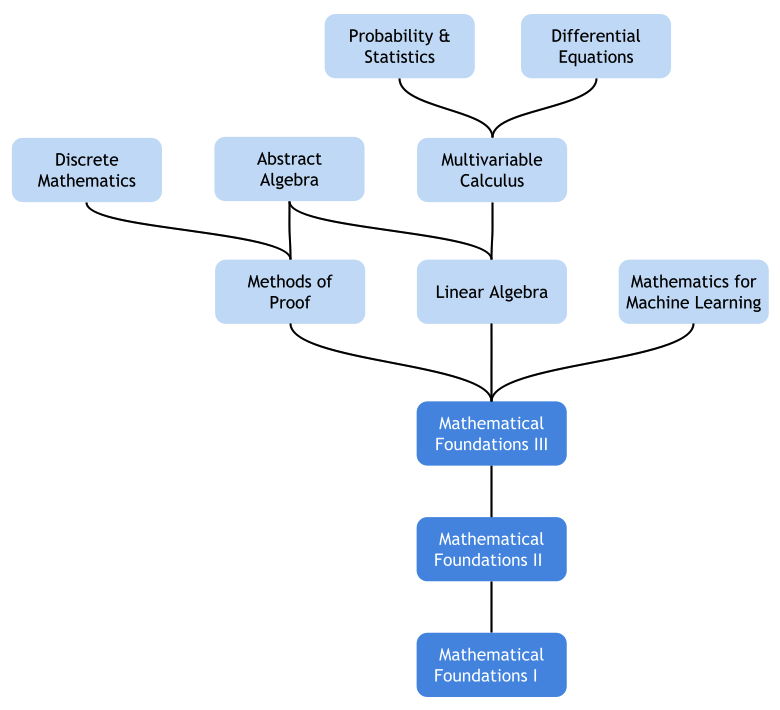
数学基础课程
「数学基础」序列专为希望攻读高等院校课程但缺乏必备基础知识的成年学习者设计。无论你是想从零开始,还是只想巩固微积分知识,这都将是你迎头赶上、夯实基础的最快、最有效途径。
数学基础 I
巩固你的算术能力,学习变量与图形,提升你的代数水平,并掌握几何学精髓。
数学基础 II
精通包括二次方程、对数和三角函数在内的高级函数代数。深入探索多项式理论,学习微积分中的极限、导数和积分基础,并探索复数、向量、概率和统计等高等数学概念。
数学基础 III
学习计算极限、导数和积分的高等微积分技巧,并应用微积分解决相关变化率、最优化、质点运动和微分方程等问题。更深入地探索复数、向量、矩阵、参数曲线、极坐标曲线、概率与统计。
大学课程
我们的大学课程以顶尖大学严谨的学期制课程为蓝本,并在许多方面有所超越。这些课程内容全面,涵盖了相应学科在本科阶段理应包含的每一个主要课题。
微积分 I
学习作为现代科学与工程基石的「变化」的数学。精通极限、导数与积分基础。
微积分 II
深化你对微积分的理解:掌握高等积分技巧,运用微分方程为真实世界建模,以及更多内容。
线性代数
深入探索向量与矩阵背后的数学原理。学习各种计算方法和概念联系,并将其融合成一个优美的理论整体。
多元微积分
将你对微积分的理解拓展至向量值函数和多变量函数。
证明方法
熟练掌握集合与逻辑——数学中最基本的结构与运算。了解证明的本质,并精通证明数学命题的各种技巧。
离散数学
学习对离散量(而非连续量)进行推理的数学技巧。接触在计算机科学领域应用广泛的图论、算法及其他数学分支。
概率与统计
学习关于「或然率」的数学,并运用它对不确定事件的可能结果做出精确推断。运用严谨的数学方法分析真实世界的数据。
机器学习数学
学习理解和实现核心机器学习算法所必需的线性代数、多元微积分、概率与统计的关键技能和核心概念。本课程将为你攻读大学水平的机器学习课程做好准备,这些课程涵盖梯度下降、神经网络与反向传播、支持向量机、线性回归的扩展(如逻辑回归和套索回归)、朴素贝叶斯分类器、主成分分析、矩阵分解方法以及高斯混合模型等主题。
微分方程 即将推出……
掌握多种技巧,以解决在运用微积分对真实世界情境建模时产生的各类方程。
抽象代数 即将推出……
深入探索支配数学对象之间相互作用的核心关系。学习识别代数结构,并运用数学推理得出普适性结论。
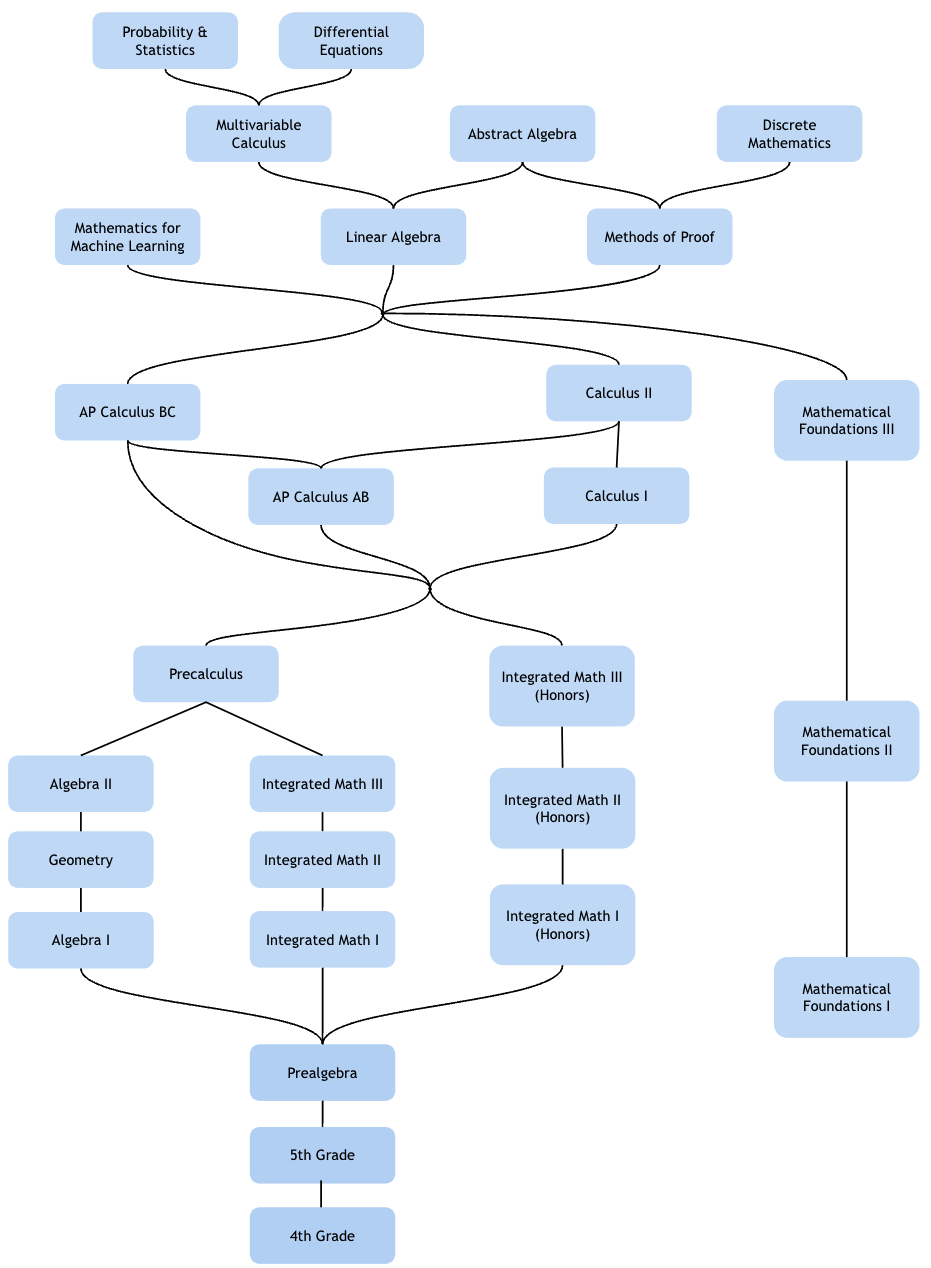
体系完备的课程
我们丰富的课程目录涵盖了从初等算术到大学高年级数学的全部内容,以及其间所有过渡阶段的知识。
Thoughts Memo 汉化组译制
感谢主要译者 gemini-2.5-pro,校对 Jarrett Ye
原文:Courses

