总目录:0 目录《间隔重复的历史》
本文主要介绍 SM-4 和 SM-5,由于内容实在太长了,这里拆成上中下三篇。
上篇主要讲 SM-4 为啥被提出、实际效果如何、带来哪些启发。
引入弹性间隔函数
SuperMemo 2 很棒。它的简单算法已经在流行的应用程序(如Anki或Mnemosyne)中存活至今。然而,该算法是愚蠢的,因为其没有办法修改最优间隔的函数。1985 的发现是板上钉钉的。记忆复杂度和稳定性增加用相同的数字表示:E-factor。这有点像在自行车上使用同一个控制杆来改变档位和方向。
单个的项目可以根据其估计的难度来调整复习的间隔。这些变化可以补偿最优间隔函数中的错误。即使算法收敛速度慢,理论上也是收敛的。主要的缺陷是,在算法 SM-2 中,新项目不会从旧项目的经验中受益。
算法 SM-4 是第一次尝试用通用的适应性武装 SuperMemo。它于 1989 年 2 月竣工。最后,适应性表现得太慢了,但是用算法 SM-4 收集的灵感对于进一步发展是至关重要的,特别是在理解间隔重复中的稳定性与准确性问题上。简而言之,SM-4 算法太过稳定而不能准确。这在 7 个月后的 SM-5 算法中很快得到了纠正。以下是我的硕士论文的一段摘录。
档案警告:为什么使用文字档案?
本文是 Piotr Wozniak 的《优化学习》(1990)的一部分。
算法 SM-2 的主要错误似乎是最优间隔函数的任意形状。虽然在实践中非常有效,并且经过多年的实验重复得到了证实,但是这个函数并不能被科学地证明其有效性,也不能检测出最优间隔的几天变化对学习过程的整体影响。考虑到这些缺陷,我决定使用常规的 SuperMemo 重复来验证最优间隔的作用!
使用那些在寻找E因子时应用的优化过程,我想让程序在任何时候修正最初提出的函数,只要修正看起来是合理的。
为了达到这个目的,我把最优间隔的函数列成表。

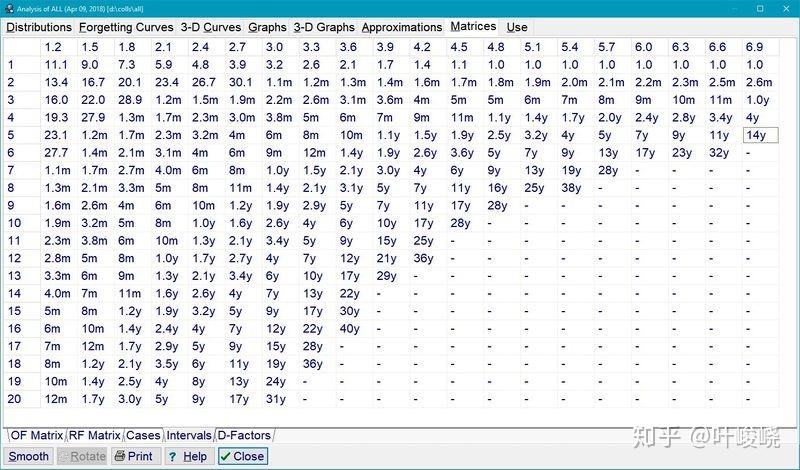
图:最优间隔矩阵出现在1989年的SuperMemo 4中,并在SuperMemo 17中保留至今,几乎没有变化。在SuperMemo 4中,它是优化间距的信息来源。在SuperMemo 17中,它是由算法SM-15生成的矩阵得到的,同时与算法SM-17使用。这幅图展示了一个来自SuperMemo 5的矩阵,并显示了与原始矩阵值的显著偏离。在SuperMemo 4中,改编的速度要慢得多
最优间隔矩阵(后来称为 OI 矩阵)的初始项最初取自算法 SM-2 中的公式。
SuperMemo 4(1989 年 2 月)实现了新的解决方案,使用OI矩阵来确定重复间隔的值:
I(n):=OI(n,EF)
上式中:
- I(n) - 给定项目的第n次重复间隔(以天为单位),
- EF - 项目的E-Factor,
- OI(n,EF) - OI矩阵中对应第 n 次重复和 EF 的项目。
然而,OI 矩阵并不是固定的。在重复的过程中,矩阵的具体项随着分数的不同而增加或减少。例如,如果项目指出最优的间隔是 X,使用的间隔是 X+Y,而这个间隔之后的等级不低于 4,那么项目的新值将落在 X 和 X+Y 之间。
因此,处于平衡状态的 OI 项的值应该稳定在一个点上,在这个点上,低保留项流与高保留项流对矩阵的影响相平衡。
因此,SuperMemo 4 试图给出最优间隔函数的最终定义。
刚性 SuperMemo 4
我很快就意识到新算法的验证-校正周期太长了。这与在计算机上运行 1985 年实验没有太大的不同。为了确定十年的间隔,我需要十年的时间来测试审查的结果。这导致了七个月后的 算法 SM-5。以下是我在硕士论文中描述的算法 SM-4 的问题:
档案警告:为什么使用文字档案?
本文是 Piotr Wozniak 的《优化学习》(1990)的一部分。
算法 SM-4 在 SuperMemo 4 中实现,并在 1989 年 3 月9 日至 1989 年 10 月 17 日期间使用。虽然修改最优间隔函数的主要概念似乎是向前迈出的一大步,但是算法的实现是失败的。该算法的基本不足似乎源于在修改OI矩阵时应用的公式。
有两个最明显的缺陷:
- 修改太过细微,无法在合理的短时间内明显地重新排列 OI 矩阵,
- 对于较长的间隔重复时间,修改的效果需要很长时间才能稳定固定,即需要很长时间才能看到几个月间隔修改的结果,并在必要时进行修正
在使用 SM-4 算法 7 个月后,特定数据库的 OI 矩阵与它们的初始状态并没有太大的不同。人们可以用我早先关于最优重复间隔真值的预测的正确性来解释这一事实,然而,正如后来用算法SM-5证明的那样,矩阵稳定的实际原因是优化公式中的缺陷。
就获取率和保留率而言,没有可靠的证据表明 SM-4 算法带来了任何进展。轻微的改进也可能与软件的总体改进和项目制定原则的改进有关。
SuperMemo4 的残余在新的 SuperMemo 里
有趣的是,你仍然可以在新版本的 SuperMemo 中看到最优间隔矩阵。这个矩阵并没有被算法使用,但是它显示在SuperMemo 统计数据中,因为它告诉用户复杂性对学习过程中项目的前景的影响。
如果你比较一个使用了 8 个月的 SuperMemo 5 生成的矩阵,你会发现它与使用了 20 年的算法 SM-8 生成的矩阵有显著的相似性:
图片:算法 SM-17 不再使用最优间隔矩阵。但是,仍然可以通过算法 SM-15 的步骤来生成。这些列与以A因子表示的材料的简易度相一致。这些行对应于以重复类别表示的记忆稳定性
算法SM-4
以下是我在硕士论文中描述的算法SM-4的概要:
档案警告:为什么使用文字档案?
本文是 Piotr Wozniak(1990) 的《优化学习》的一部分。
算法 SM-4 在 SuperMemo4.0 中的应用
- 算法
- 将知识分解为最小的卡片
- 所有卡片的 EF 设置为 2.5
- 列出以重复次数和 EF 为索引的 OI 矩阵
- 使用下面的重复间隔来初始化 OI 矩阵:
- OI(1,EF)=1
- OI(2,EF)=6
- for n>2 OI(n,EF)=OI(n-1,EF)*EF
- OI(n,EF) - 难度为 EF 的卡片在第 n 次复习时的最优间隔
- 使用 OI 矩阵来确定重复间隔:
- I(n, EF) = OI(n, EF)
- I(n, EF) - 难度为 EF 的卡片在第 n 次复习时的间隔
- OI(n, EF) - OI 矩阵对应 n 和 EF 的值
- 每次重复后都用 0-5 的成绩来给回忆质量打分
- 每次重复后都根据下列公式修改 EF:
- EF' - EF 的新值
- EF - EF 的旧值
- q - 回忆质量打分
- 如果 EF < 1.3 则令 EF = 1.3
- 每次重复后都修改 OI 矩阵上的相关项
- 一个示例公式如下(SM-4 中实际使用的公式更复杂):
- OI - OI 对应项的旧值
- OI' - 计算 OI 对应项新值的辅助值
- OI'' - OI 对应项的新值
- interval - 之前的间隔
- fraction - 调和参数
- EF - 重复卡片的 EF
- q - 回忆质量评分
- 注意,当 q = 4 时 OI 不会改变,当 q = 5 时 OI 增长是 q = 0 时减少的 4 分之一
- 如果回忆质量小于 3,卡片重新开始复习,并且不改变其 EF
- 在某一天的每次重复练习之后,再重复那些在回忆质量评分中得分低于4分的卡片。继续重复,直到所有这些卡片得分至少4分。
间隔矩阵的问题
SM-4 表明,除了收敛速度慢以外,使用间隔矩阵会导致一些问题,而用 OF 来替换间隔可以很容易解决。这些额外的缺陷使 SM-5 快速实现。以下是使用最优间隔矩阵的缺陷:
档案警告:为什么使用文字档案?
本文是Piotr Wozniak(1990)的《优化学习》的一部分。
- 在重复过程中,可能会发生一个间隔在计算后短与前一个间隔的情况,这与 SuperMemo 的假设不一致。此外,即使可以通过不允许间隔增加或减少超过某值来避免这种情况,但这会极大减慢矩阵的优化过程。
- 特定卡片的 EF 会不断修改,因此在 OI 矩阵中,一个卡片可以从一个难度类别转移到另一个难度类别。如果卡片重复的次数足够大,将会导致卡片重复过程的严重影响。注意,卡片连续重复次数越大,相邻的 EF 列的最优间隔间的差异就越大。英雌,如果 EF 增加,卡片的最优间隔会变得不自然的长,在相反的情况下间隔可能会变得太短。
SM-4 尝试将最优间隔的长度和重复次数相关联。这种方法似乎是不正确的。因为记忆对之前使用的重复间隔长度更敏感,而不是重复次数。
下一章:06 1989: SuperMemo 适应用户记忆(中)

