总目录:0 目录《间隔重复的历史》
上一章:06 1989: SuperMemo 适应用户记忆(中)
下篇主要从数据和理论上证明了 SM-5 算法对 SM-2 算法的优越性。本来还有后续的算法优化内容,介于其过于硬核,就不搬到知乎上了,感兴趣的朋友可以直接看我的电子书:
间隔重复的历史SuperMemo5 的评估(1989)
SuperMemo 5的优势如此明显,以至于我没有收集太多数据来证明我的观点。我只拿我的硕士论文做了几次比较,结果毫无疑问。
档案警告:为什么使用文字档案?
本文是Piotr Wozniak(1990)的《优化学习》的一部分。
3.8. 算法 SM-5 的评估
算法 SM-5 自 1989 年 10 月 17 日开始使用,它提供了一种确定理想的最优间隔函数的有效方法,超出了所有人的预期,从而提高了习得率(在 9 个月内学习了 15,000 个项目)。图 3.5 显示习得速率至少是组合应用 SM-2 和 SM-4 算法的两倍!
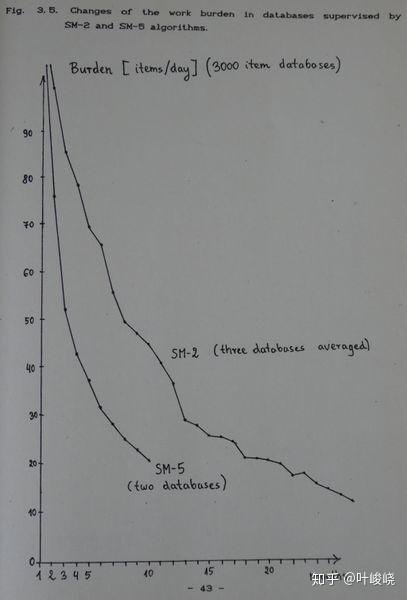
图片:在 SM-2 和 SM-5 算法的监督下,数据库中工作负担的变化
对于 10 个月的数据库,知识保留率提高到 96% 左右。下面列出了选定数据库中的一些知识保留率数据,以显示 SM-2 和 SM-5 算法之间的比较:
- 日期 - 测量日期,
- 数据库 - 数据库的名称;ALL 表示所有数据库的平均值
- 间隔 - 数据库中项目使用的平均当前间隔
- 保留率 - 数据库中的知识保留率
- 版本 - 数据库所应用的算法版本
| 日期 | 数据库 | 间隔 | 保留率 | 版本 |
|---|---|---|---|---|
| Dec 88 | EVD | 17 days | 81% | SM-2 |
| Dec 89 | EVG | 19 days | 82% | SM-5 |
| Dec 88 | EVC | 41 days | 95% | SM-2 |
| Dec 89 | EVF | 47 days | 95% | SM-5 |
| Dec 88 | ALL | 86 days | 89% | SM-2 |
| Dec 89 | ALL | 190 days | 92% | SM-2, SM-4 and SM-5 |
在复习过程中,记录了下列成绩分布情况:
| Quality | Fraction |
|---|---|
| 0 | 0% |
| 1 | 0% |
| 2 | 11% |
| 3 | 18% |
| 4 | 26% |
| 5 | 45% |
根据算法 SM-5 的假设,该分布产生的平均回忆质量等于 4。遗忘指数等于 11%(成绩低于 3 的项目被认为是被遗忘的)。请注意,保留率数据表明数据库中只有 4% 的项目没有被记住。因此,遗忘指数超过遗忘项目百分比的 2.7 倍。
在一个 7 个月前的数据库中,发现 70% 的项目在测量之前的重复过程中甚至没有忘记一次,而只有 2% 的项目遗忘次数超过 3 次
新算法优越性的理论证明
Anki 对 SuperMemo 5 的批评需要根据现代的间隔重复理论来做一个简单的证明。我们可以表明,今天的记忆模型可以映射到两种算法基础上的模型:算法 SM-2 和算法 SM-5,两者之间的关键区别是最优间隔函数的适应性缺失(在算法SM-5中由最优因子矩阵表示)。
SInc = f (C、S、R) 是一个稳定性增长函数,复杂性 C、稳定 S、可恢复性 R 作为参数。这个函数决定了最优学习中复习间隔的递增。
两种算法,SM-2 和 SM-5 都忽略了可提取性维度。理论上,如果两种算法都能完美运行,我们可以假设它们的目标是 R=0.9。正如可以在 SuperMemo 中测量的那样,这两种算法都失败了,因为它们不知道相关的遗忘曲线。他们只是不收集遗忘曲线数据。这种数据收集的可能性是在 1991 年才在算法 SM-6 中引入的。
然而,如果我们假设 1985 和 1987 启发式是完美的猜测,在理论上,该算法可以使用SInc=F(C,S),常数R为90%。
由于 SM-2 使用相同的数字 EF 用于稳定性增加和项目复杂性,对于 SM-2,我们有以 EF=f'(EF,interval) 的形式表示的 SInc=f(C,S) 方程,其中的数据可以很容易地显示 f<>f' 。令人惊讶的是,SM-2 中使用的启发式通过解耦 EF 和项目复杂性之间的实际联系,使这个函数发挥作用。由于数据显示 SInc 随着 S 的增加而不断减少,在算法 SM-2 中,根据定义,如果要用 EF 来表示项的复杂度,那么所有项都需要在每次复习时获得复杂度。在实际应用中,算法 SM-2 使用 EF=f'(EF,interval),即 SInc(n)=f(SInc(n-1),interval)。
让我们假设 EF=f(EF,interval) 启发式正如 SM-2 算法的支持者所声称的那样,是一个很好的猜想。令 SInc 在算法 SM-5 中由 O-factor 表示。然后我们可以将 SInc=f(C,S) 表示为 OF=f(EF,interval)。
对于算法 SM-2, OF 是常数,等于 EF,在算法 SM-5 中,OF是可适应的,可以根据算法的表现进行修改。很明显,对表现差的算法进行惩罚,降低OF 矩阵对应的项,并通过增加对应的项来奖励它,这要优于保持不变。
有趣的是,尽管 SM-2 算法的支持者声称它表现得很好,但神经网络 SuperMemo 算法的支持者却不断指责代数算法:缺乏适应性。实际上,算法 SM-17 的适应性是最好的,因为它是基于最精确的记忆模型。
可以想象,在 SM-2 中使用的启发法是如此精确,以致于原来对 OF=f(EF,interval) 的猜测不需要修改。然而,正如在实际应用中所显示的那样,OF 矩阵迅速发展,并收敛到这篇出版物(Wozniak, Gorzelanczyk 1994)中描述的值。它们与算法 SM-2 中的假设有本质上的不同。
总结:
- sm17 (2016): SInc=f(C,S,R), 3 个变量,f 是有适应性的
- sm5 (1989): SInc=f(C,S,0.9), 2 个变量,f 是有适应性的
- sm2 (1987): SInc=f(SInc,S,0.9) - 1 个变量,f 是固定的
从这篇开始,SuperMemo 的算法会越来越精致,也越来越硬核,所以不会翻译的太详细,想了解的朋友可以把我的翻译当作参考,具体细节还请看英文原文。
下一章:07 1990:记忆的通用公式