怎样用 Anki 理解公式：以统计学为例

最近我在对 Anki 知识库进行双周设计审查^[1]时，发现了这样一张需要重构的卡片：

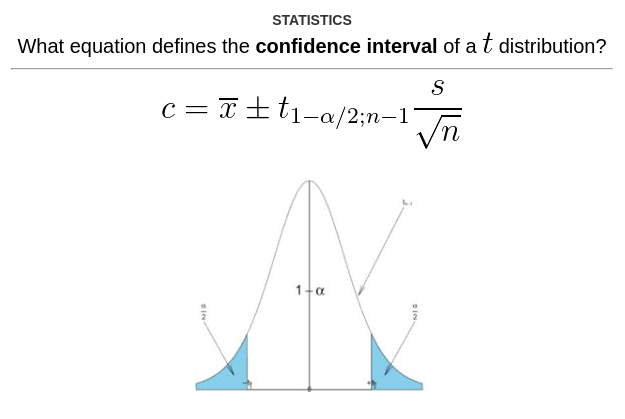
离我做这张卡大约有一年半了。它的简易度是 205%，就是说我一直没弄错。它的间隔是一年半，所以我短时间内不用再主动回忆他了。根据这些数据，这张抽认卡制作得挺成功。而且它是有用的：我制作这张卡片是因为我偶尔需要用 R 或 Python 计算并可视化数据的置信区间，知道卡片中的方程式后，我在 Google 上搜索正确的语法便能更快，更省脑力。

但是这张卡片有浓厚的卡片设计异味：我是通过死记硬背来记住这个方程的，这意味着我不能解释「为什么」这个方程的形式是这样的，因而回忆起来很困难，复习起来不愉快（即使我能答对），我现实生活中需要这些知识时，更是难以推理解释。

我隐约意识到这与 t-分布的临界值有关，但是当统计课程一结课，所有的知识很快变得非常模糊。

识别这样卡片的基本方法，是根据答错一张卡片的时候，你脑海里产生的想法：

• 如果我是把高质量的卡片弄错了，就会一激灵「噢，那确实，我懂了。我真傻。」
• 如果答错了死记硬背的卡片，我反而会想：「噢，真不走运。下次再试试吧。」
  

一般说来，通过死记硬背来学习公式在 Anki 是有风险的。公式的用意在于浓缩大量非常复杂的逻辑——通常是一整段的内容——而只用很小的空间。公式内在的复杂逻辑需要多张抽认卡才能加深理解。

所以让我们来优化好这张卡吧。我们将遵循分为两部分的策略，这也是我在科学类话题中经常使用的：

1. 识别出地标概念，便于让直觉有定位，然后
2. 围绕这些地标概念，添加足够必要的细节卡片。

大局地标概念

掌握统计问题背后的直觉是很棘手的，因为统计学充满了技术用语和准确假设，而统计学文本对此不假思索地使用。像总体、样本均值、标准误差、标准差和分布这样的术语很快就会互相混淆（我们甚至还没说区分 P.D.F.、P.M.F.、C.D.F.、P.P.F. 和 I.S.F. 这回事呢）

等等，我们在干啥？我的教授曾面向我们这帮计算机科学学生（哈！），像西西弗一样徒劳地教一些可靠的实验方法，而其中我依稀记得，任何数据样本的均值很神奇地遵循不错的理论分布（即使数据本身没有遵循这个分布）。这正是我们能够计算置信区间的出发点。但要我解释这个事实就很难了。

于是请谷歌图片来帮忙 (这里是原始图片来源)。 我缺少的概念抓手^[2]是抽样分布。一般说来，用图像来概括这样的概念要比用文本解释容易得多，所以我经常依靠图像给出问题的答案：

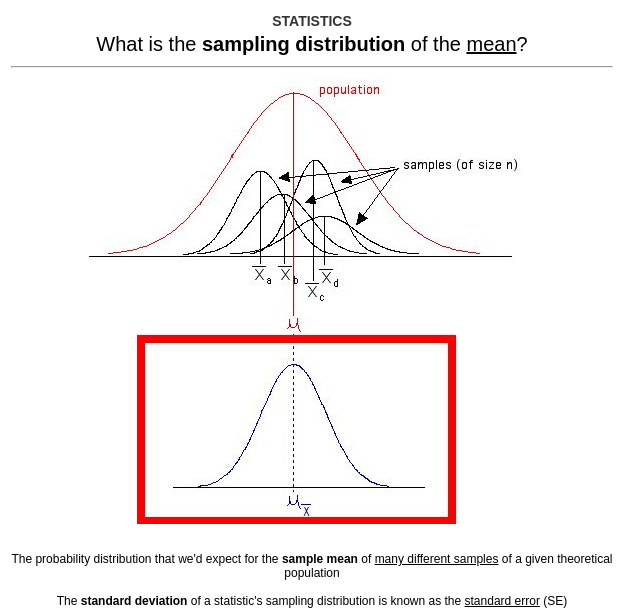
在我们的脑内文库中刻印下这张图片后（这也就是为什么概念抓手^[2]和技术用语威力无穷），我们就为记住置信区间做了更足的准备。仅仅是清晰而轻松地回忆起置信区间来自这样的分布函数，就已经很有用了。

但在我们继续前，我们可以再往地标概念上添一笔：

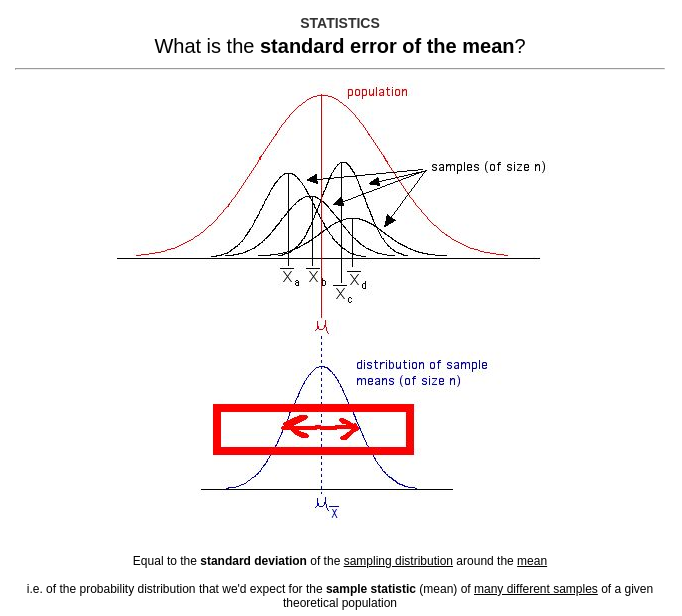
太棒了。我们已经解决地标概念了——该处理细节了！

细节卡

就像任何复杂的概念一样，为了用 Anki 学好公式，我们便要将其拆分，逐个击破。

对于公式，我会做卡来处理公式的每一项或者每一个符号。这样每个部分就成为自身的概念抓手：

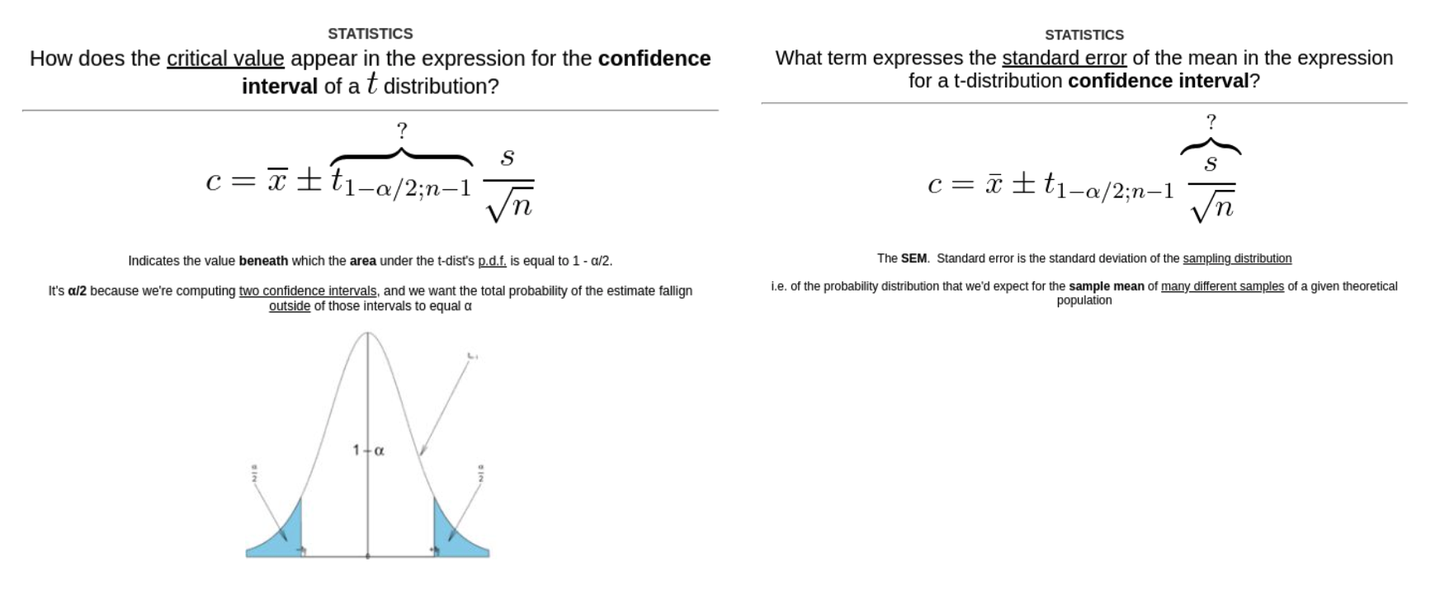
这真的很棒，因为比起原来放上一整个公式的卡片，现在的一张张卡片更能让我专注。例如，现在我可以慢慢考虑那个复杂的 1-α/2;n-1 下标 (也是公式中最难记住的部分)。

然而，公式中每一项还是很复杂，而且我们仍然在死记硬背。让我们再次对这两个问题发起挑战：

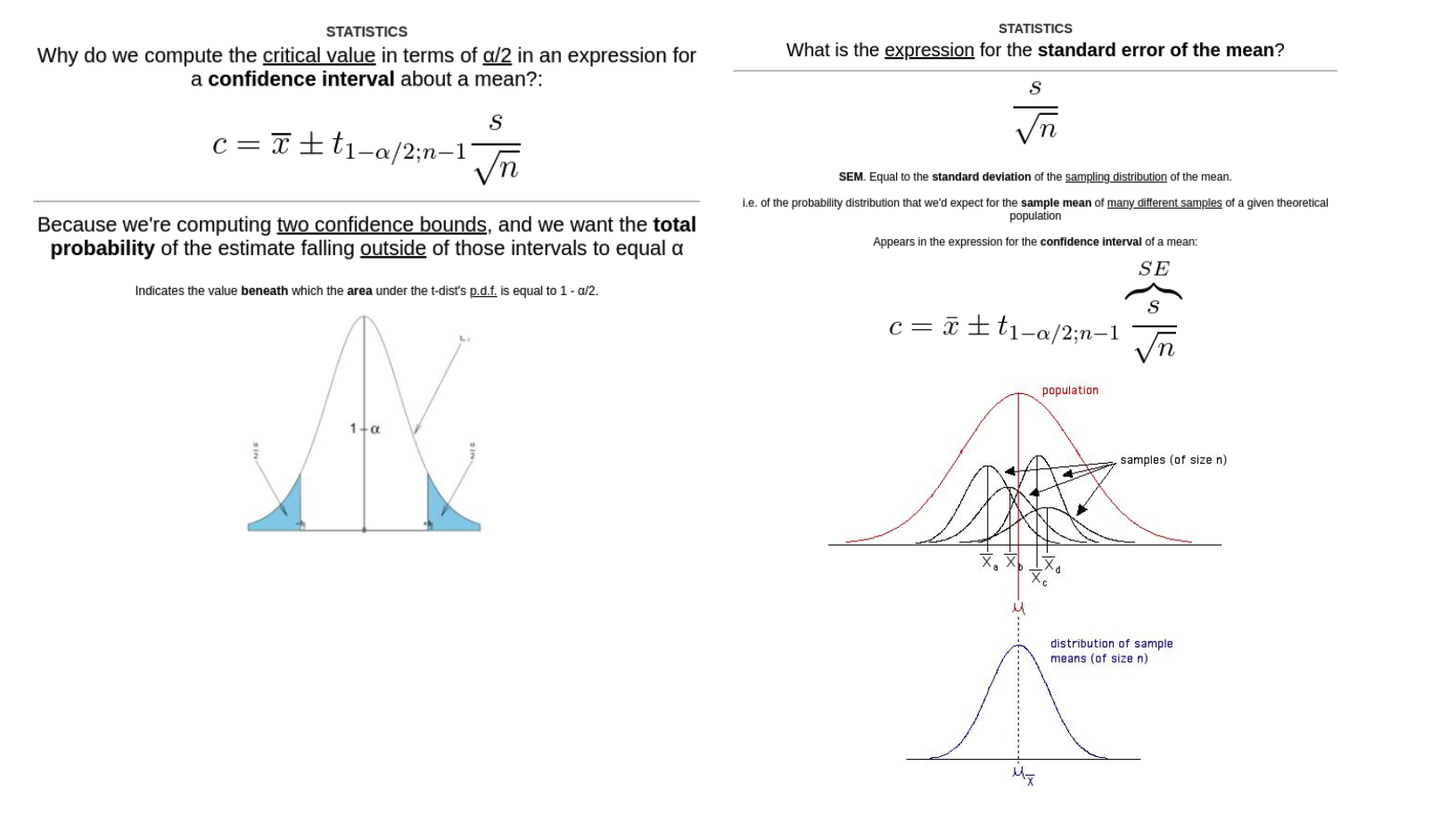
现在我准备好解释置信区间方程式的每一部分从何而来了，这个公式就更容易记住了。但更重要的是，推理也变得更容易，因为我比以前更多地依赖语义直觉，而不是死记硬背。

但要想让这张语义联系的网发展成更大的知识库，更具深度 (「为什么平均值的标准差随着 n 的平方根增大而减小？」) 或广度 (「什么时候使用 t-分布 而不是 z-分布 来计算关于某个平均值的置信区间？」) ，就不能停留在我们目前做的这几张卡片了。但是目标已经达成了：我们已经重构了一张卡片，所以设计审查可以告一段落了（好吧，说实话，这次设计审查花了我整整两天。有些重构任务一口气做不完啊！）

我只想加几张缩写卡片来巩固我新制作的概念抓手，然后就收工了：

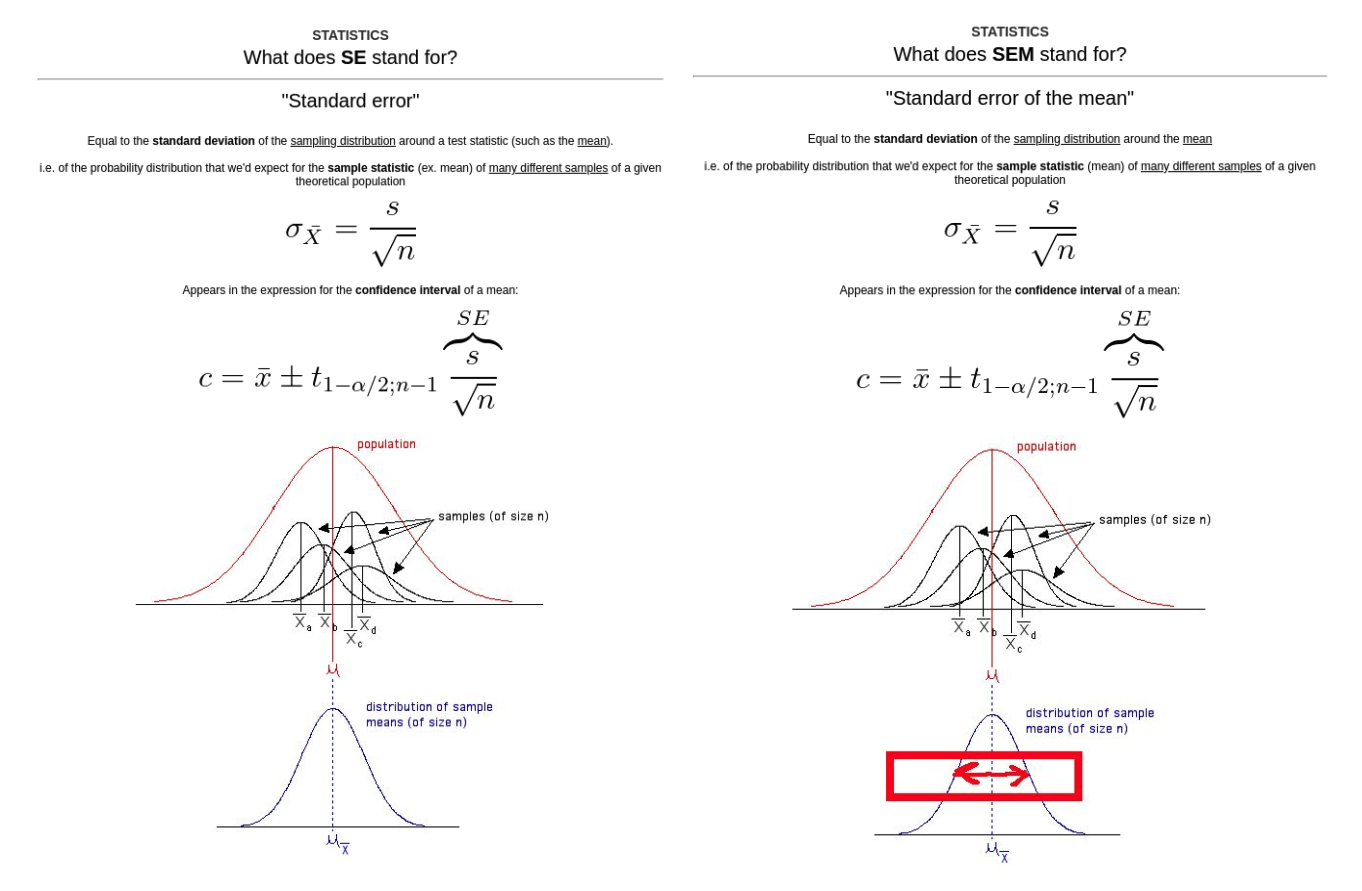
如果你好奇，这个案例里我保留了原来的卡片。保留完整公式的卡挺好，只需要一些支持性的分析卡片即可。所有这些卡片加在一起的记忆效果，远胜任何一张单独的卡片。

Thoughts Memo 汉化组译制
原文：Anki Design Study: Learning Statistics

更多有关制卡原则的内容，请关注：

← 返回目录