你不会因为钻研智商测试或者拉小提琴而变得更聪明,Dual n-back 训练也大概不会提升你的工作记忆。但你可以通过间隔重复[1]记住你想记住的任何东西。
间隔重复,无疑是我迄今为止使用过的最有效的认知技巧。曾经,我读过一本书后几乎什么都记不住。有时我会用 Kindle 标注重点,或者做些笔记,但从不复习它们。我曾天真地希望,即便我不能准确地说出我记住的内容(毕竟谁的记忆里是有索引的呢?),但重要的信息也能不知不觉地融入了我的知识体系,成为隐性知识。然而,这种想法大多只是自我安慰罢了。
我热爱学习,而间隔重复极大地提升了我的学习效果。然而,掌握这种方法的精髓并非一朝一夕之事。尽管网上充斥着大量如何高效应用间隔重复的建议,但这些建议往往停留在宏观原则层面,鲜少涉及具体实例。实际上,学习者最常遇到的困惑是:如何将一个具体而明确的知识点恰当地转化为一组抽认卡?
这篇文章描述了我用来撰写有效的抽认卡的规则,并尽可能提供了许多合理的例子。
间隔重复概述
这个想法在操作上非常简单:当你学习新知识时,你会制作抽认卡,每张卡片都包含一个问题和对应的答案。随后进行复习:先看卡片正面的问题,尝试回忆答案,再翻到背面查看正确答案。最后进行自我评分:判断你的回忆是否准确。
如果你一直回忆正确,那么你的复习间隔就会越来越长;反之则越来越短。
有些人使用纸质卡片,而大多数人则使用像 Anki 这样的软件,因为其算法能高效地安排复习,避免对材料过度复习。除非你特别偏爱纸质材料,否则建议选择软件。
限制因素
如果间隔重复真的如此高效,为什么它还没有像喝咖啡那样普遍?就像说:你这么聪明,为啥没有变富呢?
间隔重复的有效实践主要受到两个因素的限制。
习惯养成
间隔重复要发挥作用,关键在于将其转化为日常习惯。比如,我把抽认卡复习作为每天早晨例行活动的一部分。然而,养成新习惯本身就是一个挑战,对于患有注意力缺陷多动障碍(ADHD)或缺乏自律性的人来说,这个过程可能更为艰难。
每天坚持复习的必要性源于间隔重复算法的工作机制。这个算法会自动为你安排复习计划,免去了手动安排的麻烦。然而,只有在打开应用程序时,你才能知道当天需要复习哪些卡片。如果某天漏掉了复习,未复习的卡片会累积到下一天,增加次日的复习量。
一种常见的失败模式(我在熟练使用之前也多次陷入这种情况)是:使用 Anki 两周后中断,半年后重新拾起时发现积累了 600 张待复习的卡片。这种情况不仅打击学习积极性,更违背了间隔重复的核心原则——按照算法设定的最佳时间间隔进行复习。
对于这种情况,我能给出的建议有限。但如果你长期存在自律性不足的问题,或有未经治疗的注意力缺陷多动障碍(ADHD)等情况,那么在开始使用间隔重复法之前,最好先着手解决这些问题。
卡片的编写技巧
制作有效的抽认卡是一门需要时间习得的技巧。在我开始系统性使用间隔重复法的头四到六个月里,制作的大部分卡片事实上都不太实用,这种情况可能会让人感到沮丧。撰写这篇文章的主要目的是分享我的经验,希望能帮助你从一开始就能有效地运用间隔重复。
其中一个令人沮丧的原因是,在最初几周内(当你高频率地复习卡片时),你通常会记得这些抽认卡片,但几个月后,你开始回忆失败。它没有在你的长期记忆中扎根,因为在某种程度上写得不好。这种长周期的反馈意味着你需要一定的时间来通过试错来学习这些技巧。
鼓励的话
学习是一种自动、本能的过程,是智力的基本特征。学校教育如此糟糕,以至于人们认为必须拥有特殊类型的大脑才能有效学习,而且「学习」这个概念会引起人们的反感,这充分说明了教育的失败。请记住费曼的话:「一个傻瓜能做到的事情,另一个傻瓜也能做到」。
规则
以下是关于高效间隔重复学习的规则。
规则按适用性进行排序(但不一定按重要性排序),通用性的规则排在前面,而最具体的规则排在后面。
由于许多例子涉及同时使用多条规则,所以我决定将例子与规则列表分开列出。
规则:先理解
不要试图记忆你不理解的内容。在将概念转化为记忆之前,你应该首先确保这些概念在你的头脑中是清晰的。这里的「清晰」可能因人而异,没有固定标准。我通常采用的方法是:深入挖掘、拓展并厘清文本内容,直到我感到对这一概念领域有了充分的把握,之后才开始制作抽认卡。
通常,在阅读一本书的同时你无法写下抽认卡,因为之后的信息可能会阐明或联系重要的概念。一个好方法是在阅读一章节时将临时抽认卡写在便签上,最后你可以整理和重组便签,直到你能够记忆这些内容。
规则:保持诚实
软件并不知道你是否正确地回忆了某些内容。你只对自己负责。如果你回忆错了,或者记得不太对,谨慎起见,请标记为「忘记」。
规则:保持学习乐趣
这对于保持学习习惯至关重要。如果复习抽认卡感觉像一项琐事,你会对此产生厌恶情绪。
我以前经常出现这个问题。我用了几种方法解决它:
- 拥有一个多元的知识库。保持正在学习的内容有多个主题,这样你不会因为长时间浏览相同主题而感到厌倦。通常,间隔重复软件会对卡片进行洗牌,如果你将所有牌组混合学习便可经常感到惊喜。
- 导致挫败感的常见原因是卡片太长,无法快速回忆,感觉像一项琐事。将大卡片拆分为小卡片,快速地翻过卡片会让你感觉很好。
- 难以回忆的卡片非常令人沮丧。我通过应用本文中描述的规则解决了这个问题。
规则:自我重复
记忆状况取决于重复次数和学习量。单张卡片要言简意赅,但整副卡组可以根据你的需要重复任意多次。
规则:按来源组织内容
按来源组织内容,而不是按主题。
原因是你经常会从多个来源获得信息:多本教科书,再加上维基百科,再加上讲义等等。每个来源可能有不同的知识组织方式。
不要浪费时间试图找到完美的组织方式。
为每个来源建立一个牌组。对于教科书,为每章节建立一个子牌组。对于数学教科书,可能在每个章节中再建立一个子子牌组,用于放置定理抽认卡。
这也让你更容易跟踪自己对一本教材的学习进度。
规则:编写原子化的抽认卡
抽认卡应该简短。它们应该涉及尽可能少的信息。它们应该像化学键一样,将独立的原子知识连接起来。
这是最重要的事情。把太多内容放在一张抽认卡上非常糟糕。
这个规则有两个原因:
- 冗长的卡片更难记忆。
- 客观评估自己的掌握程度比较困难:揭示答案时,你可能有些地方答对了,有些地方答错了。如果你点击「忘记」,就会过度复习已经掌握的部分。如果点击「记住」,又会对遗忘的内容复习不足。
这条规则有一个例外:如果你有一些小卡片,它们加起来包含了同样的信息,那么你也可以使用大卡片。你可以把大卡片看作是在测试你能否整合小卡片上的信息。
规则:双向提问
在可能的情况下,以两个方向来提问。
每当你遇到需要定义的术语时,最显而易见的做法就是根据术语来询问其定义。比如说:
问:群的阶是什么?
答:它的基。
但你也可以通过定义询问术语,例如:
问:群的基的术语是什么?
答:群的阶。
当遇到一些数学符号时,比如表示实数的 ,或者表示向量空间维数的
,你自然会想问这些符号是什么意思。
问:符号代表什么?
答:实数集。
你也可以反过来问问题:
问:表示实数集的符号是什么?
答:
规则:提问方式多样化
用多种方式提问。询问术语的正式定义和通俗解释。询问定理的严格表述和直观描述。正向反向都要提问。添加一些背景性的问题,比如「[某个概念]的直观理解是什么?」。还要提出一些能够将你知识图谱中不同概念联系起来的问题。
你的知识图谱之间的相互关联越多越好。
规则:缓存你的见解
在学习过程中,你常常能够通过思考刚刚阅读的内容,推导出一些教材中并未明确陈述的新知识。当你确认这些推论确实正确之后,将这些见解「缓存」会带来很大帮助——具体做法是为每个新发现的知识点制作一张复习卡片。这种方法不仅可以帮助你巩固所学,还能逐步构建起自己的知识体系。
规则:概念图谱
把你正在学习的概念视为一张图谱可能会有所帮助。在这张图谱中,每个节点代表一个具有特定属性的独立概念。而图谱中的边则是引导你从一个概念到另一个概念的问题。
规则:学习层次结构
许多知识都具有层次结构,比如「某个概念可以分为 A、B 或 C 几种类型」,或者反过来说,「A 是某个概念的一种」。这与面向对象编程中的概念类似:这些知识通过上下级关系相互联系。
关键是要从两个方向提问:自上而下「这个概念包含哪些子类?」和自下而上「这个具体类型属于哪个更大的概念?」。
这种思路与保持记忆卡片内容精炼的原则是一致的。即使某些信息本身并不是层次结构,将大型记忆卡片拆分成更小的卡片,实际上就是在构建一个卡片的层次体系。
规则:学习序列
为了高效记忆一个序列 ,你需要对
生成以下抽认卡:
| 问题 | 答案 |
|---|---|
| 第 $i$ 个元素是什么? | $A_i$ |
| $A_i$ 在序列中的位置? | $i$ |
| Ai 的下一个元素? | $A_{i+1}$ |
| $A_i$ 的前一个元素? | $A_{i-1}$ |
除此之外,你可能还需要:
- 一张测试卡片:考察你从头到尾背诵整个序列的能力。
- 一套完形序列卡片:将序列中的元素挖空,根据上下文填空,测试对整个序列的掌握情况。
你可以使用序列脚本自动生成上述抽认卡。
至于采用多全面的卡片组合,取决于所学习知识的性质。我个人在大多数情况下会使用完形卡片和测试卡片。
你可能会使用另一种类型的记忆卡片(我用这种方法来背诵诗歌)。这种卡片会提供一些上下文信息(序列中的前一个或两个项目),然后要求你填空。例如,如果你想学习序列(A,B,C,D),你可能会制作如下抽认卡:
| 问题 | 答案 |
|---|---|
| 开始,… | A |
| 开始,A,… | B |
| A,B,… | C |
| B,C,… | D |
有一个诗歌脚本可以帮你自动生成这些卡片。
示例
以下许多例子可能过于详尽:我们制作的抽认卡数量远超主题实际所需。但这是为了阐释一般规则。随着经验的积累,你会逐渐掌握某个特定主题需要多少问题,而且你的知识网络中不同部分之间的联系程度也会有所不同。
示例:岩浆的形成
以下内容摘自我的地质学笔记:
——————
岩浆是存在于地球表面以下的液态岩石。
形成岩浆的三个过程是:
- 温度升高:温度升高可以使岩石熔化。
- 压力降低:当压力降低时,原子能够更自由地移动,岩石就会转变为液态。
- 加入水分:水能降低岩石的熔点,因为水分子会破坏岩石的晶体键。
岩浆在三个地方形成:
- 热点: 地球深部的高温岩石在上升过程中,由于周围压力逐渐降低,最终熔化形成岩浆。
- 裂谷带: 当地壳板块分离时,下方密度较小的热岩石会上升填充裂隙。随着压力减小,这些岩石开始熔化。
- 俯冲带: 含水量丰富的海洋板块下沉至地幔。水分受热后上升,渗入上方的岩石中,引发岩石熔化。
——————
让我们系统地整理这些信息。我们需要记住三个要点:
- 岩浆的定义
- 岩浆的形成过程
- 岩浆的形成地点
首先是岩浆的定义:
| 问题 | 答案 |
|---|---|
| 岩浆是什么? | 地球表面以下的熔融岩石。 |
| 地球表面以下的熔融岩石叫什么? | 岩浆。 |
接下来,我们需要了解岩浆的形成过程。值得注意的是,我们应该将形成过程列表和其详细解释分开,以保持每个学习要点的简洁性。
因此,我们先列出岩浆的形成机制:
| 问题 | 答案 |
|---|---|
| 岩浆形成的主要过程有哪些? | 温度升高、压力降低以及水的加入。 |
接下来,我们需要对每个过程进行详细解释。关于温度升高导致岩石熔化这一点,我们无需多作解释:
| 问题 | 答案 |
|---|---|
| 为什么压力降低会导致岩石熔化? | 因为岩石中的原子获得了更大的运动自由度 |
| 为什么加入水会降低岩石的熔点? | 因为水分子会破坏岩石矿物中的化学键 |
第三:岩浆形成的地点。我们同样将地点列表与具体细节分开:
| 问题 | 回答 |
|---|---|
| 岩浆主要在哪些地方形成? | 地幔热点区域、地壳裂谷带和板块俯冲带。 |
然后我们深入探讨细节。对于每个岩浆形成的地点,我们需要了解其中涉及的具体过程,以及完整的因果关系。同时,我们还会反过来思考:哪些地质环境涉及了特定的岩浆形成过程。
| 问题 | 答案 |
|---|---|
| 热点区域的岩浆形成过程是什么? | 减压熔融。 |
| 裂谷带的岩浆形成过程是什么? | 减压熔融。 |
| 俯冲带的岩浆形成过程是什么? | 温度升高和水分增加。 |
| 哪些地质环境下会因压力释放而形成岩浆? | 热点和裂谷带。 |
| 哪些地质环境下会因温度升高和水分增加而形成岩浆? | 俯冲带。 |
| 热点地区的岩浆是如何形成的? | 当高温地幔物质上涌时,压力降低导致其发生熔融。 |
| 裂谷带的岩浆是如何形成的? | 当板块分离时,高温岩石上涌填充裂隙,压力降低导致其发生熔融。 |
| 俯冲带的岩浆是如何形成的? | 含水的地壳俯冲到地幔中,水转化为蒸汽并上升,水分的加入使上覆岩石发生熔融。 |
我们可以这样可视化所得到的知识图谱:
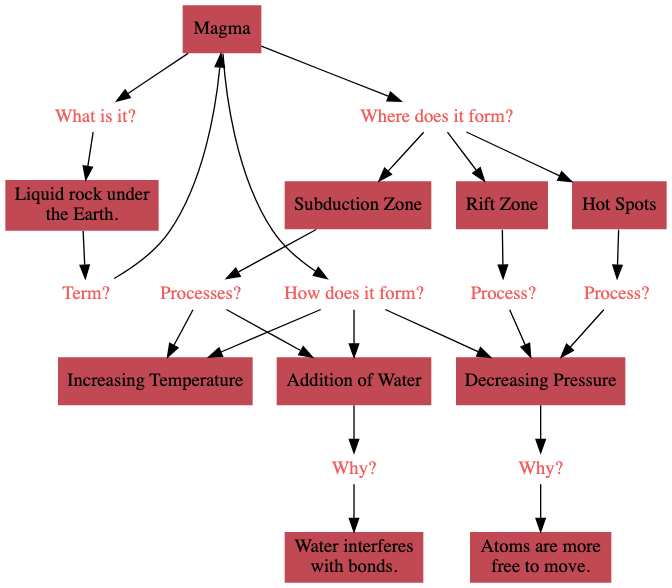
示例:板块构造理论
以下是关键信息:
——————
地球表面的地壳板块在相互接触的区域形成「板块边界」。板块边界可以分为三种类型:
- 汇聚型边界:两个板块相互靠近并发生碰撞。
- 离散型边界:两个板块相互分离,向相反方向移动。
- 转换型边界:两个板块沿着边界平行滑动。
——————
遵循抽认卡双向设计的原则,我们为「板块边界」这一概念制作两张抽认卡:
| 问题 | 答案 |
|---|---|
| 什么是板块边界? | 地壳板块相互接触的区域。 |
| 地壳板块相互接触的区域被称为什么? | 板块边界。 |
关于不同类型的板块边界,我们只需从概念到具体类型的方向提问(无需问「什么是转换型边界?」因为名称本身已经揭示了其性质):
| 问题 | 答案 |
|---|---|
| 板块边界有哪几种类型? | 汇聚型边界、离散型边界和转换型边界。 |
对于每种类型的板块边界,我们同样采用两种提问方式:
| 问题 | 答案 |
|---|---|
| 定义:汇聚型边界 | 构造板块相互靠近并碰撞的区域。 |
| 定义:离散型边界 | 构造板块相互远离的区域。 |
| 定义:转换型边界 | 构造板块沿着边界相对滑动的区域。 |
| 构造板块相互靠近的地质现象称为什么? | 汇聚型边界。 |
| 构造板块相互远离的地质现象称为什么? | 离散型边界。 |
| 构造板块相对滑动的地质现象称为什么? | 转换型边界。 |
图示展现了这些问题如何在知识图谱中连接各个概念:
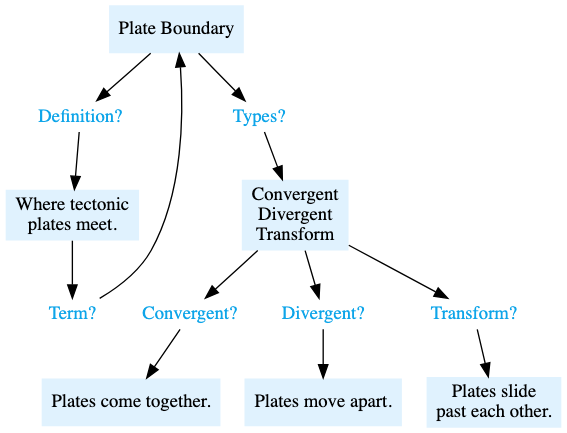
示例:神经细胞
——————
神经系统中的细胞主要分为两类:神经元和神经胶质细胞。神经胶质细胞可进一步分为大胶质细胞和小胶质细胞。其中,大胶质细胞又包括三种类型:星形胶质细胞、少突胶质细胞和施万细胞。
——————
这种结构可以通过以下图示直观地呈现:
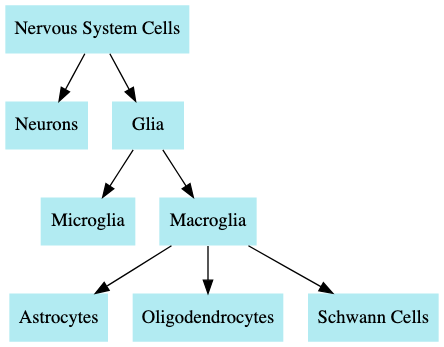
基于这种层级结构,我们可以设计一些由上至下的问题:
| 问题 | 答案 |
|---|---|
| 神经系统由哪些类型的细胞构成? | 神经元和胶质细胞。 |
| 胶质细胞可以分为哪些类型? | 小胶质细胞和大胶质细胞。 |
| 大胶质细胞包括哪些类型? | 星形胶质细胞、少突胶质细胞和施万细胞。 |
以下是一些自下而上的问题。当答案明显时,我们通常不会问这些问题。例如,「小胶质细胞/大胶质细胞属于什么类型」这个问题的答案是显而易见的。
| 问题 | 答案 |
|---|---|
| 星形胶质细胞属于哪一类? | 大胶质细胞。 |
| 少突胶质细胞属于哪一类? | 大胶质细胞。 |
| 施万细胞属于哪一类? | 大胶质细胞。 |
示例:神经元类型
这是一个简短的例子,说明如何保持卡片内容简洁,并使用层级结构来分解复杂信息。
以下是我的神经科学笔记摘录:
——————
神经元可以根据其功能分为三类:
- 感觉神经元:将感觉信息传入大脑。
- 运动神经元:向肌肉发送运动指令。
- 中间神经元:在中枢神经系统内部进行连接。这类神经元可进一步分为:
- 局部:与周围神经元形成局部回路。
- 中继:具有长轴突,负责在不同脑区之间传递信息。
——————
让我们先从一个错误的示范开始,即在一张卡片中塞入过多信息。
| 问题 | 答案 |
|---|---|
| 神经元的功能类别有哪些? | 感觉神经元:负责将感觉信息传入大脑。 运动神经元:负责向肌肉发送运动指令。 中间神经元:负责在中枢神经系统内部进行连接。 ( 太长了) |
| 中间神经元有哪些不同类型? | 局部:与附近的神经元形成神经回路。 中继:具有较长的轴突,负责不同脑区之间的信息传递。 ( 太长了) |
现在,让我们将术语与定义分开:
| 问题 | 答案 |
|---|---|
| 神经元可以分为哪几类主要功能类型? | 感觉、运动和中间。 |
| 感觉神经元的主要功能是什么? | 将外界环境的信息传入大脑的神经元。 |
| 运动神经元的主要作用是什么? | 将大脑的指令传递给肌肉的神经元。 |
| 中间神经元在神经系统中扮演什么角色? | 在中枢神经系统内部进行信息传递和处理的神经元。 |
| 中间神经元可以细分为哪两种类型? | 局部和中继。 |
| 局部中间神经元的主要特征是什么? | 与附近的神经元形成局部神经回路的中间神经元。 |
| 中继中间神经元的关键特点是什么? | 具有较长的轴突,能够在不同脑区之间传递信息的中间神经元。 |
现在我们进行反向提问:请根据给出的定义回答相应的神经科学术语。
| 问题 | 答案 |
|---|---|
| 将信息传入大脑的神经元称为什么? | 感觉神经元。 |
| 向肌肉发送指令的神经元称为什么? | 运动神经元。 |
| 在中枢神经系统内部相互连接的神经元称为什么? | 中间神经元。 |
| 与周围神经元形成局部回路的中间神经元称为什么? | 局部中间神经元。 |
| 在大脑不同区域之间传递信息的中间神经元称为什么? | 中继中间神经元。 |
示例:向量空间
以下是我们将要学习的内容:
——————
简单来说,向量空间是一个集合,其中的元素称为向量,这些向量可以进行加法运算和数乘运算。
更严格的数学定义是:在数域 上的向量空间是一个集合
,以及两种运算:
- 向量加法:
- 标量乘法:
这两种运算需要满足以下公理:
- 加法交换律
- 加法结合律
- 加法单位元
- 加法逆元
- 标量乘法单位元
- 分配律
——————
我们需要将其分解。让我们一步一步来。
首先,我们要区分非正式(直观)定义和正式定义:
| 问题 | 答案 |
|---|---|
| 简单来说,什么是向量空间? | 向量空间是一个数学概念,它描述了一个包含特定元素(称为向量)的集合。这些向量可以相互相加,也可以被数字(称为标量)放大或缩小。 |
| 从数学角度严格定义,什么是向量空间? | 在数学中,向量空间是指在某个数域 $\mathbb{F}$ 上定义的一个集合 $V$,其配备了两种基本运算:向量加法和标量乘法。 |
我们添加了一个关于符号的简短问题(你可以选择跳过这个问题,这是一个示例):
| 问题 | 答案 |
|---|---|
| 向量空间的元素叫什么? | 向量。 |
关于运算符号的问题:
| 问题 | 答案 |
|---|---|
| 向量加法运算的数学表示是什么? | $V \times V \to V$ |
| 标量乘法运算的数学表示是什么? | $V \times \mathbb{F} \to V$ |
关于公理的问题:
| 问题 | 答案 |
|---|---|
| 定义向量空间的基本公理有哪些? | 1. 加法交换律 2. 加法结合律 3. 加法单位元 4. 加法逆元 5. 标量乘法的单位元 6. 分配律 |
最后,让我们来询问每个公理的具体含义:
| 问题 | 答案 |
|---|---|
| 向量空间公理:加法交换律 | $u + v = v + u$ |
| 向量空间公理:加法结合律 | $u + (v + w) = (u + v) + w$ |
| 向量空间公理:加法零元 | $\exists 0 \in V : v + 0 = v$ |
| 向量空间公理:加法逆元 | $\forall v \in V, \exists -v \in V : v + (-v) = 0$ |
| 向量空间公理:标量乘法的单位元 | $1v = v$ |
| 向量空间公理:分配律 | $\forall v \in V, a,b \in \mathbb{F} : (a+b)v = av + bv$ |
下图可以帮助你直观地理解这些抽认卡及其之间的关系:
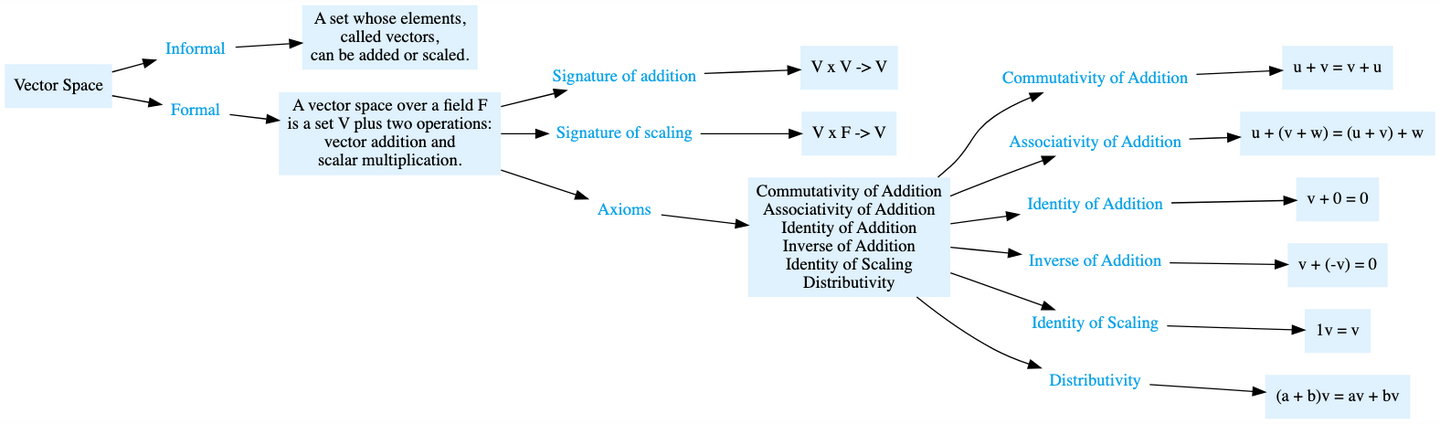
为了更全面地掌握这些概念,你还可以创建反向问题:
| 问题 | 答案 |
|---|---|
| 什么是允许其元素进行加法和数乘运算的集合? | 向量空间 |
| 请给出这个公理的名称:$u + v = v + u$ | 加法交换律 |
| 请给出这个公理的名称:$u + (v + w) = (u + v) + w$ | 加法结合律 |
| 请给出这个公理的名称:$\exists 0 \in V : v + 0 = v$ | 加法单位元 |
| 请给出这个公理的名称:$\forall v \in V, \exists -v \in V : v + (-v) = 0$ | 加法逆元 |
| 请给出这个公理的名称:1v=v | 标量乘法的单位元 |
| 请给出这个公理的名称:$\forall v \in V, a,b \in \mathbb{F} : (a+b)v = av + bv$ | 分配律 |
示例:奇偶群
——————
奇偶群是一个简单而富有洞察力的群论例子,它描述了偶数和奇数相加的规律。该群的基础集合为{偶,奇},其中「偶」表示所有偶数,「奇」表示所有奇数。群的运算表如下:
| + | 偶 | 奇 |
|---|---|---|
| 偶 | 偶 | 奇 |
| 奇 | 奇 | 偶 |
「偶」是单位元。这个群是阿贝尔群。
——————
我们可以创建相应的抽认卡:
| 问题 | 答案 |
|---|---|
| 什么是奇偶群? | 一个描述偶数和奇数加法规则的群。 |
| 奇偶群的阶是多少? | 2 |
| 奇偶群的基础集合是什么? | {偶,奇} |
| 奇偶群的单位元是什么? | 偶 |
| 奇偶群的运算是什么? | 基于偶数和奇数的加法规则 |
| 偶 + 偶 = | 偶 |
| 偶 + 奇 = | 奇 |
| 奇 + 偶 = | 奇 |
| 奇 + 奇 = | 偶 |
| 奇偶群是否为阿贝尔群?为什么? | 是的,因为满足加法交换律。 |
示例:逻辑后果
摘自我的逻辑学笔记:
——————
逻辑后果的两个概念是:
- 语义后果:如果在所有使
为真的解释中,
也必定为真,那么
是
的语义后果。这种关系用符号
表示。
- 句法后果:如果存在一个从
到
的证明,那么
是
的句法后果。这种关系用符号
表示。
简而言之,语义后果关注的是命题在各种可能解释下的真值关系,而句法后果则聚焦于命题之间的形式化推理过程。
——————
让我们从最基本的问题入手:
| 问题 | 答案 |
|---|---|
| 逻辑后果的两个核心概念是什么? | 语义后果和句法后果。 |
接下来,我们将深入探讨与语义后果相关的具体问题:
| 问题 | 答案 |
|---|---|
| 请定义语义后果。 | 如果在所有使 $P$ 为真的解释中,$Q$ 也必定为真,那么 $Q$ 是 $P$ 的语义后果。 |
| 用什么符号表示「$Q$ 是 $P$ 的语义后果」? | $P \models Q$ |
| $P \models Q$ 表达了什么意思? | $Q$ 是 $P$ 的语义后果 |
| 语义后果是通过什么来连接句子的? | 解释。 |
| 在逻辑后果的概念中,哪一种涉及到解释? | 语义后果。 |
然后是句法结果:
| 问题 | 答案 |
|---|---|
| 请定义句法后果 | 如果存在一个从 $P$ 到 $Q$ 的证明,那么 $Q$ 是 $P$ 的句法后果。 |
| 用什么符号表示「$Q$ 是 $P$ 的句法后果」? | $P \vdash Q$ |
| $P \vdash Q$ 表达了什么意思? | $Q$ 是 $P$ 的句法后果 |
| 句法后果是通过什么来连接句子的? | 证明。 |
| 在逻辑后果的概念中,哪一种涉及到证明? | 句法后果。 |
示例:时期划分
时间线是一个绝佳的例子,展示了如何通过层次化分解信息来帮助我们学习长序列。有时这种分解工作已经为我们事先完成了。
——————
地质年代表(GTS)将地球的地质历史记录划分为四个相互嵌套的时间单位:
- 宙是最大的时间单位,每个宙持续数亿年之久。
- 宙进一步细分为若干个代,每个代的持续时间从数千万年到数亿年不等。
- 代再往下划分为纪,每个纪的时间跨度从数百万年到数千万年不等。
- 最后,纪被细分为世,每个世持续数十万年到数百万年。
地球历史上的四个宙,按从最古老到最近的顺序排列如下:
- 冥古宙(从 45 亿年前到 40 亿年前)
- 太古宙(从 40 亿年前到 25 亿年前)
- 元古宙(从 25 亿年前到 5.38 亿年前)
- 显生宙(从 5.38 亿年前持续至今)
——————
我们需要了解以下三个方面:
- 地质年代表的定义。
- 地质年代表如何划分地球的历史。
- 地球历史中的四个宙。
让我们从最基本的概念入手,即地质年代表的定义:
| 问题 | 答案 |
|---|---|
| 地质年代表是什么? | 地球历史的时间线。 |
| 地球历史的时间线被称为什么? | 地质年代表。 |
地质时间单位按从大到小的顺序排列为:宙、代、纪、世。我们可以使用序列脚本来生成相关的学习卡片。以下是输入数据:
地质时间单位
宙
代
纪
世运行 cat units.txt | ./sequence.py > units.csv,然后将 units.csv 导入到Mochi,我们就能得到这些抽认卡:
| 问题 | 答案 |
|---|---|
| 地质时间单位: 请按从大到小的顺序列出所有单位 | 宙、代、纪、世。 |
| 地质时间单位: 最大的时间单位是什么? | 宙。 |
| 地质时间单位: 第二大的时间单位是什么? | 代。 |
| 地质时间单位: 第三大的时间单位是什么? | 纪。 |
| 地质时间单位: 最小的时间单位是什么? | 世。 |
| 地质时间单位: 宙在序列中排第几? | 1。 |
| 地质时间单位: 代在序列中排第几? | 2。 |
| 地质时间单位: 纪在序列中排第几? | 3。 |
| 地质时间单位: 世在序列中排第几? | 4。 |
| 地质时间单位: 宙的下一级单位是什么? | 代。 |
| 地质时间单位: 代的下一级单位是什么? | 纪。 |
| 地质时间单位: 纪的下一级单位是什么? | 世。 |
| 地质时间单位: 代的上一级单位是什么? | 宙。 |
| 地质时间单位: 纪的上一级单位是什么? | 代。 |
| 地质时间单位: 世的上一级单位是什么? | 纪。 |
其实你不需要全部都记。以下几张可能就足够了:
| 问题 | 答案 |
|---|---|
| 地质年代单位的层级是什么,从大到小排列? | 宙、代、纪、世。 |
| 地质年代中最大的时间单位是什么? | 宙。 |
| 地质年代中第二大的时间单位是什么? | 代。 |
| 地质年代中第三大的时间单位是什么? | 纪。 |
| 地质年代中最小的时间单位是什么? | 世。 |
既然这是一个概念层级结构,我们还需要了解每个单位的定义:
| 问题 | 答案 |
|---|---|
| 什么是宙? | 地质年代划分的一个单位。 |
| 什么是代? | 地质年代划分的一个单位。 |
| 什么是纪? | 地质年代划分的一个单位。 |
| 什么是世? | 地质年代划分的一个单位。 |
另外,由于每个单位都有其持续时间,我们还需要了解它们的时间跨度。这个问题可以从正反两个方向来提出:
| 问题 | 答案 |
|---|---|
| 一个宙的持续时间是多久? | 数亿年。 |
| 哪个地质年代单位持续数亿年? | 宙。 |
| 一个代的持续时间是多久? | 数千万至数亿年。 |
| 哪个地质年代单位持续数千万至数亿年? | 代。 |
| 一个纪的持续时间是多久? | 数百万至数千万年。 |
| 哪个地质年代单位持续数百万至数千万年? | 纪。 |
| 一个世的持续时间是多久? | 数十万至数百万年。 |
| 哪个地质年代单位持续数十万至数百万年? | 世。 |
接下来我们将讨论四个宙。这些宙构成了一个序列,我们不会再完整地走完整个流程,因为你可能已经再次使用了这些:
| 问题 | 答案 |
|---|---|
| 请按从最古老到最新的顺序列出地球历史的宙 | 冥古宙、太古宙、元古宙、显生宙 |
| 第一个宙是什么? | 冥古宙 |
| 第二个宙是什么? | 太古宙 |
| 第三个宙是什么? | 元古宙 |
| 第四个宙是什么? | 显生宙 |
我们也会问每个宙的开始和结束,前驱和后继:
| 问题 | 答案 |
|---|---|
| 冥古宙从何时开始? | 45 亿年前 |
| 冥古宙在何时结束? | 40 亿年前 |
| 哪个宙开始于 45 亿年前? | 冥古宙 |
| 哪个宙结束于 40 亿年前? | 冥古宙 |
| 太古宙的起始时间是? | 40 亿年前 |
| 太古宙的终止时间是? | 25 亿年前 |
| 40 亿年前开始的是哪个宙? | 太古宙 |
| 25 亿年前结束的是哪个宙? | 太古宙 |
| 元古宙从何时开始? | 25 亿年前 |
| 元古宙在何时结束? | 5.38 亿年前 |
| 25 亿年前开始的是哪个宙? | 元古宙 |
| 5.38 亿年前结束的是哪个宙? | 元古宙 |
| 显生宙的开始时间是? | 5.38 亿年前 |
| 显生宙何时结束? | 现在(仍在持续) |
| 5.38亿年前开始的是哪个宙? | 显生宙 |
| 目前仍在持续的宙是哪一个? | 显生宙 |
示例:有理数
让我们将这个概念提交到间隔重复中:
——————
有理数集合,用符号 表示,是所有可以表示为分数形式的数的集合,其中分子和分母都是整数,且分母不能为零。
用数学语言严格定义如下:
这里的 代表「商」(quotient)。
——————
在设计抽认卡时,我们可以通过概念图来直观地展示学习内容。首先,我们从核心概念——有理数开始:

接着,我们添加一个表示符号的节点,并通过两个相互关联的问题将其连接:

| 问题 | 答案 |
|---|---|
| 有理数集合的数学符号是什么? | $\mathbb{Q}$ |
| 数学符号 $\mathbb{Q}$ 表示什么? | 有理数集合 |
最后,我们可以加入有理数的严格定义和通俗解释:
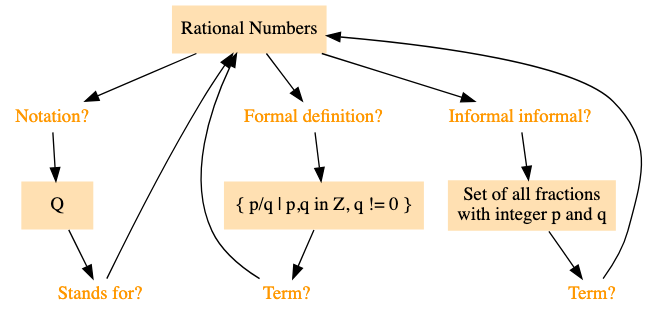
| 问题 | 答案 |
|---|---|
| 通俗地说,有理数集是什么? | 有理数集是由所有可以表示为分数形式的数组成的集合,其中分子和分母都是整数,且分母不为零。 |
| 数学上严格定义,有理数集是什么? | $$\mathbb{Q} = \left{\, \frac{p}{q} \,\, \middle |
| 整数之间的比值构成的集合在数学中称为什么? | 有理数集。 |
| 集合 $$\left\{\, \frac{p}{q} \,\, \middle| \,\, p, q \in \Z \land q \neq 0 \,\right\}$$ 在数学中表示什么? | 有理数集。 |
关于数学符号的补充说明:$\mathbb{Q}$ 在表示有理数集时的含义:
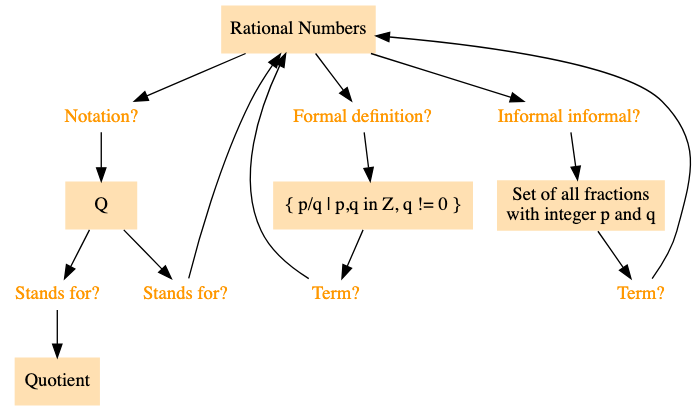
| 问题 | 答案 |
|---|---|
| 在数学中,为什么用 $\mathbb{Q}$ 来表示有理数集? | Q 代表英文单词「quotient」(商) |
示例:正则表达式
这个例子展示了如何通过两种方式提问。
以下问答卡片展示了从概念到具体正则表达式语法的对应关系:
| 问题 | 答案 |
|---|---|
| 在正则表达式中,用什么符号匹配一行文本的开头? | ^ |
| 在正则表达式中,用什么符号匹配一行文本的结尾? | $ |
| 在正则表达式中,用什么模式匹配任意单个数字? | \d |
除上述内容外,还可添加从正则表达式到概念的卡片:
| 问题 | 答案 |
|---|---|
| ^ 匹配什么? | 行的开始 |
| $ 匹配什么? | 行的结束 |
| \d 匹配什么? | 0 到 9 之间的任意数字 |
示例:电压
这是一个展示如何以不同方式提问的范例。
——————
和
两点之间的电压可以通过以下两种方式定义:
- 两点之间的电势差。
- 电荷量为
的粒子从
点移动到
点所做的功。
——————
这里的思路是:
- 首先,我们从电势差和功两个角度来询问电压的定义。
- 其次,我们还要询问每个定义所对应的专业术语。
据此,我们可以制作出以下抽认卡:
| 问题 | 答案 |
|---|---|
| 从电势的角度来看,电压是什么? | 两点之间的电势差。 |
| 从功的角度来看,电压是什么? | 单位电荷(1 库仑)从一点移动到另一点所做的功。 |
| 两点之间的电势差通常称为什么? | 电压。 |
| 单位电荷在两点之间移动所做的功通常称为什么? | 电压。 |
示例:同分异构体
——————
当两种化合物具有相同的化学式(即各元素的原子数相同),但三维结构不同时,我们称这两种化合物互为同分异构体。
异构体可以分为以下几类:
- 结构异构体:指分子式相同但原子连接方式不同的化合物。
- 立体异构体:指分子式和化学键相同,但空间排列不同的化合物。立体异构体可以进一步分为:
- 构象异构体:可以通过单键旋转相互转化的异构体。
- 构型异构体:不能通过单键旋转相互转化,必须打断化学键才能转化的异构体。构型异构体又可细分为:
- 对映异构体:互为不能重合的镜像的一对异构体。由于它们对平面偏振光的旋转方向不同,也被称为光学异构体。
- 非对映异构体:不是对映异构体的立体异构体。其中一个重要的类型是:
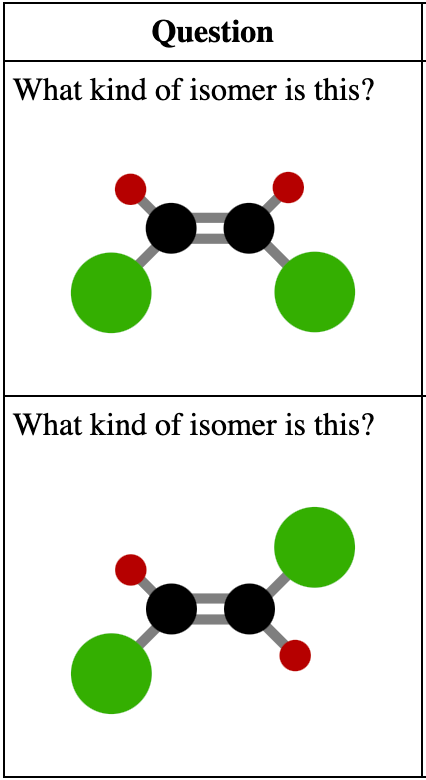
- 顺式/反式异构体:在具有刚性结构的分子中,当两个官能团可能处于同侧或异侧时形成的异构体。当两个官能团位于刚性结构的同一侧时,称为顺式异构体;当它们位于相对的两侧时,称为反式异构体。
下图展示了一个顺式异构体的例子:
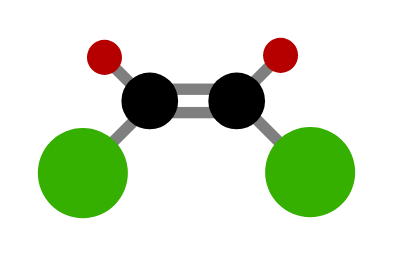
下图展示了一个反式异构体的例子:
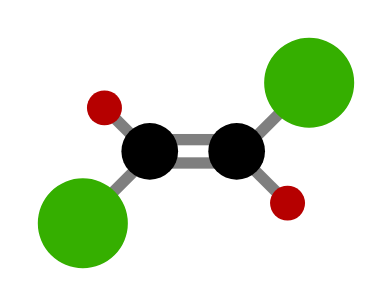
——————
这个概念体系相对简单明了:我们需要学习一个定义的层次结构。我们可以将学习任务分为两个部分:
- 首先,掌握定义。练习从术语到定义,以及从定义到术语的互相转换。
- 其次,理解层次结构:学习各种异构体的类型和亚类型之间的关系。
让我们从定义开始。首先我们按照正向顺序提出问题:
| 问题 | 答案 |
|---|---|
| 什么是异构体? | 当两种化合物具有相同分子式但三维结构不同,它们互为异构体。 |
| 什么是结构异构体? | 具有相同分子式,但原子之间的连接顺序或方式不同的化合物。 |
| 什么是立体异构体? | 分子式和化学键连接方式完全相同,但原子在三维空间中的排列不同的化合物。 |
| 什么是构象异构体? | 可以通过单键周围的自由旋转相互转化的异构体。 |
| 什么是构型异构体? | 必须打断化学键才能相互转化的异构体。 |
| 什么是对映异构体? | 互为镜像但不能重合。 |
| 什么是非对映异构体? | 属于立体异构体但不是对映异构体。 |
| 什么是顺反异构体? | 两个官能团可以位于刚性结构同侧(顺式)或异侧(反式)的异构体。 |
然后是反向定义:
| 问题 | 答案 |
|---|---|
| 分子式相同但三维结构不同的化合物,称为什么? | 异构体 |
| 分子式相同但化学键连接方式不同的异构体,称为什么? | 结构异构体 |
| 化学键连接相同但空间排列不同的异构体,称为什么? | 立体异构体 |
| 可通过单键自由旋转相互转化的异构体,称为什么? | 构象异构体 |
| 需要断键才能相互转化的异构体,称为什么? | 构型异构体 |
| 与镜像不能重合的异构体,称为什么? | 对映异构体 |
| 属于立体异构体但不是对映异构体,称为什么? | 非对映异构体 |
| 官能团位于刚性结构同侧或异侧的异构体,称为什么? | 顺式/反式异构体 |
为了保持每个知识点的独立性,我们省略了一些信息。现在需要提出问题来回忆那些被省略的信息:
| 问题 | 答案 |
|---|---|
| 对映异构体的另一个专业术语是什么? | 光学异构体。 |
| 为什么对映异构体也被称为光学异构体? | 这是由于它们能够旋转平面偏振光的特性。 |
| 光学异构体是指什么? | 这是对映异构体的另一种专业表述。 |
| 什么是顺式异构体? | 两个官能团位于刚性结构同一侧的异构体。 |
| 当一个异构体的两个官能团位于刚性结构的同一侧时,称为什么? | 顺式异构体。 |
| 什么是反式异构体? | 两个官能团位于刚性结构相对两侧的异构体。 |
| 当一个异构体的两个官能团位于刚性结构的相对两侧时,称为什么? | 反式异构体。 |
现在,我们来探讨这些概念在化学分类体系中的层级关系。我们首先从概念的层级结构出发,从上层概念到下层概念进行提问:
| 问题 | 答案 |
|---|---|
| 异构体可以分为哪两大类? | 结构异构体和立体异构体。 |
| 立体异构体又可以细分为哪两类? | 构象异构体和构型异构体。 |
| 构型异构体包括哪两种? | 对映异构体和非对映异构体。 |
| 非对映异构体中最常见的是哪种? | 顺式/反式异构体。 |
然后从下层到上层:
| 问题 | 答案 |
|---|---|
| 结构异构体属于? | 异构体 |
| 立体异构体属于? | 异构体 |
| 构象异构体属于? | 立体异构体 |
| 构型异构体属于? | 立体异构体 |
| 对映异构体属于? | 构型异构体 |
| 非对映异构体属于? | 构型异构体 |
| 顺式/反式异构体属于? | 非对映异构体 |
最后,举几个例子:
| 问题 | 答案 |
|---|---|
| 下图所示的是哪种异构体? | 顺式异构体 |
| 下图所示的是哪种异构体? | 反式异构体 |
示例:十二生肖
假设你想记住:
——————
- 鼠
- 牛
- 虎
- 兔
- 龙
- 蛇
- 马
- 羊
- 猴
- 鸡
- 狗
- 猪
——————
索引到元素的抽认卡:
| 问题 | 答案 |
|---|---|
| 第 1 个生肖是什么? | 鼠 |
| 第 2 个生肖是什么? | 牛 |
| 第 3 个生肖是什么? | 虎 |
| 第 4 个生肖是什么? | 兔 |
| 第 5 个生肖是什么? | 龙 |
| 第 6 个生肖是什么? | 蛇 |
| 第 7 个生肖是什么? | 马 |
| 第 8 个生肖是什么? | 羊 |
| 第 9 个生肖是什么? | 猴 |
| 第 10 个生肖是什么? | 鸡 |
| 第 11 个生肖是什么? | 狗 |
| 第 12 个生肖是什么? | 猪 |
元素到索引的抽认卡:
| 问题 | 答案 |
|---|---|
| 鼠是第几个生肖? | 1 |
| 牛是第几个生肖? | 2 |
| 虎是第几个生肖? | 3 |
| 兔是第几个生肖? | 4 |
| 龙是第几个生肖? | 5 |
| 蛇是第几个生肖? | 6 |
| 马是第几个生肖? | 7 |
| 羊是第几个生肖? | 8 |
| 猴是第几个生肖? | 9 |
| 鸡是第几个生肖? | 10 |
| 狗是第几个生肖? | 11 |
| 猪是第几个生肖? | 12 |
后继抽认卡:
| 问题 | 答案 |
|---|---|
| 鼠后面是什么? | 牛 |
| 牛后面是什么? | 虎 |
| 虎后面是什么? | 兔 |
| 兔后面是什么? | 龙 |
| 龙后面是什么? | 蛇 |
| 蛇后面是什么? | 马 |
| 马后面是什么? | 羊 |
| 羊后面是什么? | 猴 |
| 猴后面是什么? | 鸡 |
| 鸡后面是什么? | 狗 |
| 狗后面是什么? | 猪 |
前驱抽认卡:
| 问题 | 答案 |
|---|---|
| 牛前面是什么? | 鼠 |
| 虎前面是什么? | 牛 |
| 兔前面是什么? | 虎 |
| 龙前面是什么? | 兔 |
| 蛇前面是什么? | 龙 |
| 马前面是什么? | 蛇 |
| 羊前面是什么? | 马 |
| 猴前面是什么? | 羊 |
| 鸡前面是什么? | 猴 |
| 狗前面是什么? | 鸡 |
| 猪前面是什么? | 狗 |
示例:2 的幂
让我们来记忆 2 的前 16 个幂:
——————
——————
正面卡片(求幂的结果):
| 问题 | 答案 |
|---|---|
| $2^{2}$ | 4 |
| $2^{3}$ | 8 |
| $2^{4}$ | 16 |
| $2^{5}$ | 32 |
| $2^{6}$ | 64 |
| $2^{7}$ | 128 |
| $2^{8}$ | 256 |
| $2^{9}$ | 512 |
| $2^{10}$ | 1024 |
| $2^{11}$ | 2048 |
| $2^{12}$ | 4096 |
| $2^{13}$ | 8192 |
| $2^{14}$ | 16384 |
| $2^{15}$ | 32768 |
| $2^{16}$ | 65536 |
反面卡片(根据结果求指数):
| 问题 | 答案 |
|---|---|
| $\log_2 4$ | 2 |
| $\log_2 8$ | 3 |
| $\log_2 16$ | 4 |
| $\log_2 32$ | 5 |
| $\log_2 64$ | 6 |
| $\log_2 128$ | 7 |
| $\log_2 256$ | 8 |
| $\log_2 512$ | 9 |
| $\log_2 1024$ | 10 |
| $\log_2 2048$ | 11 |
| $\log_2 4096$ | 12 |
| $\log_2 8192$ | 13 |
| $\log_2 16384$ | 14 |
| $\log_2 32768$ | 15 |
| $\log_2 65536$ | 16 |
最后,我有一张测试卡,要求我按顺序回忆整个序列。
示例:Rilke 的诗
让我们记住这首诗:
——————
Archaic Torso of Apollo
Rainer Maria Rilke
We cannot know his legendary head
with eyes like ripening fruit. And yet his torso
is still suffused with brilliance from inside,
like a lamp, in which his gaze, now turned to low,
gleams in all its power. Otherwise
the curved breast could not dazzle you so, nor could
a smile run through the placid hips and thighs
to that dark center where procreation flared.
Otherwise this stone would seem defaced
beneath the translucent cascade of the shoulders
and would not glisten like a wild beast’s fur:
would not, from all the borders of itself,
burst like a star: for here there is no place
that does not see you. You must change your life.
——————
你可以使用序列脚本来执行这个过程,但那可能显得有些生硬和机械。不如我们采用诗歌脚本,它会向我们展示两行上下文,然后要求我们补全下一行。生成的抽认卡如下所示:
| 问题 | 答案 |
|---|---|
| 开头 ... | We cannot know his legendary head |
| 开头 We cannot know his legendary head ... | with eyes like ripening fruit. And yet his torso |
| We cannot know his legendary head with eyes like ripening fruit. And yet his torso ... | is still suffused with brilliance from inside, |
| with eyes like ripening fruit. And yet his torso is still suffused with brilliance from inside, ... | like a lamp, in which his gaze, now turned to low, |
| is still suffused with brilliance from inside, like a lamp, in which his gaze, now turned to low, ... | gleams in all its power. Otherwise |
依此类推。你应该已经领会了其中的规律。
示例:药理学
——————
药物的解离常数( )是指在实验中,当一半的结合位点被药物分子占据时所对应的药物浓度。
——————
这个例子展示了如何缓存你的见解。从这段描述中,我们可以进一步推导出:
- 当
值较高时,表明药物对结合位点的亲和力低,这是因为需要更高的药物浓度才能达到相同的结合程度。
- 相反,当
值较低时,意味着药物对结合位点的亲和力高,因为只需较低的浓度就能实现相同的占有率。
根据上述两点,我们还可以得出一个重要结论:
与结合亲和力成反比关系。
基于这些信息,我们可以提出一系列问题:
| 问题 | 答案 |
|---|---|
| 药物占据一半结合位点时的浓度,其专业术语是什么? | 解离常数。 |
| 解离常数通常用什么符号表示? | $K_d$ |
| $K_d$ 代表什么? | 解离常数。 |
| $K_d$ 值较低意味着什么? | 药物具有高结合亲和力。 |
| 为什么 $K_d$ 值低能反映出高结合亲和力? | 因为较少的药物分子就能达到相同的占有率。 |
| $K_d$ 值较高代表什么? | 药物具有低结合亲和力。 |
| 为什么 $K_d$ 值高表明结合亲和力低? | 因为需要更多的药物分子才能达到相同的占有率。 |
| 如果已知药物的结合亲和力高,这说明其 $K_d$ 值如何? | $K_d$ 值较低。 |
| 反之,若药物的结合亲和力低,其 $K_d$ 值会如何? | $K_d$ 值较高。 |
| 请描述 $K_d$ 与结合亲和力之间的关系。 | $K_d$ 与结合亲和力成反比。 |
| $K_d$ 与结合亲和力成比例关系。 | 反。 |
图示说明:
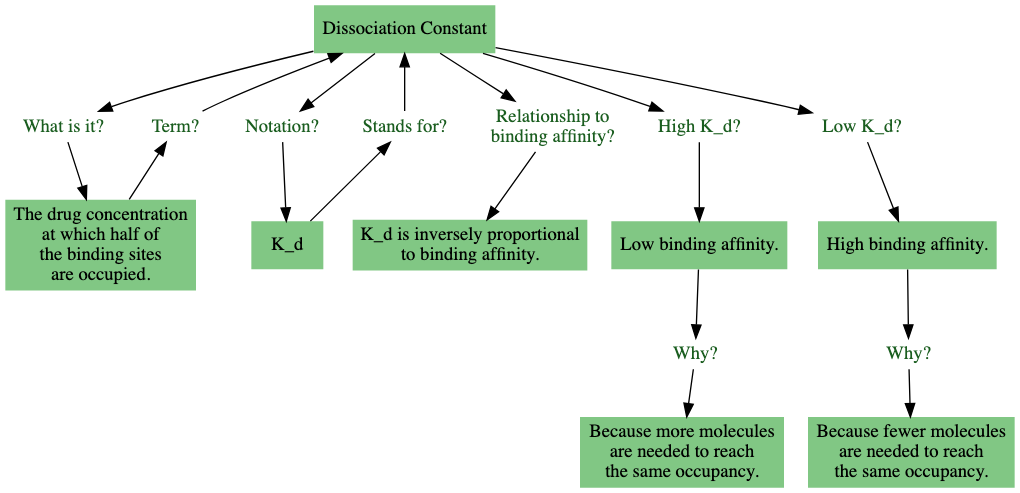
示例:杂项
案例 1:
美国国债(US Treasury bonds)通常被称为「国库券」(treasuries)。
你可以制作如下的正反面复习卡:
| 正面(问题) | 反面(答案) |
|---|---|
| 美国国债的常用简称是什么? | 国库券 |
| 「国库券」指的是哪种金融产品? | 美国国债 |
案例2:
的导数是
。
你可以围绕导数和积分创建以下复习卡:
| 正面(问题) | 反面(答案) |
|---|---|
| $\sin x$ 的导数是? | $\cos x$ |
| $\cos x$ 的积分是? | $\sin x$ |
脚本
如果纯靠人工制作所有抽认卡,许多规则将难以落实,因为这个过程会异常繁琐。幸运的是,我们可以借助自动化工具来简化这一过程。
我已将我使用的脚本上传至这个代码仓库。这些脚本主要参考了 Gwern 的脚本。
序列脚本
这个脚本可以根据学习序列规则中的原则,自动生成用于学习序列的闪卡。
假设我们有一个名为 greek.txt 的输入文件,内容如下:
希腊字母表
Alpha
Beta
Gamma我们可以运行 cat greek.txt | ./sequence.py > cards.csv 来生成以下抽认卡:
| 问题 | 答案 |
|---|---|
| 希腊字母表: 请列出序列中的全部元素 | Alpha、Beta、Gamma |
| 希腊字母表: 序列的第一个元素是? | Alpha |
| 希腊字母表: 序列的第二个元素是? | Beta |
| 希腊字母表: 序列的第三个元素是? | Gamma |
| 希腊字母表: Alpha 在序列中的位置是? | 1 |
| 希腊字母表: Beta 在序列中的位置是? | 2 |
| 希腊字母表: Gamma 在序列中的位置是? | 3 |
| 希腊字母表: Alpha 之后是哪个字母? | Beta |
| 希腊字母表: Beta 之后是哪个字母? | Gamma |
| 希腊字母表: Beta 之前是哪个字母? | Alpha |
| 希腊字母表: Gamma 之前是哪个字母? | Beta |
以及完形填空卡:
| 完形填空 |
|---|
| 希腊字母表: 序列中的元素依次为:[[Alpha]]、[[Beta]]、[[Gamma]] |
诗歌脚本
poetry.py 脚本生成一种特殊的抽认卡。在这种抽认卡中,你会看到一首诗的两行,然后需要回忆出下一行。想了解如何使用这个脚本,可以参考这个链接。
软件
Anki 是大多数人的首选记忆卡片软件。作为一款开源软件,它拥有丰富的插件资源和免费的卡片同步服务,自然而然成为了用户的默认选择。
我个人则更倾向于使用 Mochi。相比 Anki,Mochi 拥有更加精美的用户界面,这让使用过程更加愉悦,有助于养成良好的学习习惯。此外,Mochi 原生支持图片完形填空功能,无需依赖额外插件即可使用。
Anki 唯一让我青睐的而 Mochi 所缺失的功能是笔记类型。Anki 的笔记类型允许你从同一组结构化信息生成多张卡片。举个例子,你可以创建一个「化学元素」笔记类型,包含「名称」、「符号」、「原子序数」等字段,以及如下卡片模板:
| 问题 | 答案 |
|---|---|
| {name} 的符号是什么? | {symbol} |
| {name} 的原子序数是多少? | {z} |
| 符号 {symbol} 代表那个元素? | {name} |
| 什么元素的原子序数是 {z}? | {name} |
因此,从一条笔记(“铪”、“Hf”、“72”)中,你可以自动衍生出四张抽认卡。如果你编辑了笔记内容,所有相关的卡片都会自动更新。Mochi 软件缺乏这个功能,不过实际使用起来也不算太糟。你可以通过填空删除法来实现类似的效果。
现有技术
在学习闪卡制作领域,最具影响力的参考资料当属 1999 年发表的一篇经典论文。这篇文章出自 SuperMemo 软件创始人 Piotr Woźniak 之手,题为《高效学习:构建知识的二十条准则》[2]。我对文中的大部分观点都深表认同。现在,让我重点阐述其中几个核心原则:
- 理解先于记忆:在开始记忆之前,务必确保你对概念有透彻的理解。「透彻理解」这个标准可能因人而异,我的方法是深入探究、拓展和厘清概念,直到我能够自如地阐述这些知识为止。
- 卡片应该是原子化的:每张卡片只对应一个最基本的概念单元。
- 避免记忆冗长的序列。
- 避免记忆大量无序的信息。
- 使用简洁明了的语言表述。
- 适度的重复是有益的:不要害怕重复表达!
结语
希望这些规则和示例能对你的学习有所裨益。现在,拿起一本教科书,开始学习一些实用的知识吧。
Thoughts Memo 汉化组译制
感谢主要译者 changxvv、claude-3.5-sonnet,校对 Jarrett Ye、Suntiania
原文:Effective Spaced Repetition (borretti.me)
参考
1. 高效学习的间隔重复 ./420105707.html2. Anki高考的20条原则—来自《有效的学习:组织知识的20条原则》 https://www.kancloud.cn/ankigaokao/incremental_learning/2454060
专栏:AnkiX高考
围绕「Anki」和高考备考,面向广大高中生,交流作者们对「Anki」和高考的认识与见解,分享同学们整理的高中知识牌组,带每个考生高效学习!

