第十九章 交错练习（混合练习）

⠀⠀⠀摘要：交错练习（或混合练习）指的是同时推进多种技能，每种技能完成少量练习。与此相对的是分块练习，集中高强度练习一个技能。分块练习可能会让人误以为自己已经熟练掌握，因为它使学生头脑僵化，机械地将一种解决方案应用于一种问题。相反，交错练习是一种更有效的练习策略，因为交错练习创造了一种「合意困难」，极大地促进了知识的记忆和泛化。尽管交错练习的有效性已有证明，但在课堂上采用仍面临阻力，因为人们倾向于简单且收效明显的练习，哪怕这些提升转瞬即逝，且无法转化为考试成绩。

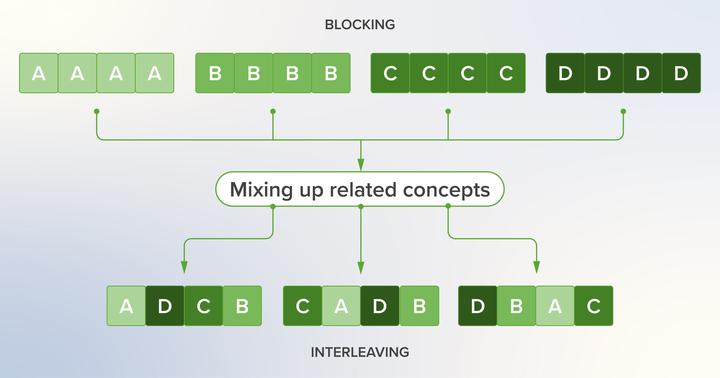
交错练习与分块练习

在传统课堂中，家庭作业通常属于同一主题。例如，如果学生在课堂上学习了多位数减法，老师可能布置15 道题当做家庭作业，来练习这一技能。这种方法被称为分块练习，即连续多次练习同一种技能。

虽然在初学一项技能时，分块练习是有益的，但对于复习来说，它对长期记忆的建立非常低效。与其让 10 道复习题集中在一次作业中，不如将它们分散到多个作业中，每个作业涵盖多种已学主题，这样效果更好。

例如，其中一个作业可能包含以下题目分布：

• （3 道题）多位数减法
• （3 道题）一位小数加法
• （3 道题）将一位小数转换为分数
• （3 道题）将假分数转换为带分数
• （3 道题）用多位数加法解决应用题

这种策略被称为交错练习（也称为多样化练习或混合练习）。

交错练习的好处

| 效率

交错练习的一个优势在于，一次交错练习中，多个不同的主题都能得到最小有效剂量的复习，而分块练习则仅集中于一个主题，导致大部分复习的收益递减，白白浪费。正如 Rohrer & Pashler (2007) 在《在不增加学习时间的情况下提高记忆》一文中所述：

⠀⠀⠀「我们的研究结果表明，一次专注于某些材料的学习会话应持续足够长的时间以确保掌握，但对同一材料的立即进一步学习是时间的低效利用。……当学生达到无误表现后继续学习被称为过度学习。……虽然过度学习通常会在短期内提高表现，但其益处会随着时间的推移急剧减少。

⠀⠀⠀……

⠀⠀⠀由于过度学习比不过度学习需要更多的学习时间，关键问题在于过度学习的好处与将相同时间用于其他用途的好处相比如何。……将这段学习时间用于复习几周、几个月甚至几年前学习的材料，通常会比继续学习刚刚学到的材料带来更大的收益。

⠀⠀⠀本质上，过度学习提供的回报非常有限，因为随着每增加一个单位的不间断学习时间，学习时间的投资回报会越来越小。」

如在其他地方的引用：

⠀⠀⠀「……过度学习具有集中练习的缺陷，当可以选择时，我们的研究结果表明，过度学习通常是学习时间的低效利用。」——Pashler et al. (2007)

⠀⠀⠀「……典型的数学作业包含许多围绕同一技能或概念的问题，但证据显示，学生在连续做多个同类问题时几乎没有获得长期益处（例如，Lyle、Bego、Hopkins、Hieb 和 Ralston，2020）。」——Rohrer & Hartwig (2020)

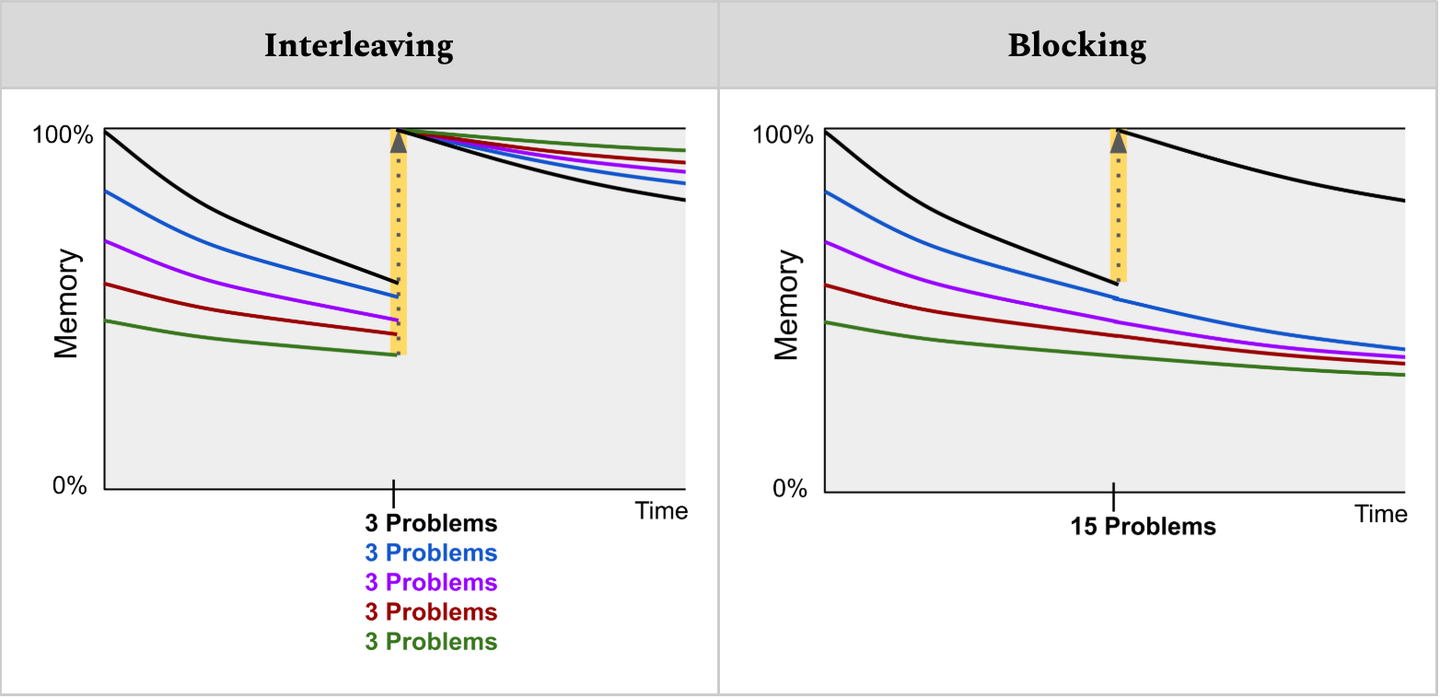
这可以通过遗忘曲线来直观表现（如下所示），并且它提供了一种有效的方法，Math Academy 用于选择交错复习的主题：简单地选择那些间隔重复即将到期（或最接近到期）的主题。

| 辨别学习和类别归纳学习

交错练习的另一个好处是，它不仅帮助学生练习解决问题的技巧，还增强了真正掌握知识所需的其他一些技能（参见 Rohrer, 2012 的综述）：

• （辨别学习）将问题与合适的解决方案匹配——例如，方程 x² + 3x + 2 = 0 和 x + 3x + 2 = 0 看起来相似，但解决方法截然不同。
  
  
• （类别归纳学习）识别一些通用特征，来区分不同问题，分别运用不同解题方法

正如 Taylor & Rohrer (2010) 所述：

⠀⠀⠀「然而，当练习题目被分块时，学生能够成功解决一组练习题，而无需学习如何将问题与技能配对。实际上，因为所有题目都与主题相关——通常是紧接在前一课中讲授的主题——学生可以在阅读题目之前为每个练习题选择合适的方法。虽然这降低了练习题的难度，但学生实际上依赖于一种辅助。不幸的是，当这些同类问题出现在综合考试、标准化测试或后续研究生涯中时，这一弱点就显露出来了。

⠀⠀⠀相比之下，交错练习让学生有机会练习将每种问题与合适的方法配对的能力。不仅限于统计课程，将问题与合适的方法或概念配对的应用在数学中普遍存在。

⠀⠀⠀例如，应用题之所以难以解决，一部分原因在于题目很少会明确指出需要使用哪种方法或概念。例如，有道题目是「如果一只虫子向东爬行 8 米，然后向北爬行 15 米，它离起点有多远？」，解题要求学生推断需要使用勾股定理。然而，如果这道题出现在一组明确要求使用勾股定理的问题之后，这种推断就不再需要（例如，如果直角三角形的两条边长分别为 8 和 15 米，那么它的斜边长度是多少？）。因此，分块练习可能大大降低应用题的教学价值。

⠀⠀⠀再举一个例子，值得注意的是，分块练习可能会导致学生无法区分不同类型的问题，即使这些问题在表面上并不相似。例如，在小学中，学生通常被教导如何找到两个整数的最大公因数和最小公倍数。因此，这两种问题的指令很容易区分（「找出最大公因数……」与「找出最小公倍数……」）。然而，如果每种类型的练习题都被分块，学生可能会忽略指令，而只关注问题中变化的信息（即一对整数）。学生可能仅仅通过重复相同的步骤来解决问题，而不去思考为什么这样做是合适的。」

| 实验支持

交错练习的好处得到了众多研究的支持，这些研究涵盖了广泛的领域，包括数学、其他学术科目、认知任务、运动技能，甚至体育练习（参见 Rohrer, 2012 的综述）。正如 Rohrer (2009) 总结的那样：

⠀⠀⠀「实验表明，通过引入间隔练习或混合练习，测试成绩可以显著提高，这两者是混合复习的两个核心特征。此外，间隔和混合都不需要增加练习题的数量，这意味着这两个特征提高了效率和效果。……它对数学学习的影响值得教师和研究人员给予更多关注。」

虽然分块练习可以更快地提高表现（这使其在初学技能时很有用），但交错练习极大地促进了记忆和泛化（这使其成为更有效的复习策略）。正如 Rohrer, Dedrick, & Stershic (2015) 所阐述的那样：

⠀⠀⠀「……相同类型的问题有一小部分可能就好了，特别是学生刚接触某类问题后刚开始做作业的时候，因为它给了学生专注于执行策略（例如，程序步骤和计算）的机会。然而，随着学生连续完成多个同类问题，他们的额外努力的收益可能会迅速递减（例如，Rohrer & Taylor, 2006; Son & Sethi, 2006）。」

交错练习的益处再怎么讲也不为过。尤其是数学学习。Taylor & Rohrer (2010) 发现，仅仅是将练习题目进行交错而不是分块，测试成绩就能翻倍。Rohrer, Dedrick, & Stershic (2015) 在研究不同年龄段的学生和更复杂的数学问题时，再次验证了这一现象。正如《科学美国人》（Pan, 2015）总结的那样：

⠀⠀⠀「这项为期三个月的研究中，教师教授七年级学生斜率和图形问题。每周的课程基本与标准教学无异，但家庭作业的设计采用了交错或分块的形式。交错设计中，不同类型的旧题和新题混合在一起。在九个参与班级中，五个班级对斜率问题使用交错设计，对图形问题使用分块设计；其余四个班级则相反。

⠀⠀⠀在最后一节课的五天后，每个班级为所有学生举行了一次复习课。一次突击期末测试在一天或一个月后进行。结果如何？当测试在一天后进行时，交错练习的问题得分提高了 25%；在一个月后，交错练习的优势增加到了 76%。」

正如 Rohrer, Dedrick, & Stershic (2015) 进一步解释的，进行交错练习的学生在延迟期间对测试材料的记忆保持明显优于分块练习的学生：

⠀⠀⠀「……交错练习不仅优于分块练习，它几乎使学生对遗忘的免疫，因为即使测试延迟时间增加 30 倍，测试分数也仅下降不到十分之一（从 80% 降至 74%）。

⠀⠀⠀……

⠀⠀⠀在此和其他研究中观察到交错练习产生显著效果的另一个原因是，交错的数学练习本质上确保了学生分散他们的练习。也就是说，除了在作业中并列不同类型的问题外，同类问题在不同的作业中也被分散安排。」

合意困难：为什么交错练习未被充分利用

那么，为什么交错练习很少应用到课堂上呢呢？还是那个道理。交错练习不仅偏离传统教学模式，更有研究表明，人们对其也有和主动学习类似的误解：交错练习提高学生认知参与度，从而取得更好的学习效果，但学生往往错误地以为，这种额外的认知劳动是学习效果不佳的表现，而实际上情况正好相反（Kornell & Bjork, 2008）。请看以下具体例子（Brown, Roediger, & McDaniel, 2014, pp.65）：

⠀⠀⠀「在交错练习中，你不会完成一个主题的所有练习后再转到另一个主题，而是在每套练习完成之前就切换。我们的一位朋友描述了他的经历：

⠀⠀⠀『我去上冰球课，学习滑冰技巧、控球和射门。我注意到我很沮丧，因为每当我们练习一点滑冰，我我觉得自己掌握了时，我们就转到控杆。我回家时就会很沮丧，心想，为什么教练不让我们继续练习直到我们掌握呢？』

⠀⠀⠀这种教练其实很少见，他懂得交错技能比每次专注一项能力的效果好。运动员感到沮丧是因为学习进展不快，但相比每次训练都专注于一项技能，下周他在所有方面都会表现得更好，比如滑冰、控球等。」

相比之下，分块练习创造了一种更舒适的流畅学习感，通过减少认知参与来人为地提高练习表现。当连续多次练习一种技能时，学生会陷入机械化的节奏中，机械地将一种解决方案应用于一种问题。这种机械性是非常明显的：在一项测量练习过程中「走神」的研究中，发现人们在分块练习时比在交错练习时更容易走神（Metcalfe & Xu, 2016）。但这种人为提高的练习表现会误导学生认为他们学得更好，尽管这种效果很快消失，并且实际上并没有转化为测试表现。

正如 Rohrer (2009) 总结的那样：

⠀⠀⠀「一种在降低练习表现的同时提高测试表现的特征被 Bjork 和他的同事描述为一种合意困难，间隔和混合是其中两个最显著的特征。正如这些研究人员所指出的，学生和教师有时会避免合意困难，如间隔和混合，因为他们错误地认为导致较差练习表现的特征也会导致较差的学习。」

在学术文献中，一种使任务更具挑战性、减缓学习进度但能提高记忆和迁移能力的练习条件，被称为合意困难。正如 Rohrer & Hartwig (2020) 所详细说明的：

⠀⠀⠀「间隔和交错都是合意困难现象的例子（Bjork, 1994），这是本论坛关注的焦点。合意困难是一种学习方法，与其他方法相比，它使练习变得更具挑战性，但能提高后续测试的成绩（例如，Bjork & Bjork, 2014; Bjork, 2018; Bjork & Bjork, 2019; Bjork & Kroll, 2015; Schmidt & Bjork, 1992）。」

许多认知学习策略引入了合意困难——例如，Bjork & Bjork（2011）列举了一些：

⠀⠀⠀「这些合意困难（Bjork, 1994; 2013）包括改变学习条件，而不是保持它们的恒定和可预测；交错不同主题的教学，而不是按主题分组教学（称为分块）；在给定主题上分散学习，而不是集中学习；以及使用测试而不是演示作为学习活动。」

然而，正如 Rohrer & Hartwig (2020) 解释的那样，合意困难的概念可能不太符合直觉：

⠀⠀⠀「困难可能是合意的，这并不符合直觉。事实上，许多人错误地认为在练习中达到的流畅程度是评估策略长期效果的可靠指标（Bjork, Dunlosky, & Kornell, 2013）。确实，许多困难是不理想的，因为它们不仅妨碍练习表现，还妨碍测试成绩，比如学生在看电视时做作业。」

此外，正如 Robert Bjork（1994）所解释的，典型的教师往往被激励去最大化学生的即时表现和/或幸福感，这使得他们不愿意引入合意困难：

⠀⠀⠀「对相关研究文献的最新综述（例如，Christina & Bjork, 1991; Farr, 1987; Reder & Klatzky, 1993; Schmidt & Bjork, 1992）毫无疑问地表明，许多最有效的训练方法——就训练后的记忆保持和迁移能力而言——都有一个共同的特点，即它们给学习者带来了困难。

⠀⠀⠀……

⠀⠀⠀如果研究结果如此明确，为什么……效率低下的方法仍然在现实世界训练计划中如此常见？……[典型的培训师往往过于关注学员的日常表现和反馈反应。实际上，培训师容易受到一种操作性条件反射的影响，其中的强化事件是学员在即时表现和/或幸福感上的改善。

⠀⠀⠀随着时间的推移，这种条件反射可能会导致培训师倾向于采用那些增加正确反应率的方法——也就是说，使学员的生活更轻松。这样做，当然会使培训师远离引入前面部分总结的合意困难。」

更重要的是，大多数教育机构的运作方式加剧了这一问题：

⠀⠀⠀「有一种倾向在促使教师选择培训项目来最大化训练者的表现和反应，这种倾向被现实世界组织中的某些制度特征所加剧。

⠀⠀⠀首先，那些负责培训的人自己也要接受评估，其依据往往是学员训练期间或训练结束时的表现或满意度。

⠀⠀⠀其次，负责日常培训的人通常没有机会观察他们所培训的人员在培训后的表现；学员后来的成功和失败远离原始培训环境和培训者本人的环境。

⠀⠀⠀系统性地测量培训后在职表现的情况也很少见，更不用说将这些测量结果提供给培训者作为对哪些操作能否实现培训后目标的指导。

⠀⠀⠀最后，尽管存在复习和再培训的地方，这些通常是由那些不负责原始培训的人来管理的。」

微观交错和宏观交错

| 宏观交错

Math Academy 在复习和测验中都融入了交错练习，学生在学习任务中交错处理每道练习题。而课程则包含最小量的分块练习，因为这种方法更合适用在学生初次学习新知识时。

然而，通过将我们的课程分解成大量的小型、基础的课程，我们通过这些课程采用广度优先（而非深度优先）的学习路径，实施了一定程度的交错练习。我们称之为宏观交错，与微观交错（即在单个学习任务中交错练习题）相对。

大多数资源并未利用宏观交错。例如，在典型学校中学习微积分时，学生可能会花一个月学习极限，然后一个月学习求导规则，之后一个月学习积分技巧，最后一个月学习数列和级数——这实际上是宏观分块。班级将所有时间花在一个单元上，直到宣布「完成」并转向下一个单元。为了利用宏观交错，最好将每小时的课程分成 15 分钟，分别学习四个类别中的一个小型主题。

| 微观交错

Math Academy 最大程度地利用了宏观交错。即使表面上看起来不明显。微观交错也被充分利用了。

表面上看，课程是分块练习，只能潜在地为子技能提供所需的间隔重复复习，但这些子技能需要微观交错的复习。难道不应该在每个主题出现在测验中之前进行微观交错复习吗？

然而，这实际取得了最好的平衡。

• 如果你想在每个主题中微观交错问题类型，然后再在测验中看到它们，那么你必须在测验中看到每个主题之前对其进行显式复习。
  
  
• 如果你必须对每个主题进行显式复习，那么很快你的复习就太多了，你的进度将停滞不前，因为你把所有时间都花在复习上而不是学习新材料（这是对间隔重复系统的常见抱怨）。

所以，你必须做出决定：你应该

1. 在测验前完全微观交错所有内容，还是
2. 放弃一点微观交错，以实现间隔重复优化，从而更快地学习新材料？

如果你想最大化学习效率，即学习努力转化为教育进步的速度，那么选项 2 更好。

此外，在选项 2 中，当进行重复压缩时，实际上放弃的微观交错很少。复习不仅微观交错了原课程中的问题类型，还微观交错了子（前置）技能——复习是专门选择的，旨在覆盖尽可能多的你需要练习的子技能，因此实际上你在每次复习中都会获得超量的微观交错。

关键论文

注意：「重要性」部分可能包含了本章前文中直接引用的片段。如需引用本章内容，请以正文（上文）为准。

• Rohrer, D., & Pashler, H. (2007). Increasing retention without increasing study time. Current Directions in Psychological Science, 16(4), 183-186.
  
  重要性：交错练习能为多个不同主题提供最小有效剂量的复习，而集中练习仅针对单一主题，并将大部分复习精力浪费在了收益递减的区域。
  
  
• Rohrer, D. (2012). Interleaving helps students distinguish among similar concepts. Educational Psychology Review, 24, 355-367.
  Taylor, K., & Rohrer, D. (2010). The effects of interleaved practice. Applied cognitive psychology, 24(6), 837-848.
  
  重要性：交错练习能增强辨别学习和类别归纳学习。虽然集中练习能更快地提升表现（这使其在初学技能时很有用），但交错练习能极大地促进知识的保留和迁移（这使其成为更有效的复习策略）。
  
  
• Rohrer, D. (2009). Research commentary: The effects of spacing and mixing practice problems. Journal for Research in Mathematics Education, 40(1), 4-17.
  
  重要性：通过引入间隔练习或混合练习——这也是混合复习的两个典型特征——考试分数能够得到显著提高。此外，无论是间隔练习还是混合练习，都不需要增加练习题的总量，这意味着这两种方法既能提升效率，也能增强效果。
  
  
• Bjork, E. L., & Bjork, R. A. (2011). Making things hard on yourself, but in a good way: Creating desirable difficulties to enhance learning. Psychology and the real world: Essays illustrating fundamental contributions to society, 2(59-68).
  Rohrer, D., & Hartwig, M. K. (2020). Unanswered questions about spaced interleaved mathematics practice. Journal of Applied Research in Memory and Cognition, 9(4), 433.
  
  重要性：合意困难包括：变化学习条件，而非保持其恒定和可预测；将不同主题的教学内容交错安排，而非按主题集中安排（即集中练习）；间隔安排（而非集中安排）特定主题的学习时段；将测试（而非讲解）作为学习活动。然而，人们可能未能充分利用这些有益的练习方式，因为「困难可以是合意的」这一点，并非凭直觉就能认识到。
  
  
• Bjork, R. A. (1994). Memory and metamemory considerations in the training of human beings. In J. Metcalfe and A. Shimamura (Eds.), Metacognition: Knowing about knowing (pp.185-205).
  
  重要性：就训练后的知识保留和迁移效果而言，许多最有效的训练方法都具有一个共同特点：它们会给学习者带来困难。然而，通常培训者有动机去最大化受训者的即时表现和/或满意度，这使得他们倾向于避免引入这类合意困难。更有甚者，大多数培训机构的设置往往会加剧这个问题。
  
  
• Taylor, K., & Rohrer, D. (2010). The effects of interleaved practice. Applied cognitive psychology, 24(6), 837-848. Pan, S. C. (2015). The interleaving effect: mixing it up boosts learning. Scientific American, 313(2). Rohrer, D., Dedrick, R. F., & Stershic, S. (2015). Interleaved practice improves mathematics learning. Journal of Educational Psychology, 107(3), 900.
  
  重要性：在多项研究中，仅仅是将练习题交错安排（而非集中安排），就能使考试分数翻倍或接近翻倍。此外，采用交错练习的学生在延迟一段时间后，对测试内容的记忆保留效果也表现得极为出色。
  
  
• Kornell, N., & Bjork, R. A. (2008). Learning concepts and categories: Is spacing the “enemy of induction”?. Psychological science, 19(6), 585-592.
  
  重要性：事实证明，交错练习并非「归纳学习的敌人」，尽管集中练习显然营造了一种学习顺畅的错觉：参与者评价交错练习比交叉练习更有效，即便他们自己的测试成绩已经证明了事实恰恰相反。
  
  
• Metcalfe, J., & Xu, J. (2016). People mind wander more during massed than spaced inductive learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 42(6), 978.
  
  重要性：研究发现，与进行交错练习时相比，参与者在进行集中练习时出现「走神」的情况更为频繁。

补充资料

• Carpenter, S. K., & Agarwal, P. K. (2019). How to use spaced retrieval practice to boost learning. Iowa State University.
• Rohrer, D., & Hartwig, M. K. (2023). Spaced and Interleaved Mathematics Practice. In C. Overson, C. M. Hakala, L. L. Kordonowy, & V. A. Benassi (Eds.), In Their Own Words: What Scholars and Teachers Want You to Know About Why and How to Apply the Science of Learning in Your Academic Setting (pp. 111-21). Society for the Teaching of Psychology.
• Agarwal, P. K., & Agostinelli, A. (2020). Interleaving in Math: A Research-Based Strategy to Boost Learning. American Educator, 44(1), 24.
• Atchison, K. (2020). True Mastery: The Benefits of Mixed Practice for Learning. EducationalRenaissance.com.
• Are Spacing and Interleaving the Same Thing? InnerDrive.co.uk.
• Interleaving Do’s and Don’ts. InnerDrive.co.uk.

上一章：

下一章：

Thoughts Memo 汉化组译制
感谢主要译者 claude-3.7-sonnet，校对 Shom
原文：The Math Academy Way: Using the Power of Science to Supercharge Student Learning

← 返回目录