← 返回目录

第十八章 间隔重复（分散练习）

学校≠教育≠技能；文凭溢价=80%信号传递+20%人力资本

67 👍 / 4 💬

⠀⠀⠀摘要：当我们将复习分散到多个时段（而非集中在单一时段内）时，不仅能恢复记忆，还能将其进一步巩固到长期记忆中，从而减缓遗忘。这种现象被称为间隔效应。间隔效应的一个重要推论是，完成的复习越多（在适当间隔的情况下），记忆保持的时间就越长，下次需要复习的时间间隔也就可以越长。基于这一发现，人们开发出了一种系统化复习先前学习材料的方法，称为间隔重复（或分散练习）。这里的「重复」指的是在适当时机成功进行的复习。在像数学这样有层级的知识体系中应用间隔重复是复杂的，这主要是因为高阶主题的复习会对低阶主题产生「涓滴效应」，从而使得这些主题相关的复习排期也需要改变，当然这些重复可能过早，不能算作一次完整的复习，因此需要适当地折算其效果。为了应对这一挑战，我开发了一个名为部分隐式重复 (Fractional Implicit Repetition, FIRe) 的模型。这个模型不仅考虑了隐式的「涓滴」复习，还通过巧妙选择复习内容，让某个主题的隐式复习能连带完成其他待复习主题（就像多米诺骨牌那样），从而显著减少了所需的总复习次数。更为关键的是，该模型能够根据每个学习者在不同主题上的表现，动态调整间隔重复的节奏，在学习者能力和主题难度这两个相互影响的因素之间找到最佳平衡点。

记住知识直到永远

| 间隔效应

学习新知识只是解决学习难题的一半。另一半挑战在于如何牢记所学内容。要想记住知识，必须定期复习——否则，知识终将被遗忘。

一种常用的可视化记忆遗忘过程的方法是通过遗忘曲线来展示，这一概念最早由 19 世纪末的心理学家赫尔曼·艾宾浩斯提出并研究：

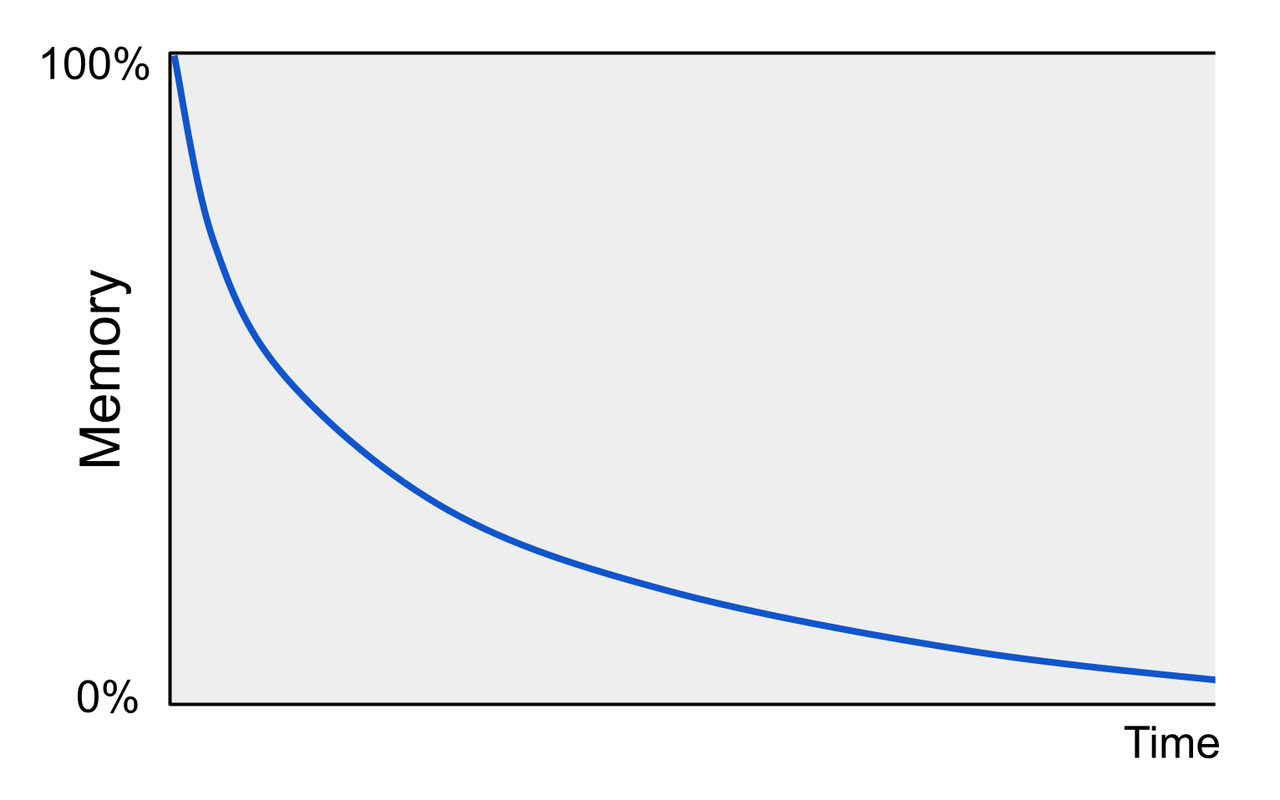
艾宾浩斯（1885）发现，当复习被间隔开来或分散到多个时间中进行（而不是集中在单一时期内）时，不仅能恢复记忆，还能将其进一步巩固到长期记忆中，从而减缓遗忘速度。这种现象现在被称为间隔效应。

| 间隔重复

间隔效应带来的一个深远影响是：完成的复习次数越多（在适当的间隔下），记忆保留的时间就越长，下一次需要复习前的等待时间也就越长。这一发现催生了一种系统复习先前学习材料的方法，称为间隔重复（或分散练习）。在这里，「重复」指的是在适当时机成功进行的复习。

下面是一个例子，用来说明间隔重复的过程和威力。假设你学习了一个新单词。起初，你可能只能记住这个单词一天。但如果你在第二天测试自己对其含义的记忆，那么你可能会记住它直到周末。如果你在周末再次进行自测，那么你可能会记住几周。如果你坚持这种间隔重复的计划，最终你将能够在两次重复之间间隔多年（Bahrick et al., 1993）。

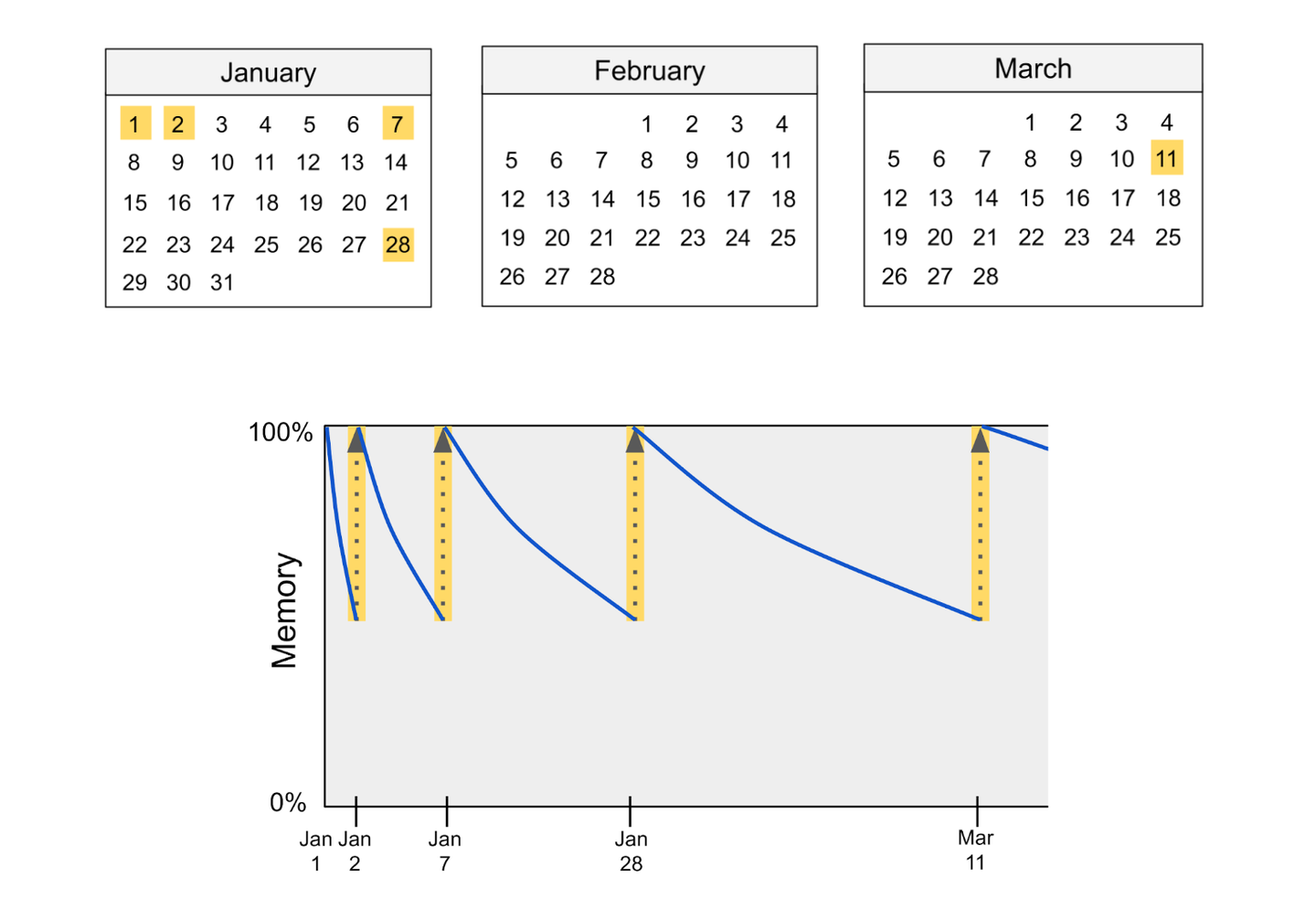
间隔重复的主要挑战在于如何选择最佳的复习间隔时间。如果间隔时间过长，你可能会遗忘所学的内容，导致你在间隔重复安排中倒退。但如果下一次复习来得过早，你的记忆强度就不会得到充分的提升，学习进度也会相应放缓。

| 直观理解间隔重复

Qadir & Imran (2018) 通过类比肌肉锻炼来解释间隔重复，帮助我们直观地理解这一概念：

⠀⠀⠀「……集中学习可能会带来暂时的熟练感，就像健身者通过密集训练可以使肌肉短时间内膨胀起来。然而，只有通过间隔锻炼，肌肉才能真正成长（即锻炼和休息交替进行）。同样，要实现长期有效的学习，也需要采用间隔练习的方，而不是依赖于突击学习。」

Brown, Roediger, & McDaniel (2014, pp.9-10, 81-82, 100-101) 对此进行了深入阐述：

⠀⠀⠀「教育工作者普遍认为，掌握新技能的最有效方法是专注且持续地练习，直到完全掌握为止。这种观念根深蒂固，因为在集中练习的过程中，我们常常能看到快速进步。然而，研究表明，这种集中练习带来的进步往往是短暂的，很快就会消退。

⠀⠀⠀……

⠀⠀⠀集中练习之所以能给我们带来掌握的感觉，是因为我们在短期记忆中不断循环信息，而不需要从长期记忆中重构学习内容。但这种方法，就像反复阅读作为学习策略一样，获得的熟练感是暂时的，掌握感也是虚假的。真正触发知识重新巩固和深度学习的，是那个费力重构知识的过程。

⠀⠀⠀……

⠀⠀⠀当你从短期记忆中回忆所学内容时，比如在快速反复练习中，几乎不需要多少脑力，这样带来的长期收益也很有限。但当你在一段时间后回忆，而对内容的掌握已经有些生疏时，你就必须努力重构它。这种费力的回忆不仅强化了记忆，还能让所学内容重新变得灵活，从而促进了重新巩固。重新巩固有助于用新信息更新记忆，并将其与近期学习的内容联系起来。」

重新巩固的过程可以类比为（第 73-74 页）多次修改一篇文章的过程：

⠀⠀⠀「大脑巩固新知识的过程，可以用写作文章的经历来形象地类比。初稿常常是粗糙而不精确的。你是在写作的过程中逐渐明确自己想表达的内容。经过几轮修改，你的文章会变得更加凝练，多余的内容也会被删除。然后你会暂时搁置文章，让思想沉淀。当你一两天后重新审视时，你要表达的内容在脑中会变得更加清晰。这时你可能会发现自己实际上在阐述三个主要观点。你会将这些观点与读者熟悉的例子和佐证材料联系起来。你会重新组织和整合论点的各个要素，使文章更加有力且优雅。

⠀⠀⠀学习新知识的过程也是如此，开始时常常感觉杂乱无章、难以掌握；最关键的内容并不总是一目了然。知识的巩固有助于组织和固化学习内容。值得注意的是，在一段时间后进行复习也能达到类似的效果。这是因为从长期记忆中检索信息不仅能够强化记忆痕迹，还能使这些记忆再次变得可塑，从而能够与新近学习的内容建立联系。这个过程被称为重新巩固。这正是[间隔]提取练习能够修改和强化学习的原理。」

| 研究者之间的共识

值得注意的是，间隔效应仍然是一个活跃的研究领域。正如 Hartwig, Rohrer, & Dedrick (2022) 所描述，除了重新巩固之外，可能还有其他因素在起作用。尽管间隔效应背后的具体机制可能仍有争议，但其效果和实用价值已经得到研究者的一致认可：

⠀⠀⠀「研究者们已经提出了多种解释间隔效应的理论（相关综述可参见 Benjamin & Tullis, 2010; Delaney et al., 2010; Dempster, 1989）。根据这些理论，间隔效应可能源于以下几种机制：编码变异性（即在两次学习之间的间隔使得上下文变化，从而提供更丰富的编码）、加工不足（即如果两次学习时间相近，第二次对材料的加工会减弱）、记忆巩固（即第二次学习受益于间隔期间发生的记忆巩固过程）或学习阶段的提取（即间隔促进第二次学习时的主动回忆）。然而，目前还没有一种单一机制能够完全解释所有与间隔效应相关的研究发现，可能需要多种机制的结合才能最好地解释这一效应（Delaney et al., 2010）。

⠀⠀⠀无论具体机制如何，间隔效应的稳定性是毋庸置疑的——它在各种学习材料、实验程序和学习者特征中都有所体现（Dunlosky et al., 2013）。对本研究而言最重要的是，间隔效应已经在众多基于课堂的随机对照研究中得到证实（例如，Seabrook et al., 2005; Sobel et al., 2011；综述见 Dunlosky et al., 2013）。此外，课堂研究还发现间隔效应在数学学习中同样有效（Barzagar Nazari & Ebersbach, 2019; Hopkins et al., 2016; Lyle et al., 2020; Schutte et al., 2015）。简而言之，大量数据表明，采用间隔练习的方法可以提高学生在延迟测试中的数学成绩。……研究文献明确指出，如果要让学生长期保持所学知识，练习应该分散在多个课堂环节中进行（Rawson et al., 2013; Rawson et al., 2018）。」

正如 Rohrer (2009) 所言：

⠀⠀⠀「……间隔效应可以说是学习研究领域中最显著且最稳定的发现之一，它似乎适用于各种学习情境。」

事实上，研究者 Kang (2016) 指出，数百项研究已经证实，间隔重复能够产生更优越的长期记忆效果。为了生动说明这一点，他描述了一项最早的间隔重复研究，其结果在过去一个世纪中被 254 项后续研究所反复验证：

⠀⠀⠀「以一项早期研究为例，研究者要求大学生学习雅典誓言 (Gordon, 1925)。他们将学生分为两组：一组连续听 6 次誓言朗读；另一组在第一天听 3 次，三天后再听 3 次。

⠀⠀⠀在即时测试中，集中学习组的表现略优于间隔学习组。然而，在 4 周后的延迟测试中，间隔学习组的表现明显优于集中学习组。

⠀⠀⠀这一结果表明，尽管集中练习在短期内可能看似[略微]更有效，但间隔练习才能产生持久的长期学习效果。」

间隔学习的效果如此显著和确凿，以至于它引起了广告领域的高度关注。在这一领域中，众多研究已经复现了间隔效应在增强消费者对品牌记忆方面的有效性 (Schmidt & Eisend, 2015)。

间隔重复未被充分利用

不幸的是，和精熟学习法一样，间隔重复偏离了教育中的传统惯例，因此在课堂上很少被使用。正如 Kang (2016) 所感叹的：

⠀⠀⠀「尽管一个多世纪以来的研究结果已证明了间隔效应，但它在课堂上的应用并不广泛。间隔效应是『心理学研究成果未能有效应用的一个案例』（Dempster, 1988, p. 627）。

⠀⠀⠀……

⠀⠀⠀在选择使用哪种教学技术（以及何时使用）时，许多教师倾向于采用熟悉的方法（例如，他们自己曾经接受的教学方式；Lortie, 1975）或依赖直觉，而这些方法并不理想：我们对学习的直觉有时可能完全错误，而忽视关于各种教学或学习策略有效性的不断增加的证据将是一种浪费。

⠀⠀⠀……

⠀⠀⠀第二个主要障碍是传统的教学实践，它通常偏向于集中练习。教学材料和辅助工具（例如，教科书、练习册）通常以模块化方式组织，这使得集中练习变得方便。在课堂上介绍新主题后，教师通常通过作业让学生进行该主题的练习。然而，除了在介绍主题后不久的那段练习之外，通常没有后续的练习，直到在重大考试前的复习课。」

或许令人惊讶的是，Cepeda et al. (2009) 发现，即便是许多教学设计和教育心理学的教材也几乎没有提到间隔重复作为一种学习策略：

⠀⠀⠀「在教学设计和教育心理学的教材中，明显忽视了分散练习的研究，许多教材甚至没有提到分散练习效应（例如，Bransford, Brown, & Cocking, 2000; Bruning, Schraw, Norby, & Ronning, 2004; Craig, 1996; Gardner, 1991; Morrison, Ross, & Kemp, 2001; Piskurich, Beckschi, & Hall, 2000）。

⠀⠀⠀那些提到分散练习效应的教材通常只用一个段落或更少的篇幅来讨论这一主题（例如，Glaser, 2000; Jensen, 1998; Ormrod, 1998; Rothwell & Kazanas, 1998; Schunk, 2000; Smith & Ragan, 1999），并且在学习环节之间的间隔时间应该有多长的问题上提供了截然不同的建议——其中很多是错误的（参见 Gagné, Briggs, & Wager, 1992; Glaser, 2000; Jensen, 1998; Morrison et al., 2001; Ormrod, 2003; Rothwell & Kazanas, 1998; Schunk, 2000; Smith & Ragan, 1999）。」

通常，学生在课堂上学习一个主题，在做作业时进行练习，然后就将其遗忘，直到需要为考试复习。考试之后，除非有新主题需要他们记住旧知识，否则学生很少被要求再次练习该主题。最终，学生往往会忘记大部分所学内容——正如 Rohrer (2009) 所指出的，遗忘可能如此严重，以至于看起来他们从未学过这些东西：

⠀⠀⠀「遗忘的影响常常被学习理论家忽视，但如果材料不能被记住，习得就没有太大意义。确实，虽然标准化测验中的糟糕表现常被归因于缺乏学习，但遗忘往往是罪魁祸首。

⠀⠀⠀例如，在 1996 年的国家教育进展评估中，50% 的美国八年级学生无法正确计算 -5 和 -7 的乘积，尽管问题是以选择题形式呈现的（Reese, Miller, Mazzeo, & Dosse, 1997）。很有可能这些出错的学生中有任何人以前知道这个乘积，遗忘往往是罪魁祸首。」

通常，学生在缺乏间隔复习时，甚至意识不到自己遗忘得有多快。例如，Emeny, Hartwig, & Rohrer (2021) 发现，参与间隔练习的学生能够相当准确地预测他们未来的考试成绩，而进行集中练习的学生则对自己的预测过于自信：

⠀⠀⠀「在间隔练习后，学生对未来考试成绩的预测非常准确，而集中练习则导致严重的过度自信。集中练习后的过度自信可能源于学生通过重复相同步骤解决一组类似问题时的流畅性或成功率，这给他们一种已经掌握内容的错觉。反过来，过度自信可能让学生和教师误以为不需要进一步练习，而实际上，这些学习成果并不会长久保留。

⠀⠀⠀尽管集中练习导致了过度自信，我们注意到，集中练习后的预测仅比间隔练习后的预测略高。因此，集中练习并没有让预测达到不切实际的高水平，而是未能帮助学生认识到他们的掌握水平较低。」

将间隔重复排除在 STEM 课堂之外的另一个因素是，据我们所知，当前关于确定最佳复习间隔的数学模型研究，仅限于独立的类似抽认卡的学习任务场景。相比之下，STEM 科目是高度互联的知识体系。这带来了显著的建模复杂性：例如，对于高级主题的重复应该「涓滴」，以更新那些被隐式练习到的基础主题的重复规划（同时要适当折扣，因为这些复习通常发生得过早，在效果上不能完全算作下一次正式复习）。

为了克服这个障碍，我在 Math Academy 开发了一个部分隐式重复 (Fractional Implicit Repetition, FIRe) 模型。这个模型不仅考虑了隐式的「涓滴」重复，而且还

我们的这个精密复杂的间隔重复模型是自 2019 年以来，经过多年研究、实践和开发的成果。随着我们不断积累更多学生学习成果的数据，这个模型还在持续优化和完善中。

间隔重复提高泛化能力

人们通常认为间隔重复只能用来记忆孤立信息。但对于像数学这种大量复杂技能高度关联的学科，间隔重复也可以促进更加泛化的学习，使其更容易在不同情境中应用。

先从一些简单的直观感受开始，想象一下当你重读一本书，或者重看一部许久未看的电影时会发生什么。你往往会注意到之前未曾留意的细节。与你上次观看时相比，你开始时的心态有了变化，而结束后你也会得到新的观点，以及对作品更全面的理解。

事实上，Smith & Scarf (2017) 回顾了多项研究，证明「间隔不仅有助于特定项目的学习和记忆，还改善了学习的泛化」：

⠀⠀⠀「Hagman (1980) 的研究让参与者在相同或不同设备上学习和练习电气测试，练习集中在一天内完成或分散在连续三天内。在 2 周延迟后的迁移测试中，在不同设备上进行的间隔练习比在相同设备上进行的间隔练习效果更好。在相同设备上进行的间隔练习在迁移测试中的表现优于在相同或不同设备上进行的集中练习。此外，在相同或不同设备上进行的集中练习在迁移测试中的表现相当，这表明间隔对于训练变化以促进泛化是必要的。

⠀⠀⠀同样，Moulton et al. (2006) 比较了在 PVC 动脉模型和火鸡大腿动脉上练习显微外科技能的集中训练组和间隔训练组，并测试了他们的技能在训练后 1 个月内转移到活体大鼠的程度。Moulton et al. (2006) 发现，间隔训练组在多项结果测量上明显优于集中训练组。

⠀⠀⠀针对儿童的研究探讨了间隔对泛化的影响，使用了比成人研究更广泛的间隔时间。例如，Vlach 和 Sandhofer (2012) 研究了间隔对 5 至 7 岁儿童简单和复杂科学概念泛化的影响。参与研究的儿童完成了 4 节关于生物群落的课程，每节课涉及不同的背景（沙漠、草原、北极、海洋或沼泽），并在最后一节课后一周进行后测。集中组在 1 天内完成了所有四节课，中间组在 2 天内每天完成 2 节课，而间隔组在 4 天内每天完成 1 节课。对于简单泛化，间隔组在前测到后测的进步显著大于集中组，而中间组的进步与集中组或间隔组相比没有显著差异。相反，对于复杂泛化，间隔组的进步显著优于集中组和中间组。事实上，数据表明，间隔组是唯一一个在问题从简单到复杂时显示出进步的组，尽管这一趋势没有进行统计显著性检验。因此，间隔可能为更复杂的泛化提供更大的益处。

⠀⠀⠀Gluckman et al. (2014) 重复了 Vlach 和 Sandhofer (2012) 的发现，但在后测中，他们除了泛化问题外，还加入了关于儿童在课程中谈论的事实和概念的记忆问题（例如，什么是生物群落？）。对于简单和复杂的泛化问题以及记忆问题，间隔组显示出显著大于集中组的进步。报告的平均值显示了与上述相同的模式，间隔对复杂泛化的益处大于简单泛化。」

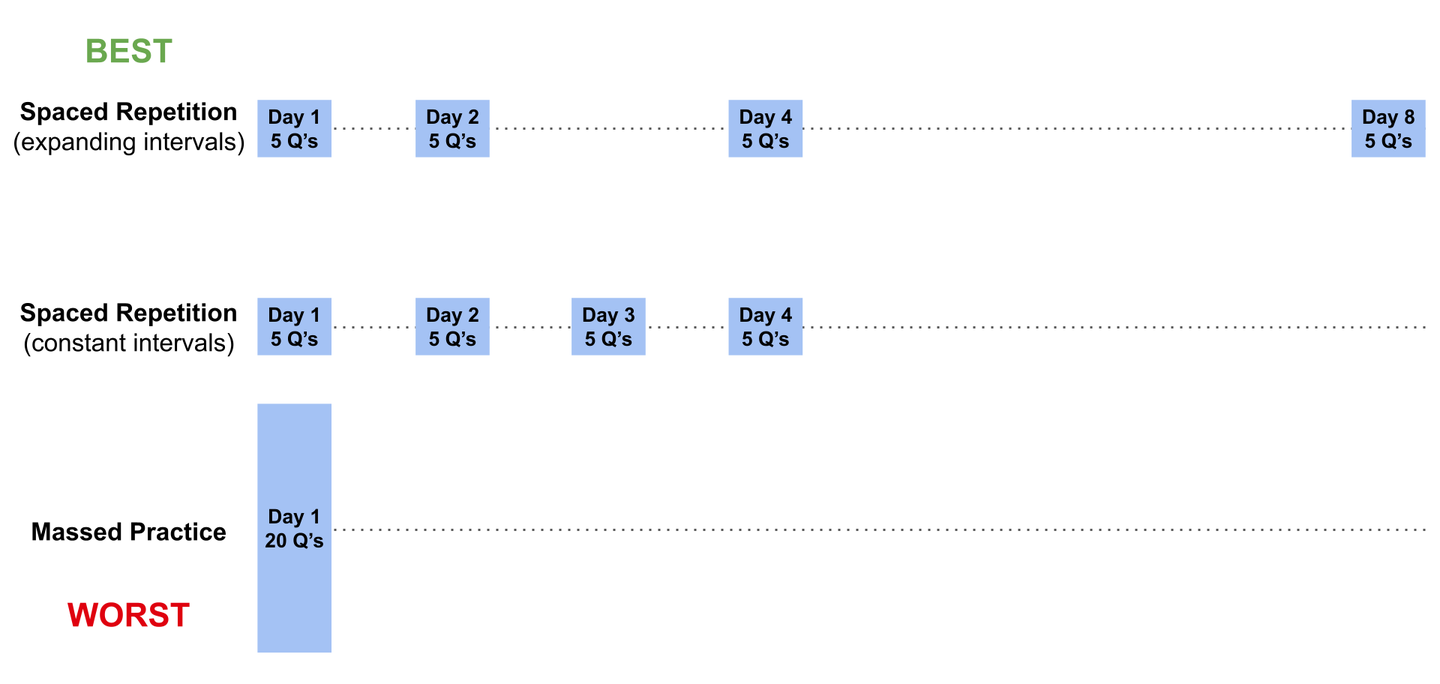
在后续研究中，Vlach, Sandhofer, & Bjork (2014) 还发现，与恒定间隔的间隔重复相比，采用递增间隔的更优效果的间隔重复更能促进泛化，这表明优化间隔重复过程可以显著提升泛化能力：

⠀⠀⠀「……我们研究了递增间隔学习排期是否会比等间隔学习排期更有效地促进泛化……在 24 小时延迟泛化测试中，我们观察到两种条件之间存在显著差异：递增间隔条件下的儿童表现明显优于等间隔条件下的儿童。

⠀⠀⠀……

⠀⠀⠀这些发现表明，递增间隔的益处不仅限于记忆任务，这些学习规划还可以促进多种类型的学习，例如信息的习得和泛化。」

压缩重复次数

一个对间隔重复的常见批评是它需要的复习量太大了。这种批评在使用间隔重复学习互不相关的抽认卡时可能成立，但在数学学习中，数学学科的特殊性让 Math Academy 能够规避这个问题。

与孤立的抽认卡不同，数学是一个层次分明、高度关联的知识体系。当学生解决一个高级数学问题时，他们实际上在潜移默化中练习了许多基础数学技能。换言之，在数学领域中，高级技能往往包含了众多基础技能。

因此，当学生需要进行复习时，Math Academy 能够将复习任务压缩成一个规模更小的学习任务集。这个精简的任务集能够隐式包含（即重复练习）所有待复习的内容。我将这个过程称为压缩重复（repetition compression）。

为了更好地阐述这个概念，让我们看一个具体的乘法例子，即将两位数 39 乘以一位数 6：

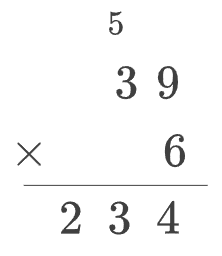
要完成上述乘法运算，我们必须对一位数字进行乘法运算，并将一位数字加到两位数字之上：

换句话说，「两位数乘以一位数」这个运算实际上包含了「一位数乘法」和「一位数与两位数的加法」这两个基本运算。

我们可以通过下面的包含图来可视化这种关系。包含图与前置知识图类似，但有一个重要区别：这里的箭头表示一个较简单的主题被一个更高级的主题所包含。（需要注意的是，被包含的主题通常是前置知识，但并非所有前置知识都会被完全包含。）

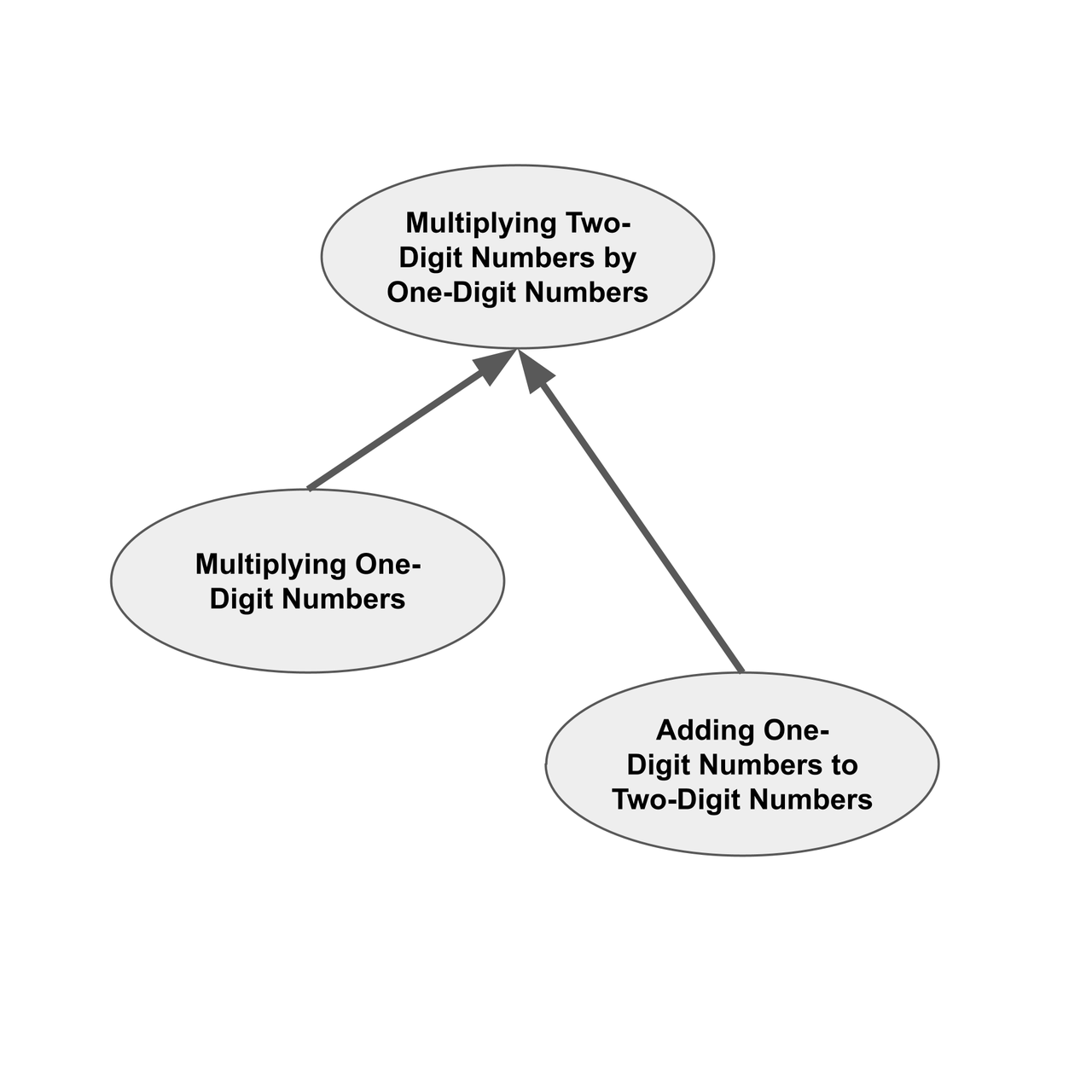
现在，假设一个学生需要复习这三个主题。由于知识间存在包含关系，他们实际上只需要复习「两位数乘以一位数」这一主题。当完成这个复习时，学生也在练习了这些技能，从而隐式重复了其包含的主题。

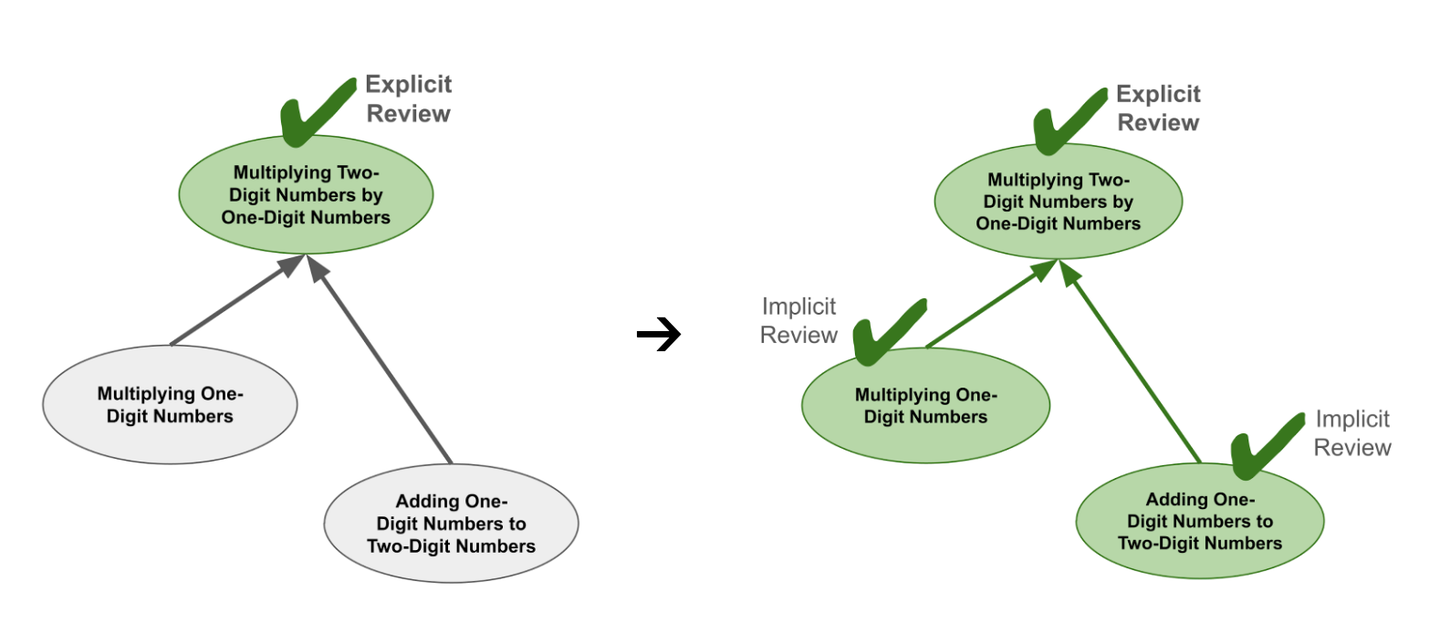
一般而言，知识之间的包含关系越多，实际需要的复习就越少。而数学恰恰是一个存在大量包含关系的学科！

因材施教，适应学生个体差异和主题特性

如第七章[1]所述，学生在学习速度和记忆所学内容的能力上存在差异。研究表明，学生之间在学习速度和记忆保持能力上存在显著差异：有些学生学习快、记忆久，而另一些则学习慢、遗忘快（例如，Kyllonen & Tirre, 1988; Zerr et al., 2018; McDermott & Zerr, 2019）。同样，不同主题的学习难度也各不相同：简单的主题往往学习速度快、记忆持久，而困难的主题则需要更长的学习时间，且更容易被遗忘。

因此，每个学生在每个主题上的学习速度都是由学生个人能力和主题难度这两个因素共同决定的。Math Academy 会计算这些学生在特定主题上的学习速度，并据此调整间隔复习的过程。

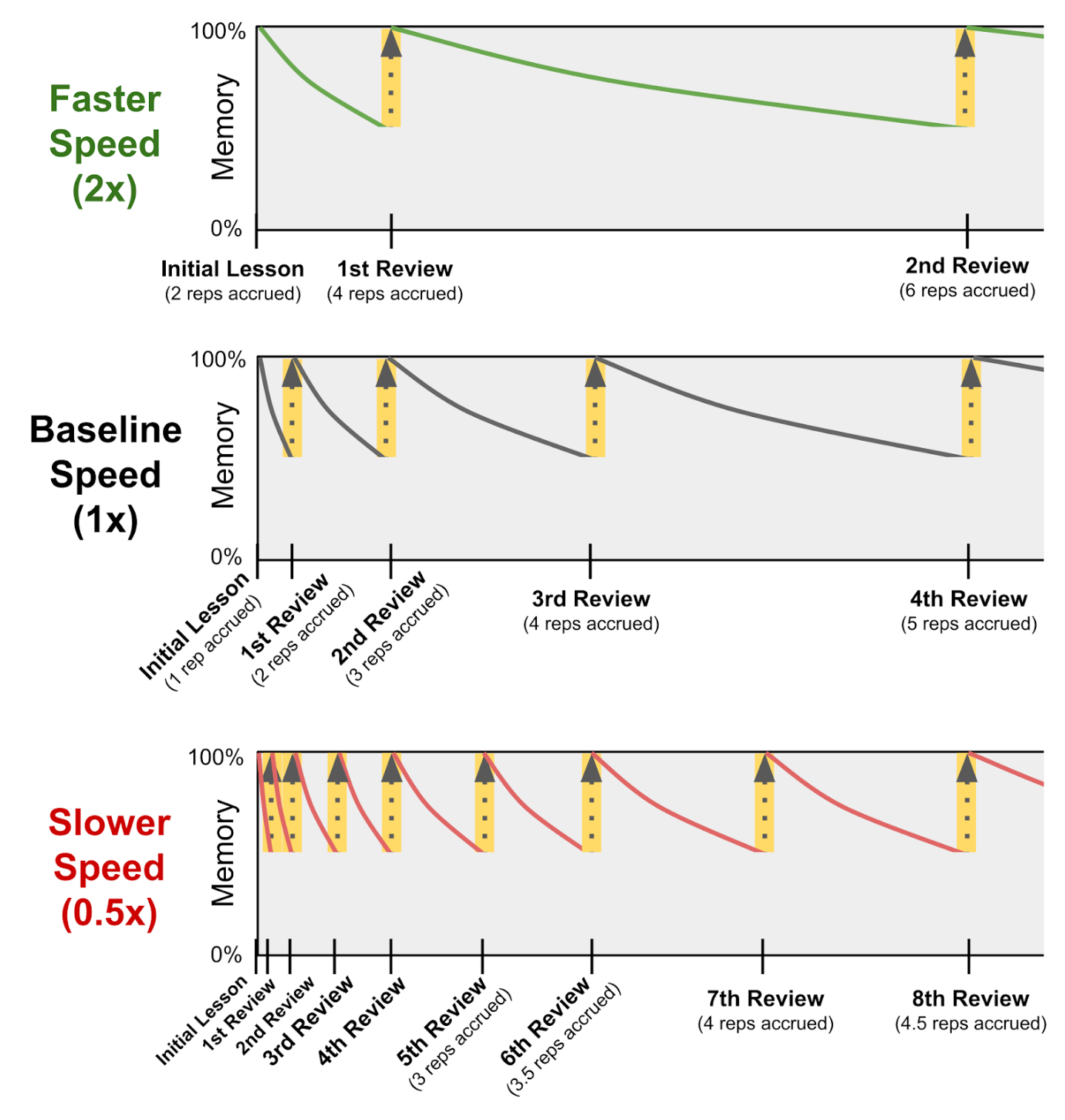
在部分隐式重复算法中，也会考虑「学生-主题学习速度」这一因素。因此，当需要放慢某个主题的间隔重复进度时（即当该学生在这个主题上的学习速度低于标准水平时)，最佳策略是取消所有即将到来的隐式重复得分，转而强制进行显式复习。换句话说，这个主题将不再接收原本应该从更高级主题「涓滴」的隐式重复得分。

之所以这样做，是因为在实际中，学习能力较弱的学生通常难以在复杂主题上获得隐式重复的学习效果——他们更难理解「我之前学过的内容是我现在学习内容的一个特例（或组成部分）」这种关系。根据学生在特定主题上的学习速度来决定是否需要强制进行显式复习是合理的。这是因为当某个主题的间隔重复过程变慢时，通常表明该主题对学生而言相对较难掌握。

最后，我们需要认识到，虽然诸多因素可能影响学生的学习速度，如天资、遗忘速率、兴趣或动机水平，以及学习时的疲劳程度或注意力分散等，但这些因素最终是否重要，只取决于它们对学生实际表现的影响。而我们正是依据这些实际表现，来调整适合每位学生的个人学习曲线。

间隔重复与螺旋式教学

一些课程采用螺旋式教学方法，在后续的教材章节和/或年级中自然地重温和深化学习内容。与缺乏系统性复习的传统教学模式相比，螺旋式教学显然是一种改进——它允许教师在没有技术辅助的情况下，在小组层面进行手动教学时，在某种程度上利用间隔效应。然而，螺旋式教学仍未达到实现真正间隔重复最大效益所需的细致、精确和个性化水平。

请注意，虽然螺旋式教学有时与发现式学习混为一谈（两者在 1960 年代被广泛归功于心理学家 Jerome Bruner），但这实际上是两个独立的概念，我们并不打算支持后者。有许多螺旋式课程（例如，Saxon Math）利用直接指导而非发现式学习。这里的讨论仅限于螺旋式教学在多大程度上利用了间隔效应，而非教学方法本身。

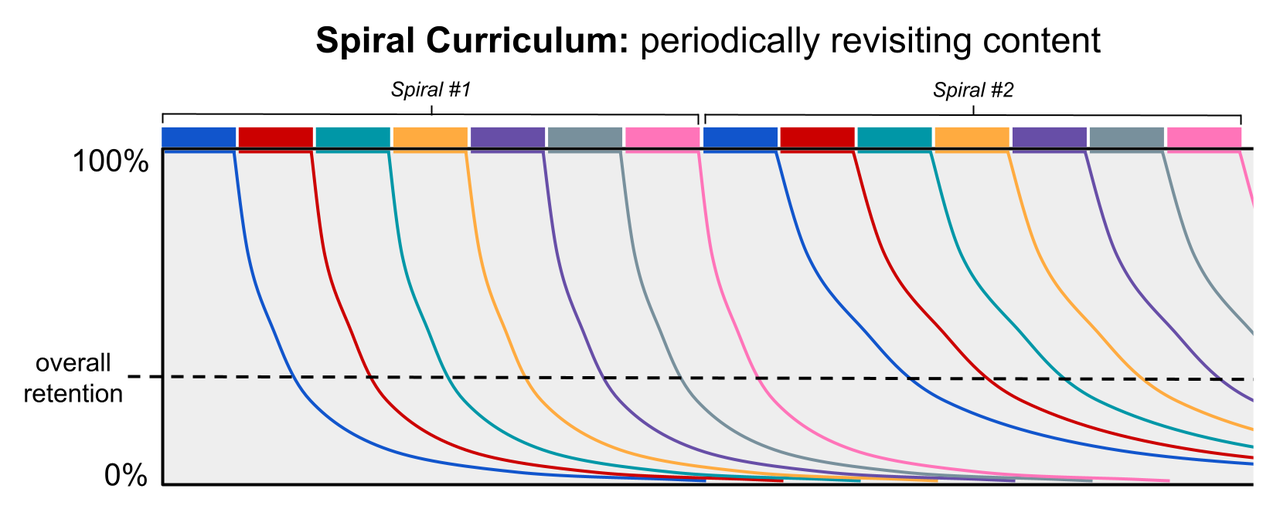
要理解螺旋式教学与间隔重复之间的区别，最好从遗忘曲线的角度来进行可视化比较。我们从传统的教学模式开始，其中大量相关材料一次性教授，而之后并没有系统性地复习。在这种教学模式下，学生很快就会遗忘所学内容，他们的整体记忆保持率极低。

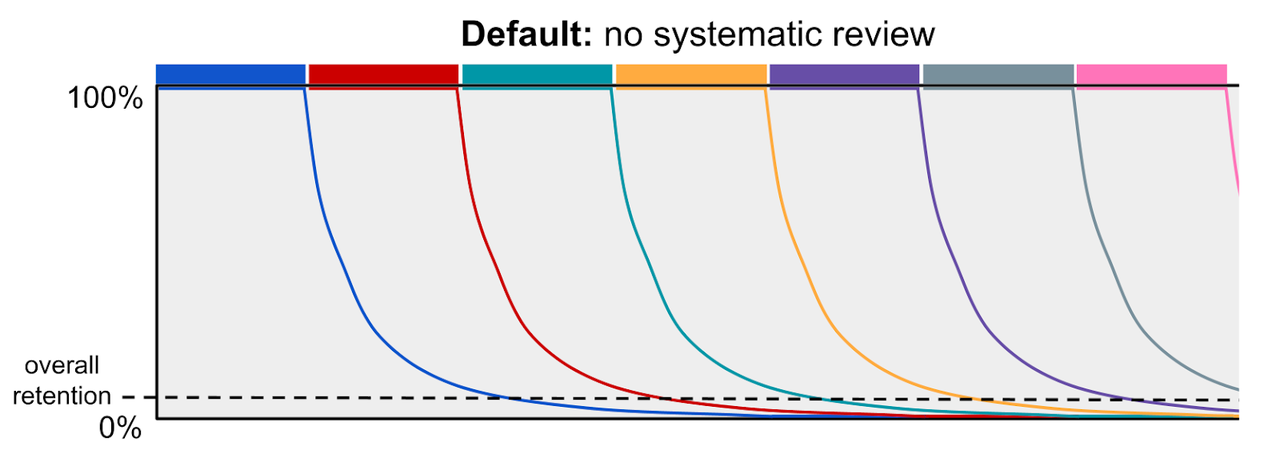
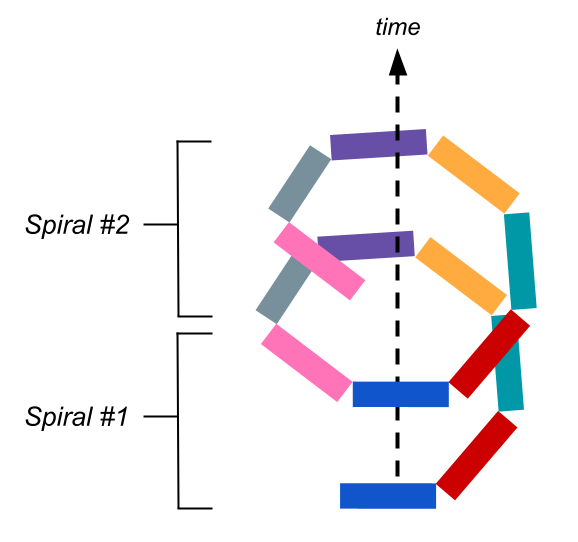
通过定期重温内容，螺旋式课程能够恢复被遗忘的知识，并利用间隔效应来减缓知识的流失。这提高了学生对所学内容的整体记忆力。为说明这一点，下面展示了一个具有两个螺旋的螺旋课程的遗忘曲线：

间隔重复将这种思路发挥到极致，通过完全优化复习过程。它精确地调整复习的间隔，以保持一致的高水平记忆力，并尽可能快地减缓衰退（即拉长衰退曲线）。复习间隔不断根据学生的表现进行调整，表现好时间隔延长，表现差时间隔缩短。通过将复习过程优化到极致，间隔重复进一步提升了学生对已学知识的长期记忆效果。

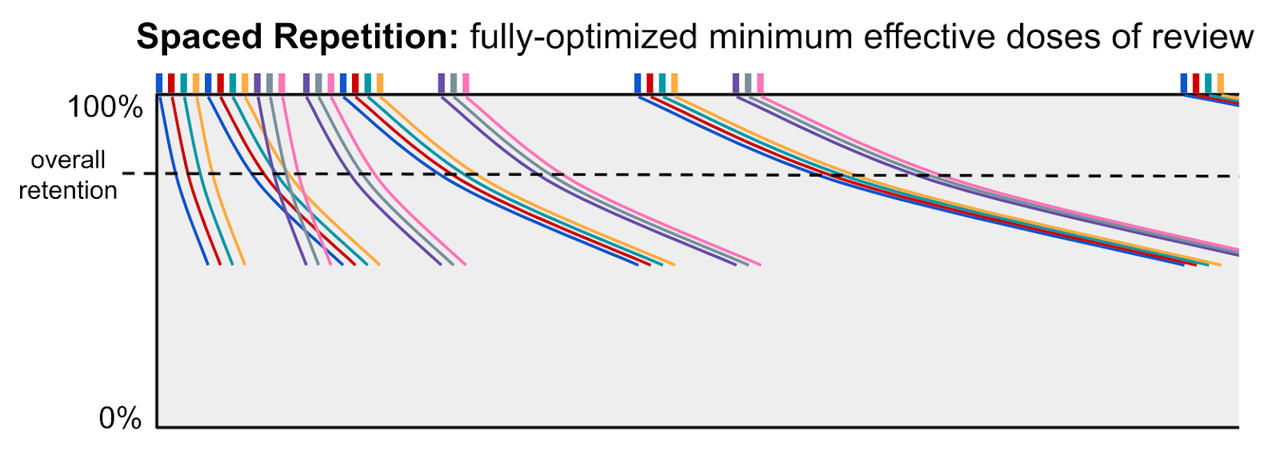
然而，虽然间隔重复更为理想，但它对教师的工作量要求非常高。若要将其真正落实到，间隔重复要求教师为每一个学生的每一个知识点建立复习计划表，并根据学生的学习表现不断更新这些计划表——而且每次学生学习（或复习）一个高级主题时，他们实际上是在隐含地复习许多更简单的主题，所有这些主题的重复计划都需要因此进行调整。

从这个角度来看，螺旋式教学可以被视为在没有技术辅助的情况下，教师在小组层面教学时「能做到的最好」。间隔重复是最大化记忆力的最佳解决方案，但手动执行间隔重复是不可行的，因此螺旋式教学是教师在没有技术辅助的情况下可以实际执行的次优选择。

关键论文

注意：「重要性」部分可能包含了本章前文中直接引用的片段。如需引用本章内容，请以正文（上文）为准。

补充资料

上一章：

Thoughts Memo：第十七章 避免干扰

下一章：

第十九章 交错练习（混合练习） - 知乎


Thoughts Memo 汉化组译制
感谢主要译者 claude-3.7-sonnet，校对 bstiat
原文：The Math Academy Way: Using the Power of Science to Supercharge Student Learning

参考

1. 第七章 个体差异：学习过程中的迷思与现实 ./24164944495.html

专栏：The Math Academy Way

← 返回目录