学校没这个能力知道吗。课堂教学 == 最低效的教学。究其原因,每个学生都有独特的知识结构,而且会随着时间自然分化,靠几个老师人力安排学习,根本不可能实现。
以下内容节选自 @Thoughts Memo 《第二十三章 利用认知学习策略需要技术》
若为王室授课:如果你的生命取决于教学成果,你会如何教学?
上述问题并非无法通过人工方式解决。每个问题都有解决方案,但这些方案需要教师付出大量努力。虽然没有任何客观规律阻止教师付出这样的努力,但现行的问责制度和激励机制不足以促使教师这样做。
(我们再次强调,这不是教师的过错,他们只是身处一个缺乏有效问责和激励机制的职业环境中的受害者。如果知道额外努力不会获得奖励,而平庸工作也不会受到惩罚,谁会愿意付出不必要的努力呢?没有人会。)
为了直观理解问责制和激励措施的重要性,不妨想象自己处于一个生死攸关的教育情境中,其结果取决于你能否有效地教导学生,使他们能够毫无疑义地向第三方证明自己的学习成果。以下是 Jason Roberts 的「辅导国王的孩子」轶事的重述:
⠀⠀⠀假设你是中世纪时期的一名教育者,在世界上最富有但也最凶狠的国王的王国中工作。国王的孩子在王国的学校就读,但国王对结果感到不满:孩子上学已经超过一年,学会了如何计数,但仍然无法解决任何需要简单运用算术的问题。
⠀⠀⠀一天,国王突然下令,要求你立即前往王座觐见。当你匆忙赶到时,国王命令你在接下来的一个月内只做一件事——教授他的孩子基础算术。这个孩子将每天与你一起学习,而在整整一个月后,国王会对他的孩子进行测试:提出五道题目,每题都要求对两个一位数或两位数进行加、减、乘、除。孩子将有两分钟时间完成每道题,而他在这次考核中的表现将决定你的命运。
⠀⠀⠀作为世上最富有的国王,他已经决定,如果孩子能在五道题中至少答对四题,那么他将赏赐你一笔数额惊人的财富,足以让你余生都能享受如同小国君主般的奢华生活。然而,如果孩子只答对三题或更少,那么你将在第二天被处决。
在这种情况下,你自然会有强大的动力去克服之前提到的所有教学障碍。整个教学体验完全以学生为中心,最大限度地利用各种可能的认知学习策略。
⠀⠀⠀突然间,你意识到你已经完全不在乎为了让这个孩子学会算术而需要付出多少时间、精力和承受多大压力。你的个人感受已经完全被抛在脑后。唯一重要的是这个孩子能否牢记算术知识,能否深入理解各种运算的含义以便在解题情境中正确应用,以及能否快速准确地计算出任何涉及两位数以内数字的算术题目。
⠀⠀⠀为了实现这个目标,你与孩子在一起的每一刻都将全心投入,帮助他独立掌握这些能力。
⠀⠀⠀• 你当然会介绍每项技能并进行简短示范,但你不会在无关事项上浪费时间,因为你的核心目标是让学生能尽可能快地开始实践,亲自解决与每项技能相关的问题。
⠀⠀⠀• 你将为学生解决的每一个问题提供详细反馈,当他们犯错时,耐心引导他们理解正确的解题思路。如果他们表现出色,你会及时引导他们挑战更高难度的问题;但如果他们遇到困难,你会提供充分的练习机会,确保他们完全掌握该技能后再继续新的学习内容。
⠀⠀⠀• 你将每天安排多元化的学习主题,并持续提供先前所学技能的复习题(但不过度复习——只提供「最小有效剂量」,恰好足以唤醒他们对可能正在淡忘主题的记忆)。
⠀⠀⠀• 你还将定期组织各种题型的限时测验,与学生一同分析测验结果,针对他们在测验中的不足之处提供针对性练习,并安排重新测试以确保他们能从错误中真正学习进步。
⠀⠀⠀• 最后,你将通过游戏化的学习方式激励孩子,让他们始终保持全力以赴的学习热情。
学生知识结构的异质性
| 辅导国王的孩子 vs 教导众多国王的孩子
「辅导国王的孩子」这一生动比喻表明,并非客观规律阻止教师为单个学生提供最优质的学习体验——这更多是关乎责任感和激励机制的问题。
然而,这个故事中有一个关键假设:老师只面对一名学生。如果将同样的故事置于一个有 30 个孩子的班级,每个孩子都来自一位国王,而每位国王都会因自己的孩子考试失败而处决老师,那么这将展现出一个截然不同的视角:无论老师多么竭尽全力,他们都无法为班级中的每一位学生提供同样完美的学习体验,因此老师可能注定失败。无论问责制多么严格、激励措施多么到位,所需的工作量都已超出了人类所能承受的范围。
简而言之,这归结为学习的基本规律。教导 30 名学生比教导单个学生难度大得多的原因在于,这 30 名学生都拥有独特且各不相同的知识结构。
| 背景知识的差异
在前置数学课程中获得不同成绩的学生,通常在进入下一门课程时带着截然不同的知识基础。例如,在前置课程中获得 C 级成绩的学生,往往比获得 A 级成绩的学生有更多的基础知识缺口(尽管即使是获得 A 级成绩的学生通常也存在一些基础知识空白,只是这些空白往往较少且/或不那么严重)。
更为微妙的是,即使在前置数学课程中获得完全相同成绩的学生,彼此之间的知识结构也常常大相径庭。两名在前置课程中掌握了相同数量知识的学生,在他们未能掌握的内容上可能完全不同。一个学生可能在理解分数时遇到困难,而另一个则可能在理解小数时感到棘手。一个学生可能在解方程时感到吃力,而另一个则可能在绘制函数图像时遇到障碍。
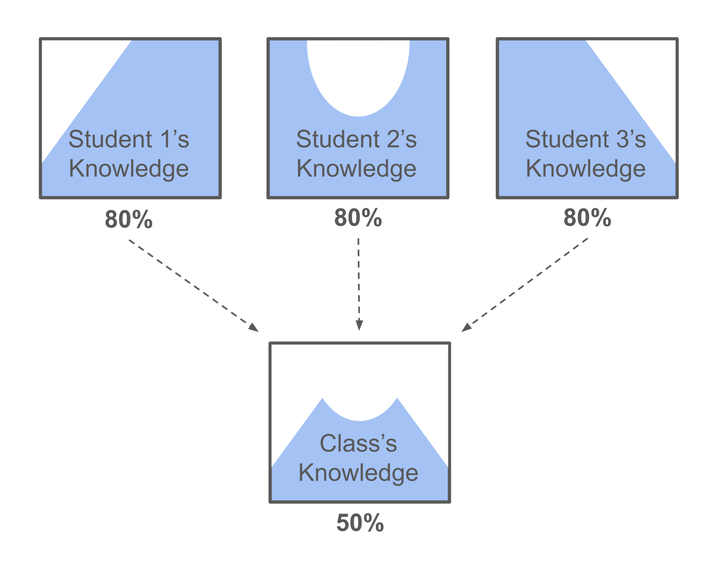
| 学生知识结构自然趋向多样化
即使在一个不切实际的假设情境中,班级里所有学生都是彼此的学业「复制品」,拥有完全相同的知识结构、学习速度和学习动机,随着课程的进行,他们的知识结构也会随着时间自然地呈现分化。尽管拥有相同的学术背景,每个学生会在不同时间缺课或走神,这导致某些学生在特定主题上比他人遇到更多困难。(缺课和走神本质上是同一回事,只是时间尺度不同:它们仅在频率和持续时间上有所区别。)
每个人都会有走神的时候——即使是成年人也不例外。这种情况频繁发生,哪怕是那些有意识地试图保持专注的人也会如此。当人们脑海中有其他事情时,很难保持专注:比如思考午餐要吃什么,周末的计划,对个人关系的焦虑等等。本书作者在撰写本小节的四段文字时也至少走神了两次。
对于学生来说尤为如此,他们在教室里还面临着无数微小干扰。例如,一个学生可能需要花 30 秒钟翻找背包寻找另一支笔或一张纸(或者被朋友借用这些物品)。又或者,一个学生可能需要离开课堂几分钟去上洗手间。
无论是否出于他们自身的原因,学生会在不同时间短暂分心,因而错过一些内容。这些差异会随着时间不断累积,除非教师能在问题出现的瞬间立即发现并完全补救——但这需要超出人类能力的工作量,所以除非教师有能实现这一点的技术支持,否则他们无法做到这一点。
| 班级中的每个学生实际上都需要一位私人导师
学生知识结构的多样性意味着不同学生在不同时期需要针对不同技能进行不同量的练习。因此,要为班级中的每位学生提供最佳学习体验,教师必须有效地扮演每个学生私人导师的角色。不言而喻,无论教师如何努力,只要班级规模超过几名学生,这就成为一个无法攻克的难题。即使教师竭尽全力,也无法为班级中的每位学生提供最佳的学习体验。
要充分运用本书探讨的认知学习策略,并为班级中的每位学生提供最佳学习体验,每个学生都需要全身心投入到有效的问题解决活动中,获得即时反馈(必要时包括补救性支持),专注于特定类型的问题,并在特定的学习情境中(例如,有参考资料与无参考资料的环境、集中式与交错式练习、限时与不限时条件),以最能促进其个人学习进步的方式学习。这一过程需要贯穿整个课堂时间,唯一的例外是学生接触新主题时,在开始主动解决问题前观察示范案例的那些短暂时刻。
然而,当学生拥有多样化的知识结构时,要找到一种对班级所有学生都有效的问题类型,即使在最理想的情况下也极为困难,而在最糟糕(也是最常见)的情况下则完全不可能。即使教师选择了他们认为适合「班级平均水平」的问题类型,对许多学生来说往往过于困难,对另一些学生而言又过于简单(无论是哪种情况,对这些学生而言都是时间的无效利用)。
要想掌握每位学生需要针对性练习的具体问题类型,教师必须单独追踪每个学生在各种问题类型上的进展,管理每个学生何时需要复习各个主题的间隔重复计划,并根据学生表现不断更新这些计划(这极其复杂,因为每当学生学习或复习一个高级主题时,他们实际上也在隐性地复习多个基础主题,所有这些主题的重复规划都需要根据学生的表现进行相应调整)。这种记录和计算工作量已经超出了人类能力范围。
此外,即使在极少数情况下,教师成功找到了对全班学生都有效的问题类型,不同的学生仍然需要不同数量的练习才能掌握解题技巧。有些学生领悟很快,仅需解决几个同类型问题就能准备好迎接更具挑战性的问题;而其他学生则需要多次尝试才能独立成功地解决给定类型的问题。另外,有些学生解题速度快,而其他学生则需要更多时间。
在缺乏技术支持的情况下,一位教师单独面对一个班级里知识水平参差不齐的众多学生时,不可能为每个人提供最佳的学习体验,因为学生们需要解决不同类型的问题并在每次尝试后获得即时反馈。然而,技术的引入彻底改变了这一切。Math Academy 通过自动化地充分利用认知学习策略,能够为每位学生提供优化的、自适应的、个性化的学习体验。在 Math Academy 平台上,学生们持续参与高效的问题解决过程,获得即时反馈(在必要时提供针对性辅导),专注于那些最能促进他们个人学习进步的特定类型问题(并在最适合他们的特定学习环境中)。
上一章:
Thoughts Memo:第二十二章 游戏化下一章:待发布
Thoughts Memo 汉化组译制
感谢主要译者 gemini-2.5-pro-exp,校对 bstiat
原文:The Math Academy Way: Using the Power of Science to Supercharge Student Learning
