优秀学生们是如何利用高效记忆法来快速掌握知识的？

问题描述

身边学霸能轻松记住大量信息，好奇他们有何秘籍？

没有什么秘籍，间隔重复罢了。这在学习科学、认知科学领域已经是人尽皆知的高效记忆方法了，我也是做间隔重复记忆算法研究的，深知一个合理的间隔重复记忆规划能提高多少学习效率。

以下我从个人轶事、学习理论、实证研究和数学建模四个方面证明间隔重复的有效性。

个人轶事（样本量=1）

在知乎大家都喜欢读故事，这很正常，人类都是喜欢读故事，最低 0.3 元每天的故事除外（逃

对我而言，间隔重复就是帮助最大的记忆方法，没有之一。我从高二下开始使用间隔重复来记忆英语单词、生物和化学的知识点等等，一年多时间成绩提高了一百多分，最后考上了哈尔滨工业大学深圳校区计算机专业，战绩可查：

你想知道如何高考逆袭吗？看我用 Anki 从本一线上涨 157 分！

间隔重复一点也不神秘，只需要做两件事：第一，将学到的知识做成能给自问自答的形式；第二，合理安排每个知识的复习时间。以下是我当年用来自测的卡片：

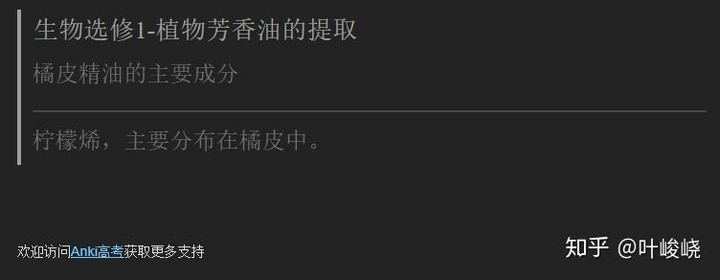
当时我差不多每天花 40 分钟到 1 个小时在间隔重复上，每天都要自测三四百个知识点：

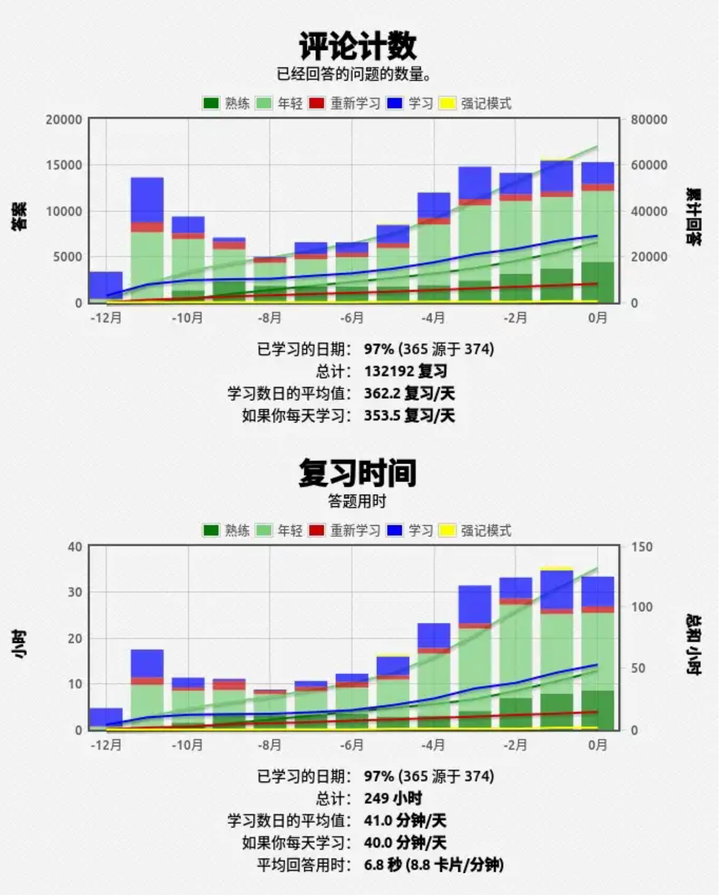
一年多时间总共记了一万五千多张卡片：

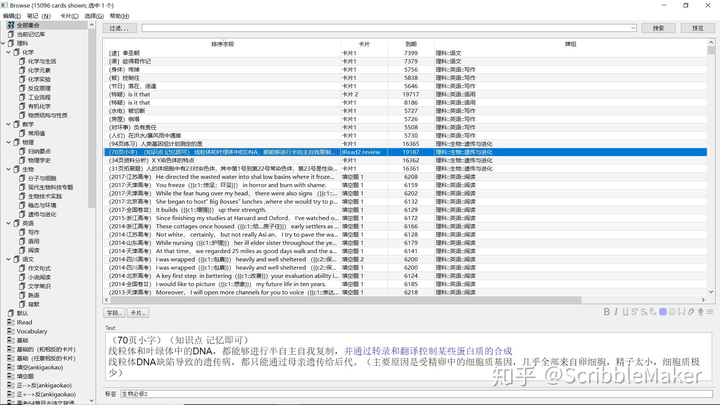
我的记忆保留率差不多在 90% 左右，也就是说这上万张卡片里面至少有 90% 是我记住的：

高考作为一个基于课纲和考纲的考试，它的知识点一定可以被穷尽的。那么，将所有知识点梳理出来，并规划一个合理的学习路径，再配合上间隔重复，肯定是可以在高中三年内把这些知识掌握并巩固的。

故事就先讲到这里，接下来是实证理论。

以下内容摘自 @Thoughts Memo 汉化组的译文《第十八章间隔重复（分散练习）》

学习理论

| 间隔效应

学习新知识只是解决学习难题的一半。另一半挑战在于如何牢记所学内容。要想记住知识，必须定期复习——否则，知识终将被遗忘。

一种常用的可视化记忆遗忘过程的方法是通过遗忘曲线来展示，这一概念最早由 19 世纪末的心理学家赫尔曼·艾宾浩斯提出并研究：

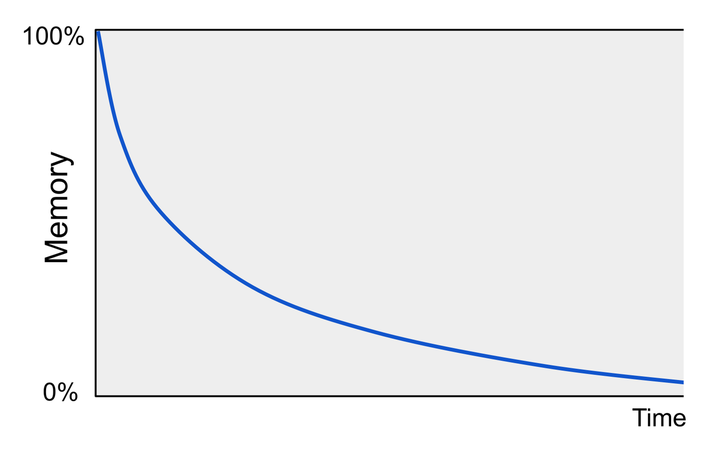
艾宾浩斯（1885）发现，当复习被间隔开来或分散到多个时间中进行（而不是集中在单一时期内）时，不仅能恢复记忆，还能将其进一步巩固到长期记忆中，从而减缓遗忘速度。这种现象现在被称为间隔效应。

| 间隔重复

间隔效应带来的一个深远影响是：完成的复习次数越多（在适当的间隔下），记忆保留的时间就越长，下一次需要复习前的等待时间也就越长。这一发现催生了一种系统复习先前学习材料的方法，称为间隔重复（或分散练习）。在这里，「重复」指的是在适当时机成功进行的复习。

下面是一个例子，用来说明间隔重复的过程和威力。假设你学习了一个新单词。起初，你可能只能记住这个单词一天。但如果你在第二天测试自己对其含义的记忆，那么你可能会记住它直到周末。如果你在周末再次进行自测，那么你可能会记住几周。如果你坚持这种间隔重复的计划，最终你将能够在两次重复之间间隔多年（Bahrick et al., 1993）。

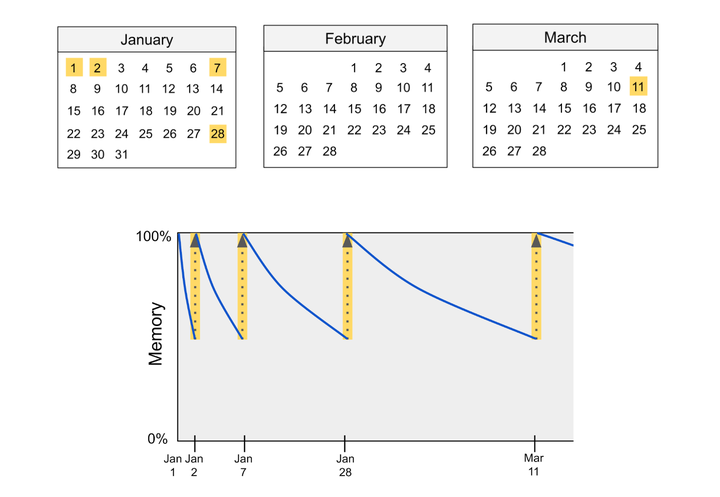
间隔重复的主要挑战在于如何选择最佳的复习间隔时间。如果间隔时间过长，你可能会遗忘所学的内容，导致你在间隔重复安排中倒退。但如果下一次复习来得过早，你的记忆强度就不会得到充分的提升，学习进度也会相应放缓。

| 直观理解间隔重复

Qadir & Imran (2018) 通过类比肌肉锻炼来解释间隔重复，帮助我们直观地理解这一概念：

⠀⠀⠀「……集中学习可能会带来暂时的熟练感，就像健身者通过密集训练可以使肌肉短时间内膨胀起来。然而，只有通过间隔锻炼，肌肉才能真正成长（即锻炼和休息交替进行）。同样，要实现长期有效的学习，也需要采用间隔练习的方，而不是依赖于突击学习。」

Brown, Roediger, & McDaniel (2014, pp.9-10, 81-82, 100-101) 对此进行了深入阐述：

⠀⠀⠀「教育工作者普遍认为，掌握新技能的最有效方法是专注且持续地练习，直到完全掌握为止。这种观念根深蒂固，因为在集中练习的过程中，我们常常能看到快速进步。然而，研究表明，这种集中练习带来的进步往往是短暂的，很快就会消退。

⠀⠀⠀……

⠀⠀⠀集中练习之所以能给我们带来掌握的感觉，是因为我们在短期记忆中不断循环信息，而不需要从长期记忆中重构学习内容。但这种方法，就像反复阅读作为学习策略一样，获得的熟练感是暂时的，掌握感也是虚假的。真正触发知识重新巩固和深度学习的，是那个费力重构知识的过程。

⠀⠀⠀……

⠀⠀⠀当你从短期记忆中回忆所学内容时，比如在快速反复练习中，几乎不需要多少脑力，这样带来的长期收益也很有限。但当你在一段时间后回忆，而对内容的掌握已经有些生疏时，你就必须努力重构它。这种费力的回忆不仅强化了记忆，还能让所学内容重新变得灵活，从而促进了重新巩固。重新巩固有助于用新信息更新记忆，并将其与近期学习的内容联系起来。」

重新巩固的过程可以类比为（第 73-74 页）多次修改一篇文章的过程：

⠀⠀⠀「大脑巩固新知识的过程，可以用写作文章的经历来形象地类比。初稿常常是粗糙而不精确的。你是在写作的过程中逐渐明确自己想表达的内容。经过几轮修改，你的文章会变得更加凝练，多余的内容也会被删除。然后你会暂时搁置文章，让思想沉淀。当你一两天后重新审视时，你要表达的内容在脑中会变得更加清晰。这时你可能会发现自己实际上在阐述三个主要观点。你会将这些观点与读者熟悉的例子和佐证材料联系起来。你会重新组织和整合论点的各个要素，使文章更加有力且优雅。

⠀⠀⠀学习新知识的过程也是如此，开始时常常感觉杂乱无章、难以掌握；最关键的内容并不总是一目了然。知识的巩固有助于组织和固化学习内容。值得注意的是，在一段时间后进行复习也能达到类似的效果。这是因为从长期记忆中检索信息不仅能够强化记忆痕迹，还能使这些记忆再次变得可塑，从而能够与新近学习的内容建立联系。这个过程被称为重新巩固。这正是[间隔]提取练习能够修改和强化学习的原理。」

| 研究者之间的共识

值得注意的是，间隔效应仍然是一个活跃的研究领域。正如 Hartwig, Rohrer, & Dedrick (2022) 所描述，除了重新巩固之外，可能还有其他因素在起作用。尽管间隔效应背后的具体机制可能仍有争议，但其效果和实用价值已经得到研究者的一致认可：

⠀⠀⠀「研究者们已经提出了多种解释间隔效应的理论（相关综述可参见 Benjamin & Tullis, 2010; Delaney et al., 2010; Dempster, 1989）。根据这些理论，间隔效应可能源于以下几种机制：编码变异性（即在两次学习之间的间隔使得上下文变化，从而提供更丰富的编码）、加工不足（即如果两次学习时间相近，第二次对材料的加工会减弱）、记忆巩固（即第二次学习受益于间隔期间发生的记忆巩固过程）或学习阶段的提取（即间隔促进第二次学习时的主动回忆）。然而，目前还没有一种单一机制能够完全解释所有与间隔效应相关的研究发现，可能需要多种机制的结合才能最好地解释这一效应（Delaney et al., 2010）。

⠀⠀⠀无论具体机制如何，间隔效应的稳定性是毋庸置疑的——它在各种学习材料、实验程序和学习者特征中都有所体现（Dunlosky et al., 2013）。对本研究而言最重要的是，间隔效应已经在众多基于课堂的随机对照研究中得到证实（例如，Seabrook et al., 2005; Sobel et al., 2011；综述见 Dunlosky et al., 2013）。此外，课堂研究还发现间隔效应在数学学习中同样有效（Barzagar Nazari & Ebersbach, 2019; Hopkins et al., 2016; Lyle et al., 2020; Schutte et al., 2015）。简而言之，大量数据表明，采用间隔练习的方法可以提高学生在延迟测试中的数学成绩。……研究文献明确指出，如果要让学生长期保持所学知识，练习应该分散在多个课堂环节中进行（Rawson et al., 2013; Rawson et al., 2018）。」

正如 Rohrer (2009) 所言：

⠀⠀⠀「……间隔效应可以说是学习研究领域中最显著且最稳定的发现之一，它似乎适用于各种学习情境。」

事实上，研究者 Kang (2016) 指出，数百项研究已经证实，间隔重复能够产生更优越的长期记忆效果。为了生动说明这一点，他描述了一项最早的间隔重复研究，其结果在过去一个世纪中被 254 项后续研究所反复验证：

⠀⠀⠀「以一项早期研究为例，研究者要求大学生学习雅典誓言 (Gordon, 1925)。他们将学生分为两组：一组连续听 6 次誓言朗读；另一组在第一天听 3 次，三天后再听 3 次。

⠀⠀⠀在即时测试中，集中学习组的表现略优于间隔学习组。然而，在 4 周后的延迟测试中，间隔学习组的表现明显优于集中学习组。

⠀⠀⠀这一结果表明，尽管集中练习在短期内可能看似[略微]更有效，但间隔练习才能产生持久的长期学习效果。」

间隔学习的效果如此显著和确凿，以至于它引起了广告领域的高度关注。在这一领域中，众多研究已经复现了间隔效应在增强消费者对品牌记忆方面的有效性 (Schmidt & Eisend, 2015)。

实证研究

测试效应

以下内容摘自 @Thoughts Memo 汉化组的译文《(2/5) 高效学习的间隔重复——文献综述之测试效应》

测试效应是广受承认的心理学现象，表明了单纯测试记忆的行为就会增强记忆（无论是否有反馈）。既然间隔重复的本质就是在特定的日子进行测试，我们便能得出测试比普通复习或者学习有更好的效果，而且不仅适用于记忆随便一个日期。下列是一些有关论文：

Allen, G.A., Mahler, W.A., & Estes, W.K. (1969). “Effects of recall tests on long-term retention of paired associates”⁠. Journal of Verbal Learning and Verbal Behavior, 8, 463-470

进行一次测试，一天之后的记忆强度相当于学习 5 次；与集中回顾相比，间隔可以提高保留率。
Karpicke & Roediger (2003). “The Critical Importance of Retrieval for Learning”

学习斯瓦希里语词汇的实验中，学生遵循不同的流程，有的接受测试，有的学习，有的两者都做；学习阶段各组得分相似。研究人员要求学生预测他们能记住的词汇所占比重（所有小组的预测的平均值是 50%）。一周后，接受测试的学生记住了大约 80% 的词汇，而没有测试的学生记住了大约 35%。一些学生测试或学习的时长比其他学生更久，然而一旦记忆成型了，收益递减便如影随形。学生们报告说，他们很少测试自己，也很少测试已经学过的内容。

总结：同样，与学习相比，测试可以改善记忆。而且，没有学生知道这一点。
Roediger & Karpicke (2006a). “Test-Enhanced Learning: Taking Memory Tests Improves Long-Term Retention”

学生在读完文章 5 分钟、2 天、1 周后就文章阅读理解接受考查（没有反馈）。5 分钟之后考查，学习材料完胜测试，但其他时刻后就不一样了；然而学生认为，无论何时接受考查，学习都胜过测试一筹。1 周之后，测试成绩为 60%，而学习为 40%。

总结：与学习相比，测试更能改善记忆。所有人（老师&学生）“觉得”恰好相反。
Karpicke & Roediger (2006a). “Expanding retrieval promotes short-term retention, but equal interval retrieval enhances long-term retention”

一般科学散文理解；摘自 Roediger & Karpicke 2006b：「两天后，初次测试比重复学习的记忆效果更好 (68% 比 54%)，一周后再观察，测试比重复学习仍有优势 (56% 比 42%)。」
Roediger & Karpicke (2006b). “The Power of Testing Memory: Basic Research and Implications for Educational Practice”

文献综述：有 7 项1941 年之前的研究证明测试可以提高保留率，而在 1941 年之后的研究也有 6 项。另见综述 “Spacing Learning Events Over Time: What the Research Says” & “Using spacing to enhance diverse forms of learning: Review of recent research and implications for instruction”⁠, Carpenter et al 2012。
Agarwal et al 2008, “Examining the Testing Effect with Open- and Closed-Book Tests”

与 #2 一样，从长远来看，更纯粹的测试形式（也就是开卷测试而非闭卷测试）表现得更好，学生对于哪种测试更有效果上是受蒙蔽的。
Bangert-Drowns et al 1991. “Effects of frequent classroom testing”

有 35 项研究在学期中展开各式测试。对这些研究进行元分析，发现 29 例发现测试有好处；5 例发现有坏处；1 例结果为无效果。元分析发现，即使只测试一次，也会带来巨大的好处，之后回报就会递减。
Cook 2006, “Impact of self-assessment questions and learning styles in Web-based learning: a randomized, controlled, crossover trial”⁠；医生（住院医师）带着问题学习的话，最终得分更高。
Johnson & Kiviniemi 2009, “The Effect of Online Chapter Quizzes on Exam Performance in an Undergraduate Social Psychology Course”（「这项研究考察了基于掌握学习理论的每周强制阅读测验对于提高考试和课程表现的有效程度。能完成阅读测验与更好的考试和课程表现有关。」)；另见 McDaniel et al 2012⁠。
Metsämuuronen 2013, “Effect of Repeated Testing on the Development of Secondary Language Proficiency”
Meyer & Logan 2013, “Taking the Testing Effect Beyond the College Freshman: Benefits for Lifelong Learning”⁠; 证实测试效应在老年人中与年轻人有相近的效应量
Larsen & Butler 2013, “Test-enhanced learning”
Yang et al 2021, “Testing (Quizzing) Boosts Classroom Learning: A Systematic And Meta–Analytic Review”

间隔效应

以下内容摘自 @Thoughts Memo 汉化组的译文《(3/5) 高效学习的间隔重复——文献综述之间隔效应》

测试的时机至关重要。上文中，我们注意到学完知识之后测试是有些好处，但是同样数量的测试分散到不同时机进行，更能实现间隔效应或者间隔重复。有上百个研究涉及间隔效应：

Cepeda et al 2006 这篇综述对 184 篇文章共计 317 个实验做了总结；其他综述包括：
Ruch 1928, “Factors influencing the relative economy of massed and distributed practice in learning”
Crowder 1976, Principles of learning and memory
Dempster 1989, “Spacing effects and their implications for theory and practice”
Delaney et al 2010, “Spacing and testing effects: A deeply critical, lengthy, and at times discursive review of the literature”
Donovan & Radosevich 1999, “A meta-analytic review of the distribution of practice effect: Now you see it, now you don’t”
Greene 1992, Human memory: Paradigms and paradoxes
Janiszewski et al 2003, “A meta-analysis of the spacing effect in verbal learning: Implications for research on advertising repetition and consumer memory”
Pavlik & Anderson 2003, “An ACT-R model of the spacing effect”
Balota et al 2006, “Is Expanded Retrieval Practice a Superior Form of Spaced Retrieval? A Critical Review of the Extant Literature”
Carpenter et al 2012, “Using Spacing to Enhance Diverse Forms of Learning: Review of Recent Research and Implications for Instruction”

他们几乎一致地发现，若最终测试/测量在几天或几年后进行的话，间隔测试优于集中测试[30]⁠，尽管其中机制并未知晓[31⁠]。除了前面提到的研究外，我们还有：

Peterson, L. R., Wampler, R., Kirkpatrick, M., & Saltzman, D. (1963). “Effect of spacing presentations on retention of a paired associate over short intervals”⁠. Journal of Experimental Psychology, 66(2), 206-209
Glenberg, A. M. (1977). “Influences of retrieval processes on the spacing effect in free recall”⁠. Journal of Experimental Psychology: Human Learning and Memory, 3(3), 282-294
Balota et al 1989, “Age-related differences in the impact of spacing, lag and retention interval”⁠. Psychology and Aging, 4, 3-9

大量研究文献都在探究“什么样”的间隔安排是最好的，以及如此安排所反映出的记忆性质：是间隔固定不动好，还是间隔逐渐变大好？这对于理解记忆以及建立记忆模型都非常重要，同时也有助于将间隔重复融入课堂（比如Kelley & Whatson 2013年研究使用的安排是10分钟学习/10分钟休息，将同样材料重复三次，其意图是促使材料进入长期记忆？）但是对于实践来说，这个研究方向不是很有趣：总的来说，很多研究众说纷纭，但给出的安排效率虽有差异，也不算显著。大多数现存材料都模仿 Supermemo, 使用了间隔变大的算法，所以没什么好担心的； Mnemosyne 的开发者 Peter Bienstman 说，尚不清楚更复杂的算法能否有助益[32]⁠, Anki 开发者担心重新实现 Supermemo 的专有算法太难也太复杂，却看不到显著成效，同时 SM3+ 算法为了极尽优化可能造成更多错误。所以他们也有同感。

如果有人感兴趣，有 3 项研究发现固定间隔比递增间隔更好：

Carpenter, S. K., & DeLosh, E. L. (2005). “Application of the testing and spacing effects to name learning”⁠. Applied Cognitive Psychology, 19, 619-636[33]
Logan, J. M. (2004). Spaced and expanded retrieval effects in younger and older adults. Unpublished doctoral dissertation, Washington University, St. Louis, MO

这篇论文很有趣，因为洛根发现，一天之后测试，使用递增间隔复习的年轻人表现要差得多。
Karpicke & Roediger, 2006a

撇开固定间隔的问题与递增间隔的问题不谈，有更多通用研究指出间隔学习相对集中学习的好处，见下面的列表：

Cepeda et al 2006 （大综述，本页中其他地方用到）
Karpicke & Roediger 2006a
Rohrer & Taylor 2006. “The effects of over-learning and distributed practice on the retention of mathematics knowledge”⁠. Applied Cognitive Psychology, 20: 1209-1224 (参见 Rohrer & Taylor 2007⁠, Rohrer et al 2005)
Seabrook et al 2005. “Distributed and Massed Practice: From Laboratory to Classroom”
Keppel, Geoffrey. “A Reconsideration of the Extinction-Recovery Theory”⁠. Journal of Verbal Learning & Verbal Behavior. 6(4) 1967, 476-486

一周后，集中复习者从 5.9 正确 → 2.1；间隔复习者从 5.5 → 5.0。(请注意，通常的观察是集中学习最初更好，后来变得更差，正确率是最初的一半不到)
Bloom & Schuell 1981, “Effects of massed and distributed practice on the learning and retention of second-language vocabulary”

在两个高中组记住 16 个法语单词四天后，间隔组还记得 15 个，集中组还记得 11 个。
Rea, Cornelius P; Modigliani, Vito. “The effect of expanded versus massed practice on the retention of multiplication facts and spelling lists”⁠. Human Learning: Journal of Practical Research & Applications. Vol 4(1) Jan-Mar 1985, 11-18[34]

培训后立即进行测试，结果间隔组（70% 正确）比集中组（53% 正确）表现更好。这些结果似乎表明，间隔效应适用于学龄儿童，至少适用于学校通常教授的一些材料。[35]

Donovan & Radosevich 1999, “A meta-analytic review of the distribution of practice effect: Now you see it, now you don’t”:

根据多诺万和拉多塞维奇对间隔学习研究的元分析，间隔效应的效应量为 d = 0.42. 这意味着接受间隔练习后的平均记忆效果，优于约 67% 集中练习者的记忆效果。这个效应量不容小觑——在教育研究中，即使效应量低到 d = 0.2 都认为是“足够显著”，而高于 d = 1 的效应量则少之又少。[36]

例如，在 Donovan 和 Radosevich (1999) 的一项元分析中，随着任务的概念难度从低（如旋转追视）到平均（例如单词列表回忆）再到高（例如拼图），间隔效应的效应量急剧减少。根据这一发现，对于许多数学任务来说，间隔练习的好处可能会变得微不足道。[37]

（注：旋转追视是用于测试手眼协调和运动技能学习的测试，受试者需要用指示物追踪旋转圆盘上的圆点）

Donovan 的元分析指出，在使用更好方法的研究中，效应量虽然变小，但仍然不容小觑。

Bahrick, Harry P; Phelphs, Elizabeth. “Retention of Spanish vocabulary over 8 years”⁠. Journal of Experimental Psychology: Learning, Memory, & Cognition. Vol 13(2) April 1987, 344-349; 这篇研究初始训练之后的间隔特别长，很有意思

Harry Bahrick 和 Elizabeth Phelps (1987) 研究了 50 个西班牙语词汇在 8 年之后的保留情况。受试者被分成三组。每个人练习七到八次，间隔几分钟，1 天或 30 天。在每个环节中，受试者都会进行练习，直到他们可以一次性完美回忆出单词列表…8 年后，无延迟组的人能记住 6% 的单词，延迟 1 天组的人能记住 8% ，30 天组的人平均能记住 15%。每个人都参加了选择题测试，其中再次观察到了间隔效应。无延迟组得分为 71%，一天组得分为 80%，30 天组得分为 83%。

…Bahrick 和他的同事们改变了练习的间隔和练习量。练习环节之间有间隔 14 天、28 天或 56 天的，总共进行 13 或 26 次练习。他们测试了受试者在训练后一年、二年、三年和五年的记忆。有一次观察到，当练习环节间隔较长时，在每个练习环节中达到标准所需的时间稍长一些，但同样，这一小投资在几年后产生了回报。测试是在练习后一年、两年、三年还是五年进行的并不重要——56 天组总是记住最多的，28 天组次之，14 天组记忆最少。而且影响是比较大的。如果每 14 天练习一次单词，你需要的练习次数是每 56 天练习一次时的两倍，才能达到同样的表现水平！

Pashler et al, 2003; “Is Temporal Spacing of Tests Helpful Even When It Inflates Error Rates?”

测试之间的长间隔必然意味着你经常会回答错误；有人认为答错就会削弱学习效果。尽管短期内过多的错误的确会降低准确性，但长间隔的力量足以让他们仍然获胜。
间隔重复在患病人群中的研究：

让阿尔茨海默病患者进行短期复习的研究；间隔时间以秒和分钟为单位，在物体位置教学或日常任务方面取得了一定成功 38:

Camp, C. J. (1989). “Facilitation of new learning in Alzheimer’s disease”. In G. C. Gilmore, P. J. Whitehouse, & M. L. Wykle (Eds.), Memory, aging, and dementia (pp. 212-225)
Camp, C. J., & McKitrick, L. A. (1992). “Memory interventions in Alzheimer’s-type dementia populations: Methodological and theoretical issues”. In R. L. West & J. D. Sinnott (Eds.), Everyday memory and aging: Current research and methodology (pp. 152-172) -

针对创伤性脑损伤患者的研究; Goverover et al 2009, “Application of the spacing effect to improve learning and memory for functional tasks in traumatic brain injury: a pilot study”
和多发性硬化症患者的研究; Goverover et al 2009, “A functional application of the spacing effect to improve learning and memory in persons with multiple sclerosis”

数学[39]:

乘法 (Ria & Modigliani 1985)
遍历数列排列 (Rohrer & Taylor 2006)on
计算多面体体积 (Rohrer & Taylor 2007)
统计 (Smith & Rothkopf 1984)

初级微积分 (Revak 1997[40] 但也有一篇相关文章说明对微积分 I 无效) 和代数 (Mayfield & Chase 2002⁠, Patac & Patac 2013⁠; 可能没效果, Sutherland 2013)
医学 (Kerfoot & Brotschi 2009⁠, Shaw et al 2012⁠; Kerfoot 2009⁠, 是 Kerfoot et al 2007 两年后的跟进研究。Kerfoot 有其他一些相关研究⁠; Gyorki et al 2013) ；在手术方面 (Moulton et al 2006, “Teaching Surgical Skills: What Kind of Practice Makes Perfect? A Randomized, Controlled Trial”⁠, 微血管缝合的间隔重复实践；Spruit et al 2014)
心理学导论 (Balch 2006, “Encouraging Distributed Study: A Classroom Experiment on the Spacing Effect”[41⁠]. Teaching of Psychology, 33, 249-252)
8 年级美国历史 (Carpenter, Pashler, and Cepeda 2009)
用自然拼读法学习阅读 (Seabrook et al 2005)
音乐 (Stambaugh 2009)
生物 (中学生物；Kelly&Whatson 2013)
统计 (初步内容；Maas 等人于2015年)
记忆网站密码 (Bonneau & Schechter 2014⁠, Blocki et al 2014⁠, Blum & Vempala 2017)
可能不是澳大利亚宪法 (Colbran et al 2015 年)

数学建模

这里我直接引用全球最顶级的记忆算法团队的论文。

以下内容摘自 @墨墨背单词的算法研究《优化间隔重复调度的随机最短路径算法 | 墨墨百科》和《通过捕捉记忆动态，优化间隔重复调度 | 墨墨百科》

2 时间序列记忆模型

2.1 时序数据

学习者的一个最小记忆行为事件可以用一个四元组来表示：

$e :=(u, w, \Delta t, r)$

其中：

$u$ 表示学习者
$w$ 表示要记忆的单词
$\Delta t$ 表示自上次复习以来的时间间隔
$r$ 表示学习者是否成功地回忆起该单词

为了得到时序数据，我们将学习者对同一单词的所有记忆行为按照发生时间排序，然后将 $\Delta t$ 和 $r$ 按顺序拼接，得到一个序列特征

$e_{i} :=(u, w, \boldsymbol{\Delta t}_{1:i-1}, \boldsymbol r_{1:i-1} , \Delta t_{i} , r_{i})$

其中

$\boldsymbol{\Delta t}_{1:i-1}$ 表示第 $i$ 次复习之前每次复习之间的时间间隔
$\boldsymbol r_{1:i-1}$ 表示第 $i$ 次复习之前每次复习的反馈情况

样例请见表 1：

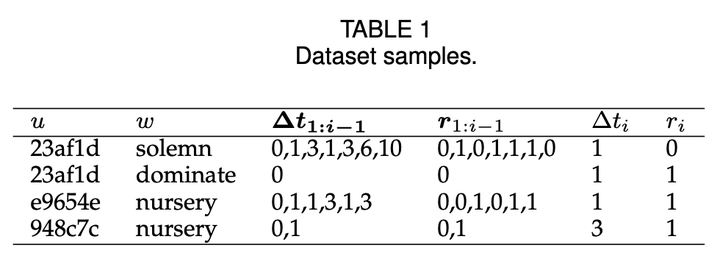
然而，处理后的数据中，回忆依然是二元，由于记忆内在的不确定性，回忆的结果服从一个概率随着时间变化的 0-1 分布。我们更关心学习者记忆内在的回忆概率及其变化，因此需要对上述数据进一步处理。

最容易想到的处理方法是按照 $w, \boldsymbol{\Delta t}_{1:i-1}, \boldsymbol r_{1:i-1}, \Delta t_{i}$ 分组，计算 $r_i$ 的均值，即可估计不同单词在不同记忆行为历史下的回忆概率：

$e_{i} :=(w, \boldsymbol{\Delta t}_{1:i-1}, \boldsymbol r_{1:i-1}, \Delta t_{i} , p_{i}, N)$

这种处理方法忽略了学习者本身的特质。但即使如此，由于时序数据的空间维度随着序列长度指数爆炸，我们收集到的数据在进行分组后，每组的样本量较少，估计误差较大。为了缓解数据稀疏性，降低误差的方差，我们将单词划分为了 10 个难度，如图 2 和表 2 所示：

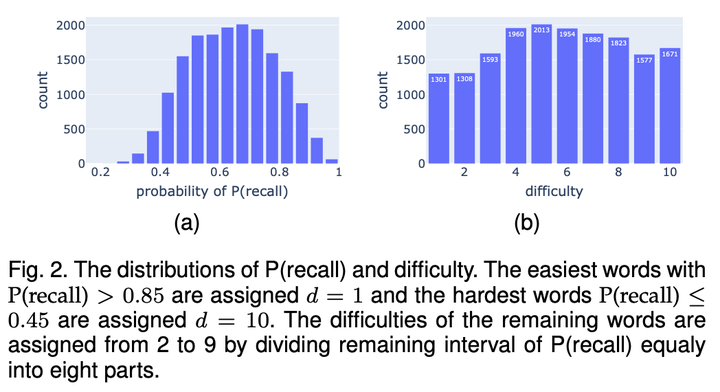
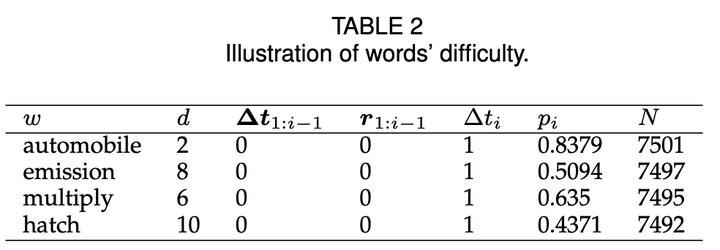
然后按照单词难度、记忆行为历史进行分组，得到每组的回忆概率和分组样本量。然后采用指数遗忘曲线回归，计算每个分组的记忆半衰期。

$e_{i} :=(d, \boldsymbol{\Delta t}_{1:i-1}, \boldsymbol r_{1:i-1}, \boldsymbol p_{1:i-1}, \Delta t_{i} , p_{i}, h_{i-1}, N)$

样例请见表 3：

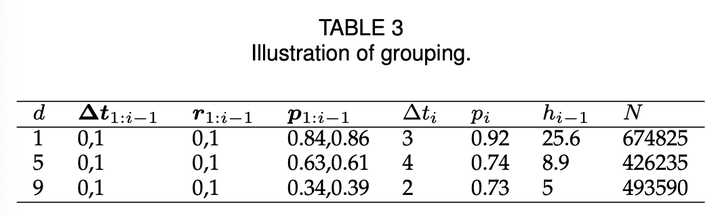
2.2 半衰期回归模型 HLR

半衰期指的是回忆概率从 100% 下降到 50% 所需到时间。

$p = 2^{-\Delta/h}$

在半衰期回归模型中，半衰期的观测值是通过上述公式拟合得到的。

Duolingo 的论文采用统计特征来预测半衰期：

$\begin{aligned}\hat{h}_{\boldsymbol\Theta} & =2^{\boldsymbol\Theta \cdot \boldsymbol x}\\\boldsymbol x & = (x_{\oplus},x_{\ominus}, \boldsymbol{lex}),\end{aligned}$

我们在该模型的基础上，引入了时间序列信息，并使用两种时序模型进行预测。

2.3 DHP-HLR 模型

在第一个记忆模型中，我们主要考虑简单性和可解释性，为此我们手工搭建了一个满足马尔可夫性的时序模型。

马尔可夫性：当前状态只取决于上一个状态

在这个模型中，我们将时间序列降维成状态变量和状态转换方程。我们考虑以下四个状态变量：

半衰期：其衡量了记忆的存储强度
回忆概率：其衡量了记忆的提取强度
回忆结果：记住 or 忘记
难度：在同等条件下，半衰期增长越慢，记忆巩固的难度越高

在我们构建时序数据时，每个时间序列已经标记上了这四个状态变量。将时间序列数据投影到三维空间后，得到了图 3：

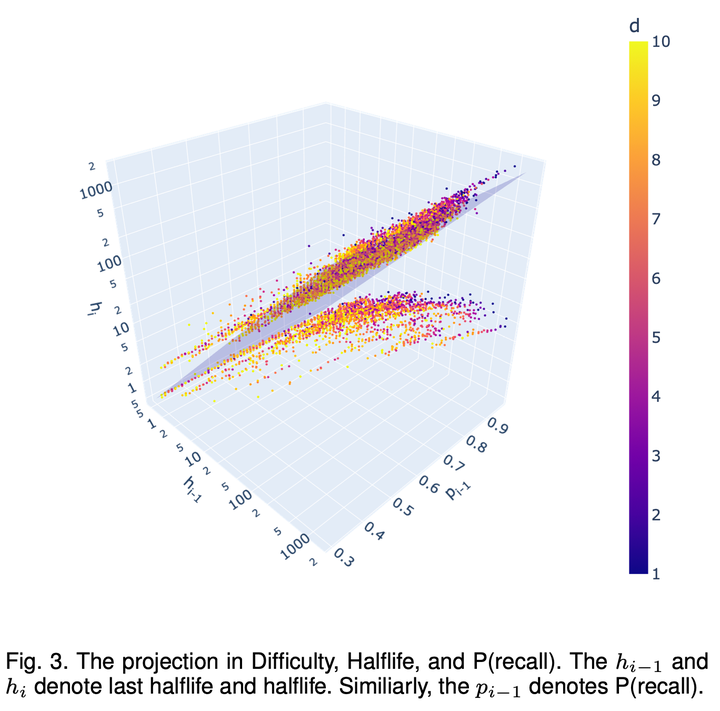
X 轴表示复习前的保留率 $p_{i-1}$ ， Y 轴表示复习前的记忆半衰期 $h_{i-1}$ ， Z 轴表示复习后的记忆半衰期 $h_i$ ，颜色表示单词的难度，而中间的淡紫色平面分隔开了复习结果为记住和忘记的两类样本。

通过观察图 3，我们发现当回忆结果为记住时，复习后的记忆半衰期会比复习前的长。而当回忆结果为遗忘时，记忆半衰期会缩短。

为了更细致地研究复习对记忆半衰期的影响，特别是复习时回忆概率对记忆半衰期的影响，我们选择了一组复习前后的数据，计算记忆半衰期，绘制遗忘曲线，得到图 4：

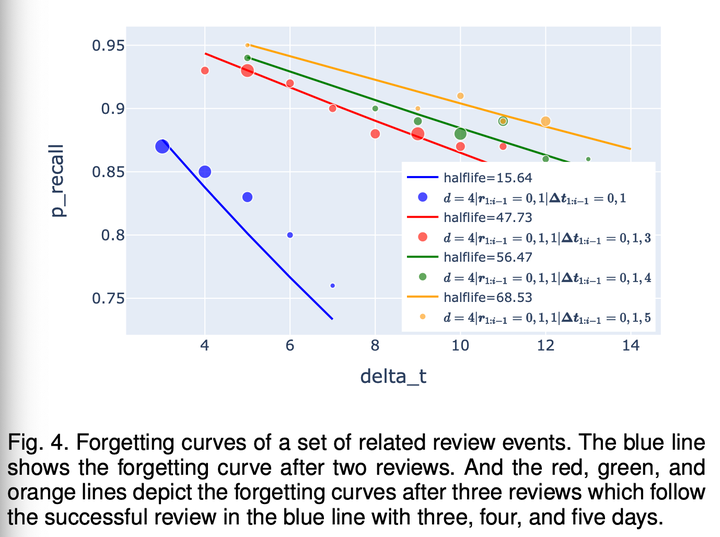
图：一组相关复习事件的遗忘曲线。蓝色的遗忘曲线展示了两次复习后，在不同间隔下进行第三次复习的回忆概率。红、绿、黄三条曲线是分别隔 3 天、4 天、5 天的第三次复习回忆成功后的遗忘曲线。

根据图 4 可知，随着复习间隔增长，回忆成功后的记忆半衰期也在增长。而根据遗忘曲线的规律，复习间隔增长会导致回忆概率下降。因此当回忆概率下降时，回忆成功的记忆半衰期会增长。

考虑以上观察结果，我们对记忆半衰期和难度分别构建了状态转移方程：

$h_i =[h_{i-1} \cdot (e^{\boldsymbol \theta_1 \cdot \boldsymbol x_{i-1}}+1),e^{\boldsymbol \theta_2 \cdot \boldsymbol x_{i-1}}] \cdot [r_{i-1}, 1-r_{i-1}]^T$

其中 $\boldsymbol x_i = [\log d_{i-1}, \log h_{i-1},\log(1-p_i)]$ 是特征向量，包含了难度、半衰期和回忆概率。

$d_i = [d_{i-1}, d_{i-1} + \theta_3]\cdot[r_{i-1}, 1-r_{i-1}]^T$

在记住时，难度不发生变化，在遗忘时，难度增加。

最终的状态转移方程组为：

$\begin{aligned}\left[\begin{array}{c} h_i \\ d_i \end{array}\right] & =\left[\begin{array}{cc} h_{i-1} \left(e^{\boldsymbol{\theta}_{1} \cdot \boldsymbol{x}_{i-1}}+1\right) & e^{\boldsymbol{\theta}_{2} \cdot \boldsymbol{x}_{i-1}} \\ d_{i-1} & d_{i-1}+\theta_{3} \end{array}\right]\left[\begin{array}{c} r_{i-1} \\ 1-r_{i-1} \end{array}\right] \\\boldsymbol x_{i-1}& = [\log d_{i-1}, \log h_{i-1},\log(1-p_{i-1})] \\r_{i-1}& \sim Bernoulli(p_{i-1})\\p_{i-1}& =2^{-\Delta t_{i-1}/h_{i-1}} \\h_1& = - 1 / \log_2(0.925 - 0.05 \cdot d_0),\end{aligned}$

基于上述方程，给定初始难度和半衰期，我们就可以计算任何记忆行为序列对应的记忆状态。

图 5 更清晰地描述了计算过程中，每个变量之间的关系。

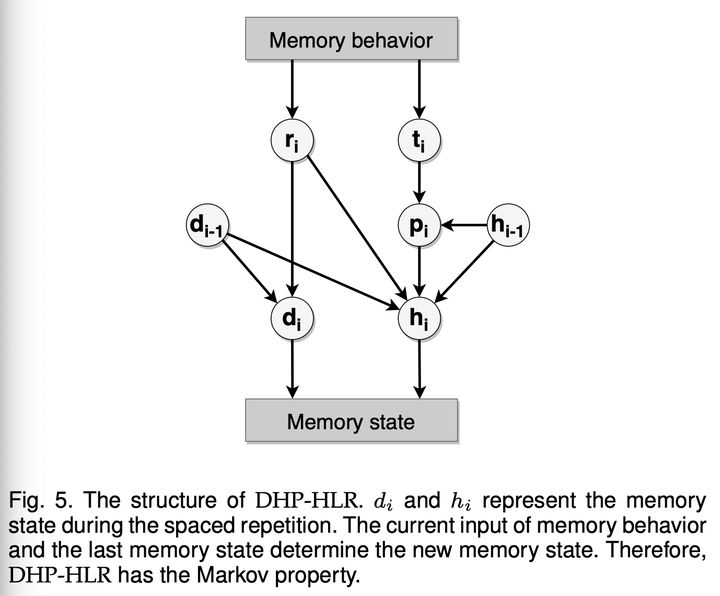
2.4 GRU-HLR 模型

DHP-HLR 为了可解释性，要求人工设计状态转移方程，牺牲了一部分预测能力。而循环神经网络是预测时序任务的常见方法，GRU 门控神经网络是一个具有代表性的循环神经网络。通过引入 GRU，我们可以无需人工设计状态转移方程。

$\hat{h}_i=\mathrm{GRU}(\boldsymbol{\Delta t}_{1:i-1}, \boldsymbol r_{1:i-1}, \boldsymbol p_{1:i-1})$

为了降低回忆概率的预测误差，我们设计了如下的损失函数：

$l(e_{i},\boldsymbol\theta)=|\frac{h_{i}-\hat{h}_{i}}{h_{i}+\hat{h}_{i}}|+C||\boldsymbol\theta||_{2}^{2}$

这里我们采用了对称平均绝对百分比误差，可以降低预测半衰期的百分比误差，从而降低对回忆概率对绝对误差。

同时，GRU-HLR 不仅可以用于预测半衰期和回忆概率，还可以捕捉记忆的动态。只需要将隐藏层输出作为记忆状态

$\boldsymbol h_{i}, \boldsymbol s_{i}=\textrm{GRU-HLR}(\boldsymbol s_{i-1}, \Delta t_{i-1}, r_{i-1}, p_{i-1})$

其中 s 对应了单词在学习者大脑中的记忆状态。GRU-HLR 描述了记忆状态在复习前后发生的变化。

3 间隔重复调度优化

3.1 问题设置

间隔重复方法的目的在于帮助学习者高效地形成长期记忆。而记忆半衰期反映了长期记忆的存储强度，复习次数、每次复习所花费的时间则反映了记忆的成本。所以，间隔重复调度优化的目标可以表述为：在给定记忆成本约束内，尽可能让更多的材料达到目标半衰期，或以最小的记忆成本让一定量的记忆材料达到目标半衰期。其中，后者的问题可以简化为如何以最小的记忆成本让一条记忆材料达到目标半衰期，即最小化记忆成本（Minimize Memorization Cost，MMC）。

我们所构建的长期记忆模型满足马尔可夫性，在 DHP-HLR 和 GRU-HLR 中，每个记忆状态仅依赖于上一个状态、当前的复习间隔和回忆结果，回忆结果的分布依赖于复习间隔。其中回忆结果服从一个与复习间隔有关的随机分布。由于半衰期状态转移存在随机性，一条记忆材料达到目标半衰期所需的复习次数是不确定的。因此，间隔重复调度问题可以视作一个无限时间的随机动态规划问题。考虑到优化目标是让记忆半衰期达到目标水平，所以本问题存在终止状态，所以可以转化为一个随机最短路径问题（Stochastic Shortest Path，SSP）。结合优化目标，我们将算法命名为 SSP-MMC。

随机最短路径问题（Stochastic Shortest Path problem，SSP）是一种马尔可夫决策过程（Markov Decision Process，MDP），它是对经典的确定性最短路径问题的一般化。我们的目标是控制一个动态演化的系统中的智能体，让它收敛到一个预先定义的目标。智能体通过在每个时间段内采取行动来进行控制：这些行动都会产生一定的代价，而系统中的转移则由只与上一次行动有关的概率分布来控制，与过去无关。我们的重点是有限的状态/行动空间：即在给定初始状态的情况下，选择每个状态的行动，即确定性的、固定的策略，以使智能体在到达目标状态之前所承担的总期望代价最小化。

结合优化目标，我们将算法命名为 SSP-MMC。

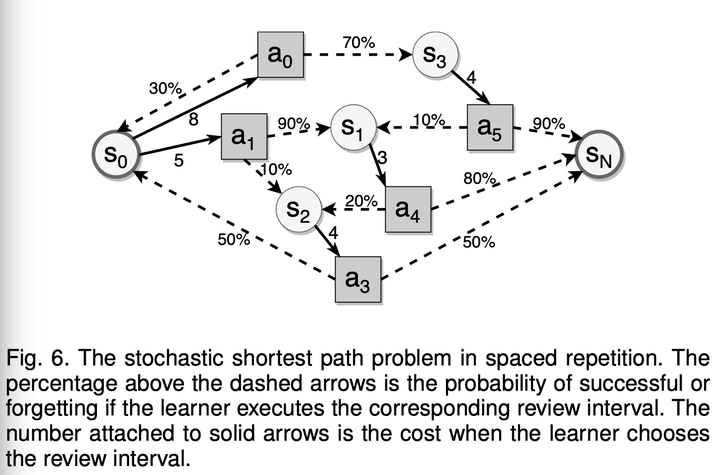
如图 6 所示，圆形表示记忆状态，正方形表示复习行为（即本次复习后的间隔），虚线箭头代表给定复习间隔后的记忆状态转移方向，实线箭头代表给定记忆状态下可选的复习间隔。间隔重复中的随机最短路径问题，就是从初始记忆状态出发，找到每个记忆状态下最优的复习间隔，最小化达到目标记忆状态所需的期望复习成本。

3.2 数学表示

为了解决这个问题，我们提出的方法是将一个单词的复习过程建模为一个 MDP（马尔可夫决策过程），有一组状态 $\mathcal{S}$ 、行动 $\mathcal{A}$ 、状态转换概率 $\mathcal{P}$ 、成本函数 $\mathcal{J}$ 。智能体的目标是找到一个策略 $\pi$ ，使达到目标状态 $s_N$ 的期望成本最小。

$\pi^{*}=\underset{\pi \in \Pi}{\operatorname{argmin}} \lim\limits_{N\to \infty} \mathbb{E}_{s_{0}, a_{0}, \ldots}\left[\sum_{t=0}^{N} \mathcal{J}\left(s_{t}, a_{t}\right) \mid \pi\right]$

状态空间 $\mathcal{S}$ 取决于记忆模型的状态大小。DHP-HLR 模型只有两个状态变量，因此状态可以表述为 $s=(d, h)$ 。对于 GRU-HLR 模型，状态依赖于隐藏层的大小，其使用 $\tanh$ 作为激活函数，其范围为 (-1,1)。它可以被离散化，如下所示：

$S\xrightarrow[]{(\lfloor\frac{s}{\varepsilon}\rfloor|s\in \mathcal{S})}\mathrm{S}$

其中 $\varepsilon$ 是离散化的精度。

行为空间 $\mathcal{A}=\{\Delta t_1,\Delta t_2,\cdots,\Delta t_n\}$ 由可以安排复习的 n 个间隔组成。状态转移概率 $\mathcal{P}_{s,a}(s')$ 是记忆在状态 $s$ 和行动 $a$ 时转移到状态 $s'$ 的概率。成本函数 $\mathcal{J}$ 定义为：

$\begin{aligned}\mathcal{J}(s_0) & = \lim\limits_{N\to \infty} E\left\{\sum\limits_{t=0}^{N-1}g_t(s_t,a_t(s_t), r_t) \right\} \\r_{t}& \sim Bernoulli(p_{t}),\end{aligned}$

其中 $g_t$ 是单步成本， $r_t$ 是 0-1 分布的回忆结果。目标状态 $s_N$ 对应于大于 $h_N$ 的半衰期，这就是目标半衰期。

3.3 优化算法

我们使用值迭代（VI）来解决 MDP( $\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{J}$ )，并使用 DHP-HLR 和 GRU-HLR 来捕捉记忆状态的动态。其贝尔曼方程为：

$\begin{aligned}\mathcal{J}^*(s) & = \min\limits_{a \in \mathcal{A}(s)} \left\{\sum\limits_{s'}\mathcal{P}_{s,a}(s')(g(r) + \mathcal{J}^*(s'))\right\}\\s' & = \mathcal{F}(s,a,r,p),\end{aligned}$