如何高效地记忆？

利益相关：墨墨记忆算法工程师。

我从最优控制的角度来讨论一下如何高效地记忆。当然，你也可以直接看我的论文：A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling | Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining。

首先，让我们来定义一下什么叫做「高效」：给定时间限制，记住最多内容；或给定记住多少内容，花费最少时间。问题来了，怎么才算记住呢？我今天记一个手机号码，和记我自己名字，显然是不一样的：前者我明天很可能就会忘记，后者我明天很可能还记得。记忆之间存在不同的「寿命」。显然我们平常所说的记住肯定不是短期记住，而是长期记忆。

那么，先让我们定义一下记忆的「寿命」。这里有一个很反直觉的事实：遗忘是随机的。哪怕再有把握记住的知识，如果不进行复习，十年后也很可能会忘记。想想你中考、高考时还能回答的问题，现在还记得多少？

所以，给记忆定义一个明确的「寿命」，在此之前一定记得，在此之后一定遗忘，是做不到的。我们需要引入概率。类比一下同位素衰变的例子：我们无法得知一个原子多久之后会衰变，但我们能知道 1 克某原子组成的物质多久后会衰变一半。记忆也是如此，我们可以用「记忆半衰期」来衡量记忆的「寿命」。具体的例子可以看下图的遗忘曲线，记忆半衰期越长，遗忘曲线就越平缓。

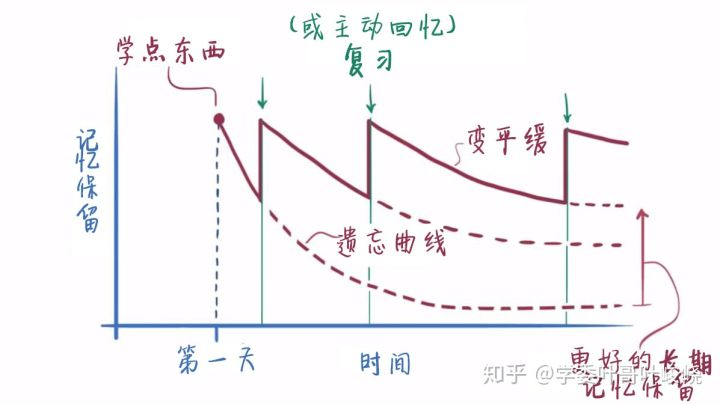
同时，这幅图中还表明了一点：复习会对记忆半衰期产生影响。不断复习，可以让记忆半衰期增长。并且，不同的复习周期对记忆半衰期的影响也是不同的。

回到我们对「高效」的定义，有了记忆半衰期，我们就可以更有意义地定义「高效」：

在给定记忆成本约束内，尽可能让更多的知识达到目标半衰期，或以最小的记忆成本让一定量的知识达到目标半衰期。

其中，记忆成本约束包括时间、精力、情感等等，为了简化问题，我们可以只考虑花在记忆上的时间。而目标半衰期则是我们对记忆的要求，越长的记忆半衰期意味着越牢固的长期记忆。但只要目标半衰期一致，我们就可以对比不同复习方法花费的时间，从而选出最高效的复习方法。

为了进一步简化这个问题，我们考虑在只有一条知识需要记忆的情况：

如何以最小的记忆成本让一条知识达到目标半衰期

在间隔重复中，能够调整的就是每次复习之间的间隔。如何找到最优的复习间隔呢？由于目标半衰期的增长取决于复习时的记忆状态，并且复习的成功与失败也是概率事件，所以我们可以将间隔重复中的记忆半衰期变化用下图表示：

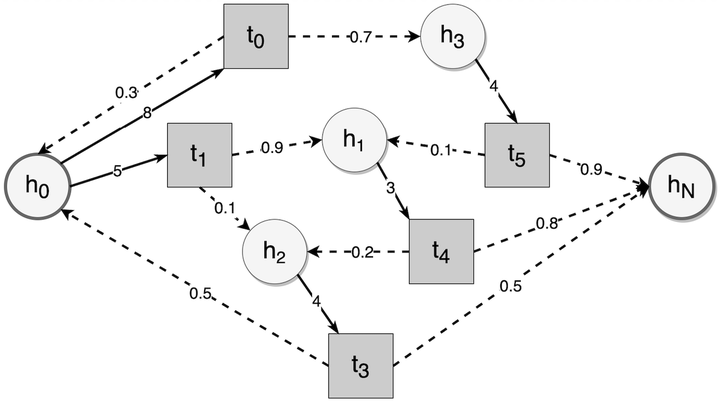
圆圈是半衰期状态，方块是复习间隔，虚线箭头表示给定复习间隔后转移到的半衰期状态，线上的数值表示转移概率，实线箭头指向可选的复习间隔，线上的数值表示复习间隔对应的记忆成本。我们要找到一条从起点到终点最短的路径，以最小化记忆成本，实现高效记忆。该问题就是一个随机最短路径问题，可以用最优控制中的值迭代方法求解。让我们列出贝尔曼方程：

这个方程表示，我们对于每一个记忆状态，都找一个能让期望复习成本最小化的复习间隔。有点类似动态规划，只不过加了期望。然后我们用随机动态规划编程，下面是伪代码：

更详细的介绍可以看我的研究经历和间隔重复算法教程：

是不是看到这里一头雾水，本来想知道怎么高效记忆，现在更糊涂了？没关系，上述建模和公式推导都可以由算法自动完成，如果你想要高效记忆单词，可以用 @墨墨背单词 ，其部署了上述算法。如果你想要记忆别的知识，比如心理学、教育学、社会学等等，可以试试 @Markji APP。当然，如果不想花钱，可以用 Anki（一款开源的间隔重复软件，除了 iOS，其他端都是免费的），教程我也写了很多，请见：

← 返回目录