从一个记忆伪概念，到记忆研究的难题。

引入

读者朋友们，我回来啦！最近整理记忆研究和相关产品，有了一些思考，想要分享给大家。

本来想要系统地介绍一下记忆研究，但是由于内容过于枯燥，还有不少数学公式，大家可能不会喜欢。

所以，本文就从一个常见的记忆「伪概念」说起，把记忆研究的相关内容用一系列问题串起来，方便大家阅读和理解。

废话不多说，让我们开始吧！

伪概念：遗忘临界点是记忆与遗忘明确边界？

遗忘临界点这个词，经常在所谓的「艾宾浩斯遗忘曲线^[1]」相关的记忆方法中出现。但是遗忘临界点的具体内涵是什么？那些兜售相关概念的「记忆砖家」大概会说，这是遗忘快要发生的时刻。

显然，这种解释是站不住脚的。因为，遗忘从记忆后的一刻就开始了。并不存在一个临界点，在此之前都记住，在此之后都遗忘。（不然遗忘曲线怎么会是连续的）

当然，光破除一个「伪概念」还是不够的，我们需要用一个更合适的定义来代替它。在此之前，我们需要先思考一下，为什么这些「兜售者」要提出这个概念？

仔细阅读了不少相关文章之后，我发现了它们的共通之处：「遗忘临界点」通常都是「复习时机」。

也就是说，我们要提出的定义应该能指导我们设计「复习时机」。然而这是一个非常复杂的系统问题，并且有一定的主观成分，想要系统地介绍如何更精确地安排复习，本文是远远不够的。为此，我们换一个方向，看看所谓「遗忘临界点」有何客观规律：

20 m - 1 h - 8 h - 1 d - 2 d - 6 d - ……

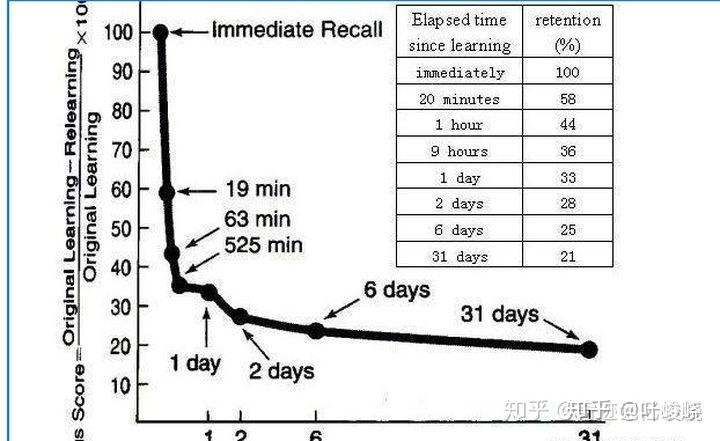
它们是逐渐递增的，并且根据这个间隔安排，遗忘的速率会变慢。那么我们就可以基于遗忘速率来重新定义一个概念：记忆稳定性。

定义1：记忆稳定性是指一批记忆在一次复习后遗忘率达到 10% 所需的时间。

可能读者会疑惑，为什么用 10% 这个数字？这个数字重要吗？我的回答是：不重要，这只是一个相对值。为了能够统一地测量不同场景下的遗忘速率，我们需要用一个值来作为标准。这个标准是 10% 还是 20%，并不影响，只要统一即可。类比一下米和英尺的关系即可。SuperMemo 提出用 10% 作为基准^[2]，而 Duolingo 则使用 50% 作为基准^[3]。我对 SuperMemo 更熟悉一些，所以也使用 10% 这个数值。

记忆稳定性能精确地描述一个记忆在何时遗忘？

显然是不行的。我在定义中特别地使用了一批记忆而非一个记忆，这不仅是基于定义本身精确性的原因，也在于使用目前使用的任何记忆观察方法都不可能给出一个记忆的遗忘速率。这是因为以下两个原因：

1. 观察者效应^[4]：我们无法在不影响被试记忆的情况下测量遗忘速率，因为想要知道被试是否还记得某条信息，我们必须对其进行询问、测试，使得下一次观察必须考虑到上一次观察产生的影响。

2. 离散型随机^[5]：对单个记忆的测试结果只有「记住」和「遗忘」两种客观结果。（当然，如果记忆材料很长，是可以测出单个记忆遗忘了百分之多少，但是会引入另一个问题：被遗忘的每一个字是否是平等的？遗忘了关键片段和遗忘了无关紧要的片段该如何区别？)

为了更好地理解上面两个原因，可以类比一下放射性元素衰变：单个具有放射性的原子核的衰变是一个随机的过程，不可能有精确的衰变时间。而对于一群放射性原子核，则可以统计出半衰期。记忆就像衰变，在统计上能够观察到遗忘速率的变化。而记忆稳定性，就类似于半衰期。

有了这个类比，是不是觉得记忆研究挺简单的？实际情况要复杂得多，放射性元素的半衰期可不会随着观察次数增多而变长，在这里我们可不能被类比所误导。

小结一下，记忆稳定性不能描述一个记忆在何时遗忘，但是可以描述一群记忆的遗忘速率。

记忆稳定性本身的难题

有了记忆稳定性，似乎遗忘速率的观察与预测已经不成问题。然而，我们回到半衰期的类比上来，就会发现另一个严重的问题：物理学家有办法把相同的放射性元素提纯出来进行测量，而记忆研究则由于以下两个原因，做不到这种提纯：

1. 记忆异质性：同样的内容让不同的人来记会有不同的遗忘速率，同一个人记忆不同的内容也会有不同的遗忘速率。如果我们只研究同一个人记忆同一个内容，就会受到之前提到的观察者效应影响，使得我们无法准确测出同一个人记忆同一个内容在不同时间间隔下的遗忘率。而研究不同人记忆不同内容，又无法保证每个记忆是同质的。

2. 记忆稳定化：其实就是观察者效应的体现。随着记住的次数变多，记忆稳定性会变高，而遗忘会降低记忆稳定性，这使得记忆稳定性在不断地变化。

记忆异质性也可以类比为，研究碳的同位素衰变时，把 C15、C16 等等不同的原子核放在一起观察，也能统计出一个整体的半衰期，但这个半衰期与混合在其中每个同位素的半衰期都不同，也不准确。

而记忆稳定化，就是完全属于记忆本身的难题了。比较著名的相关科学研究就是间隔效应^[6]和滞后效应^[7]。

小结

今天的内容差不多就到这了，如果大家有兴趣，下一次我就更深入地刨析一下记忆异质性、记忆稳定化等相关概念和规律。当然，这些都是记忆建模问题，还不涉及复习安排问题。不过记忆模型正是复习安排的基础，没有数据、模型依据的算法只能是空中楼阁。

另外，还有一些难题依然困扰着记忆算法的相关研究者，比如模型的指标、误差对复习安排的影响、记忆效率的定义等等，这都需要从业者认真思考，通过科学的方法才能给出较为符合实际的结论。

这里是对记忆研究颇有热情的学委叶哥，大家下期再会！

← 返回目录