(4/5) 高效学习的间隔重复——应用指南

总目录：

概述：https://zhuanlan.zhihu.com/p/420105707
文献综述

测试效应：https://zhuanlan.zhihu.com/p/420309917
间隔效应：https://zhuanlan.zhihu.com/p/420924493

应用指南（现在在这儿）
脚注：https://zhuanlan.zhihu.com/p/453406457

使用

当然不一定就用 SuperMemo；免费的替代方案有很多。我个人喜欢 Mnemosyne (主页)因为它是自由软件⁠，而且有 Ubuntu Linux⁠ 的版本，使用简便，有免费的移动端应用，开发已久，非常可靠（我从 2008 年就开始使用它了）。但 SRS 软件 Anki 也很受欢迎，它的优势在于功能更丰富、社区更大、更活跃（可能对东亚语言材料支持更好，移动端应用质量更高，不过移动端是专有软件）。

有了软件，那要用它做什么呢？事实上，这个问题出乎意料地难以回答。这就像「空白页面的暴政」（或空白维基）；我既然手握这股力量，这力量像机械魔像一样永不遗忘，又能随我心意让我记住一切——那我要记住什么呢？

添加多少卡片

虽说一心坚持以待功效显现已属不易，但难关还是在于决定什么知识足够有价值，需要制卡。做了一张卡片之后，在 3 年的时间里，复习这张卡片大约总共需要「30~40 秒」。理论上估计长期的复习耗时则有些繁杂。考虑一张问答卡片，每日卡片所需时间的公式为 Time = 1⁄500 × nthYear−1.5 + 1⁄30000。到了第 20 年，每天花费的时间就是 t = 1⁄500 × 20−1.5 + 1⁄3000 分钟，或者 3.557e-4 分钟。这是每天平均花费的时间，所以要想计算年均时间就将其乘以 365。假设我们想知道一张卡片在 20 年内需要多少复习时间。每日卡片所需时间每年都会变（记住，复习实践的图线类似指数衰减），所以对于每一年都要运算一次公式，之后求和；用 Haskell 语言写就是：

sum $ map (\year -> ((1/500 * year**(-(1.5))) + 1/30000) * 365.25) [1..20]

# 1.8291

总共是 1.8 分钟。（看起来数很小，但用户第一年花在复习上的时间就很少，而且用户复习时间下降得很快[55]）比如根据一位 Anki 用户 muflax 的统计数据，他的平均每张卡片复习时间为 71 秒。但假设 Piotr Wozniak 估计得太乐观了，或者我们不善于编写抽认卡，所以干脆把这个数字翻倍为 5 分钟。这是个关键的经验法则，可以用于决定什么知识要学，什么知识可以忘：如果纵观你的一生，某个知识点会让你花超过 5 分钟去查询，或者不知道这个知识点会让你损失 5 分钟，那么用间隔重复来记忆它就是值得的。5 分钟就是琐碎知识和有用知识的分界线。[56]（也许有几千张抽认卡满足这个 5 分钟规则。没关系。间隔重复能处理成千上万张卡片。参见下一章节。）

在较小程度上，可能有人好奇，着急的时候，应该间隔学习和集中学习一起用吗？目标考试或者截止日期多近的时候就不能用间隔重复了？这很难比较，因为要找到这个临界点，需要详细的指标进行比较，但对于集中重复，记忆后有 50% 机会记住所记忆的知识的平均时间似乎是 3 至 5 天。[57]，因为在这段时间里会有 2 到 3 次重复，想必一个人在回忆一个知识时会比 50% 做得更好。5 分钟和 5 天似乎是一条很好记住的经验法则：「如果你在 5 天内就需要知识，或者知识价值低于 5 分钟，就不要使用间隔重复。」

超负荷

间隔重复新手常常会添加太多内容——比如很琐碎的，或者他们完全不关注的内容。但他们很快就会遇到博尔赫斯之作《博闻强记的富内斯》⁠中的诅咒了。如果不是真心想学习软件中的材料，他们很快就会停止每天复习——因此复习会越积越多，更加令人沮丧，所以他们就干脆放弃。起码通过锻炼改善身体健康时，没有什么数字会精确而糟心地说明你落后了多少，而且从这项技术中似乎看不到收益——看起来就像无聊的抽认卡复习。

添加什么

Mnemosyne 的经典用法是记忆一些学术知识，比如地理、元素周期表、外语词汇、圣经或古兰经中的韵文、或者是浩瀚无边的医学知识。但我发现，除此之外，Mnemosyne 也很适合记忆每日一词[58]和维基词典⁠中的词，值得记忆的名言[59]⁠，生日等个人信息（或者车牌号，我以前老是记不住）之类。这些用法都很平常，但对我来说很有价值。卡片丰富多样，我每天复习时也饶有趣味。我的 Mnemosyne 里有各式各样的问题——我一会判断一段 Haskell 代码语法是否正确，一会拼读韩国谚文，然后听答案录音，一会在地图上试图找出乌克兰，一会欣赏 A.E. Housman 的某篇诗，之后又读 LessWrong 名言帖子中的名言，如此种种。其他人的用途又有百般不同；有用来是记忆学生的名字和脸的（三个例子 1 2 3），简单而实用，令我印象深刻，当然学习音符的用法也不错。

工作量

平均而言，当我学习新主题时，我每天会增加 3-20 个问题。结合我个人的记忆水平，我通常每天复习大约 90 或 100 张卡片（卡片总数超过 18,300）。复习只需要不到 20 分钟，还可以接受。（我预计实际上复习时间会更长一些，因为刚一开始学习新话题时，我还在发展卡片格式化方针，而且我也没有完备的分类系统，当然现在看我已经设计好系统了——所以我时不时就要停下来编辑卡片分类）

如果我最近没学什么新东西，复习数量会按指数方程下降，所以每日复习数量会缓缓减少。比如在 2011 年 3 月，我没学什么东西，所以从 2011-03-24 到 2011-03-26 这段时间，每日安排给我的复习数量为 73, 83, 74; 之后，复习数大约就下探到 60 多，然后再过一两周，大概下降到 50 多，这样一直到复习数变动平稳，抵达最低值，每年慢慢缩减。（我不知道这个最低是多少，因为我不添加新卡片的时间都不长）。到了 2012 年 2 月，每日复习数量是 40 多张，有时候是 50 多张，但总体上复习量还在缩减。复习量下降是真实可感的，甚至可以与原始的遗忘曲线做类比，只要让 Mnemosyne 2.0 用明年每天复习的卡片数量作图即可，即直到 2013 年 2 月（假设不添加新卡片，每天都复习等）：

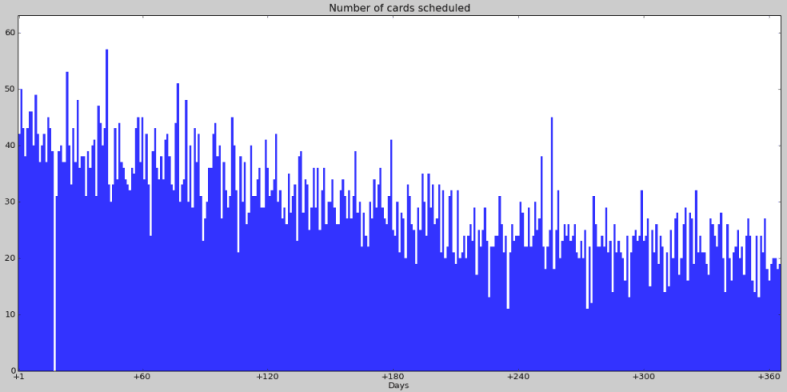
每天预测的卡片数量变化很大，但明显在减少

如果 Mnemosyne 不使用间隔重复，想要不落下这 18,300 张抽认卡的进度，非常困难。但 Mnemosyne 使用了间隔重复，跟上进度就简单多了。

18.3k 的卡片量也不至于大跌眼镜。许多用户都有一些牌组，其卡片数都在六千到七千左右，Mnemosyne 开发者 Peter Bienstman 的卡片超过八千五百张，Patrick Kenny 超过两万七千张，Hugh Chen 有个牌组有超过七万三千张卡片，在 #anki IRC 频道中，有人告诉我一个用户的牌组包含超过 20 万张卡片，以至于触发了 bug。 20 万张可能有点多，但对于正常人来说，比这少一些的卡片也是有可能的——将 SRS 牌组与一些记忆壮举比较很有趣，如记忆《失乐园》，或者记住约 80000 字的《古兰经》穆斯林 ‘hafiz’⁠ ，或者更严格的 ’Hafid‘，背诵《古兰经》和 100,000 条圣训的人。其他形式的记忆则更为强大。[60](我怀疑间隔重复在少数有充分证据证明的「超忆症」案例中涉及到了，Jill Price：阅读《连线》⁠，她对于未加准备的内容的记忆力与常人无异，同样容易遗忘，并没有可观测的解剖学差异。她的超忆症仅限于记忆「她的个人历史和某些类别，如电视和飞机失事」；此外，她是一个有强迫症特征的收集狂，记录了超过 5 万页的详细日记，这可能归咎于童年创伤，以及她将日常事件与过去事件不自主地关联起来的倾向。Marcus 说，其他超忆症的例子与 Price 相似。)

何时复习

应该在什么时候复习呢？早上？晚上？随便什么时候？证实间隔效应存在的研究没有控制复习时机这个变量，所以从某种意义上说，答：复习时机无关紧要——如果什么时候复习确实重要，那么研究中受试者复习的时机不同，间隔效应的效果也应该有显著差异。

所以什么时候方便就什么时候复习。这种便捷性让人更容易坚持，而锲而不舍比任何短期的提升远胜百倍。

要是对这个答案不满意，那么一般来说，复习应该在睡前进行。这与记忆巩固有关，已知睡眠对记忆转换成长期记忆有重要影响，而且睡眠对于睡前一段时间学习的材料强化其记忆，并且能提升创造力：有实验表明，如果老鼠的睡眠遭到打断，即使总体睡眠时间或睡眠质量保持一定，老鼠的记忆形成也受到阻碍 [61]。所以睡前复习值得推荐。（其他精神活动若是在睡前进行也有所提升；比如说，dual n-back⁠）。睡眠改善记忆的的一种可能机制，是睡前复习提升了未来需要复习或者测试的期望，因而睡眠中就会促进记忆巩固；由此观之，如果复习后立即睡觉，期望会大于选择早餐时复习，之后一天经历了许多事情，都忘了复习过卡片这回事的情形。（参见 Hartwig & Dunlosky 2012 对于学习时机和 GPA 的关系的研究）神经元增长也可能有关；来自 Stahl 2010 ：

我们对正常人类记忆形成的神经生物学取得了新进展，表明学习不是单一的事件，而是一个过程，随着时间慢慢推进。[16]⁠,[17]⁠,[18]⁠,[Squire 2003 Fundamental Neuroscience],[20] 因此，随着时间的推移重复学习的学习策略能够提高学生的记忆力就不足为奇了。[20],[21]⁠,[22⁠],[23]⁠,[24⁠],[25]⁠,[26]

…每天都有数以千计的新细胞在这个区域产生，尽管其中许多细胞在产生后的几周内就会死亡。[31]有证据表明齿状回神经元的存活率在动物学习时有所加强。学习效果好的动物比学习效果差的动物保有更多的齿状回神经元。此外，在测试 2 周后，动物在一段时间内以离散的间隔时间进行训练，记忆效果优于将同样信息一次性回顾，或者叫「集中训练」。目前尚未确定具体上何种机制将神经元存活与学习联系起来。一种理论认为，优先存活的海马神经元是那些在学习过程中以某种方式被激活的神经元。16-20[62] 在一段时间内分散学习或能更有效地促进神经元存活，因为由此一来，改变基因表达和蛋白质合成的时间加长了，而这些过程能够提升参与学习过程的神经元的寿命。

…编码阶段是在警觉的清醒状态下展开的，而为了记忆由编码阶段转移到巩固阶段，必须减小此时对记忆形成的干扰。17,18 适合这种转移的一种时段是睡眠期间，特别是非快速眼动睡眠期间，此时海马体可以与其他大脑区域交流而不受新经验的干扰。[32]⁠,[33]⁠,[34] 也许这可以解释为什么在一夜休息后会做一些决定更好，也为什么睡眠不足的情况下通宵学习，可能让你在一个小时后通过考试，但一天后却记不住材料。

前景：抽认卡拓展

现在暂且抽身片刻。我们所有大大小小的抽认卡，究竟在帮我们干什么？为什么要为「anent」这个单词以及许许多多其他单词制作抽认卡对呢？我只把词查一下也行啊。

但相比于把知识熟记在心，临时查询知识更耗时。（先忽略之前讨论的 5 分钟规则）把这件事放在计算机科学的情景中抽象地考虑便会发现，记忆还是查询的问题，涉及算法和优化领域中的经典概念——时空权衡⁠. 我们所权衡的是查找时间和有限的脑容量。

考虑一下已经给出的那种事实数据作为例子——我们可能在哪天需要知道檀香山或奥斯汀的年平均降雨量，但要记住所有首都的年平均降雨量则需要太多空间。英语单词有数百万个，但实际上超过 10 万个就太多了。更令人惊讶的是程序性知识。计算机中时空权衡的一种极端形式是用预先计算的常数代替计算。取一个数学函数，并为每个可能的输入计算它的输出。这样的输入到输出的查找表通常都非常大。想想看，对于介于 1 和 10 亿之间的所有可能的整数乘法，这样的表中会有多少个条目。但有时查找表的规模非常小（如二进制布尔函数），或者比较小（如三角函数表），或者大但还能用上（彩虹表通常从 GB 开始，很容易达到 TB）。

给定无限大的查找表，查表便可以「完全」取代加法或乘法的技能。无需计算。此时时空权衡达到了空间一侧的极端。(为达到时间一侧的极端，只要把乘法或加法定义为不知道任何计算细节的缓慢计算，如乘法表——类似于每次想要计算 2+2 时，必须掰 4 根手指。)

假设我们是想学乘法的小孩。乘法不是一条具体的原子事实，所以 SRS 和 Mnemosyne 就派不上用场了，这么说对吗？其实，从空间与时间的取舍来看，我们可以解构乘法的步骤性，而将其部分分解成原子事实，我们很容易写出脚本或者宏，以来生成随机卡片（比如说 500 张），要求计算 AB 乘以 XY 的值，并将其导入 Mnemosyne. [63]

不过，你想要做什么？是更善于计算两数相乘（两个数根据需要生成），还是记住 500 个不同的乘法问题（记忆化）？根据我自己的经验，若有多张卡片仅有微小差异，大脑很快就放弃死记硬背，而对于每张卡片单独解决问题——此时这也正是我们想要练习的。恭喜；你实现了不可能之事。

从软件工程的角度看，修改或改进卡片的需求总是会有的，而 500 段用于练习乘法的纯文本卡片颇有些难更新。所以「动态卡片」的概念就横空出世了。要在 Mnemosyne 中实现，可能是增加新的 HTML 标记，比如<eval src="">，让 Mnemosyne 把 src 参数输入 Python 解释器，并等待解释器将问题文本和答案文本包在元组里返回。之后像普通卡片一样展示问题文本，待用户思考一番，并查看答案，给作答评分。Anki 中则支持使用 Javascript, 只要在 HTML 中加入 <script>标签即可（目前只能在卡片模板直接嵌入，但也许能默认导入一些 Javascript 库），这样便能实现语法高亮，从而随心所欲地创作动态卡。

因此，对于乘法，动态卡将生成 2 个随机整数，输出类似于 x * y = ? 的问题，然后输出结果作为答案。每隔一段时间，你就会遇到新的乘法问题，随着你越来越擅长乘法计算，乘法问题出现得越少——这也是应当的。另一个数学方面⁠的想法是生成公式或程序的多个变体（其中一个选项正确，其他选项则有隐秘的错误）（译者注：即多选）；我对我的编程抽认卡是手动实现了这一点的（特别在我做练习时出错的情况，这个错误意味着有个细节需要我做几张抽认卡），但生成变体完全可以自动化。kpreid 描述了他的一个工具：

我已经编写了一个程序（是网页的形式），这个程序会生成「破损公式」，属于特化的动态卡。程序中有公式的生成器以及破损公式，运行时每次展示一些同类公式（比如∫ 2x dx = x^2 + C），但其中一个公式是破损的（比如∫ 2x dx = 2x^2 + C）。

此方法适用于可以生成随机问题或拥有大量样例的问题。可汗学院显然实现了类似动态卡的功能，将大量（算法生成的？）问题编入课程的小模块，并跟踪技能的保留情况，以便决定何时对该模块进行进一步复习。比如，你可能正在学习围棋，对学习死活⁠棋很感兴趣。这些都是可以由计算机围棋程序生成的，也可以从像 GoProblems.com⁠ 这样的地方获取。对于大量范式，围棋是旋转不变的——无论棋盘朝向如何，好的一着棋都是一样的，由于棋盘没有规定方向（就像国际象棋一样），所以好棋手应该做到无论棋盘如何白发，他都一样擅长——所以每个具体的例子都可以用另外三种方式反映出来。或者可以编写动态卡来测试「阅读」棋盘的能力，只要有像 GNU Go 这样的围棋程序说，最好的一步棋没有因为增加的噪音而改变，动态卡就会拿出每个示例棋盘/问题，并添加一些随机的棋子。

这样学习收获颇丰。编程语言可以这样学习——学习 Haskell 的人可以对 Prelude 模块或 Haskell 教科书中的所有函数，使用 QuickCheck 为这些函数生成随机参数，并将该函数及其参数输入 GHC 解释器 ghci ，看看结果是什么。围棋以外的其他游戏，如国际象棋，可能会奏效（一个现实中的例子是 Chess Tempo & LiStudy，还有查看 Dan Schmidt 的例子；或 ⁠Smash Brothers）。相当多的数学知识。如果动态卡可以访问互联网，它可以从RSS 源或只是一个网站拉下新的问题；此功能在外语学习环境中非常有用，每天都会带来一个新的句子要翻译或另一个练习。

可以借助 NLP 软件来编写动态抽认卡，这些卡能测试各种知识：如果有人混淆了动词，便在程序中输入制卡模板，如 “$PRONOUN $VERB $PARTICLE $OBJECT % {right: caresse, wrong: caresses}” ，这个模板会产生诸如 “Je Caresses le chat” 或 “Tu caresse le chat” 之类的抽认卡，测试时判断变位是否正确即可。(其中卡片的动态性有助于避免记住了特定的句子而不是变位）实现通用性极强的动态卡可能会很困难，但像模板这样的简单方法或许够用了。Jack Kinsella：

我希望有动态的 SRS 牌组可供学习语言（或其他学科）。这种牌组会统计用户复习了多少句应用了特定语法规则的句子，或者某个词汇的形式，例如词汇的单数/复数/第三人称变化/与格形式。动态 SRS 牌组会在每次复习时给用户呈现新鲜例句，避免用户记住特定答案，而促使用户应用语法规则，真正重温这个过程。此外，这些牌组能带来新意，用户也不致厌倦；变换例句中不紧要的词汇，牌组还可以提供潜移默化的词汇学习机会。这样的系统具有多层次的复习轮换，不仅可以防止过拟合学习，还可以增加每分钟学习的知识总量，这样的效率值得我投入其中。

即使这些东西看起来像是「技能」而不是「数据」！

流行度

截至 2011-05-02：

Metric	Mnemosyne	Mnemododo	Anki	iSRS	AnyMemo
首页 Alexa 排名	383k	27.5m	112k		1,766k
ML/论坛成员	461		4129/215	129
Ubuntu 下载量	7k		9k
Debian 安装量	164		364
Arch 投票	85		96
iPhone 评分	未发布		193	69
安卓评分		20	703		836
安卓安装量		100-500	10k-50k		50k-100k

SuperMemo 不适用这些评分，但在软件发布的 20 年里，SuperMemo 已经售出了数十万份：

Biedalak 是 SuperMemo World 的 CEO, 该公司销售并授权沃兹尼亚克的发明。现在，SuperMemo World 只雇佣了 25 名员工。风险投资并没有青睐，公司也没有搬到加州。2006 年，SuperMemo 的销量约为 50,000 份，多数售价不到 41 美元（共计 302006 美元）。盗版估计有更多。[66]

似乎可以放心地估计，Anki、Mnemosyne、iSRS 和其他 SRS 应用程序的市场份额加起来不到 5 万名用户（考虑到多次安装的用户、安装并放弃它的用户等可能有一些出入）。很少用户从 SuperMemo 迁移到那些新程序上，所以简单地将两个五万相加，便能合理地得出结论，SRS 的全球用户量大约在 10 万左右（但可能在 10 万以下）。

我该何去何从？

无所归依，说真的。Mnemosyne/SR 等软件只是我最喜欢的工具之一：它基于科学发现的著名效应[67]，并优雅地利用这个效应[68]，而且很有用处。SR 软件践行了启蒙运动的理想，即以理性改善人性，克服人类缺陷；SR 的思想具有数学上的严谨性，因而极富诱惑力[69⁠]。环视当下，「自我改善」共日新月异受人嘲弄，阴郁消沉纷引常人拥趸，日常生活之中，仍有此例，以证仍有拾级而上之人，实在可喜。此例比起爱迪生反反复复研发灯泡，尚显新奇有趣。

另见…

在使用 Mnemosyne 的过程中，我编写了许多脚本来生成有规律的卡片。

mnemo.hs 输入任何用换行符分隔的文本（比如诗），并生成所有可能的挖空；即，一首诗有 ABC 三句，于是生成 3 个问题：BC/ABC，A_C/ABC，AB/ABC
mnemo2.hs 和上面原理大体相同，但限制更多，主要针对较长文本，这种文本用 mnemo.hs 处理后，由于排列组合会生成太多问题；mnemo2.hs 会生成一小部分问题：对于 ABCD，生成 CD/ABCD、AD/ABCD 和 AB__/ABCD （把 2 行挖空，这样循环往复直到文本列表末尾）。
mnemo3.hs 适用于生成针对日期或名称的问题。输入「巴拉克·奥巴马 %47% 岁」，提出问题：「巴拉克·奥巴马 7/47岁」，「巴拉克·奥巴马 4/47 岁」等等。
mnemo4.hs 适用于长列表。如果你想记住美国总统的名单，自然会写出这样问题：「谁是第三任总统？/托马斯·杰斐逊」，「托马斯·杰斐逊是第__任总统。/3」，「约翰·亚当斯之后是谁？/托马斯·杰斐逊」，「詹姆斯·麦迪逊之前是谁？/托马斯·杰斐逊」。

注意，如果对每个总统都这样生成卡片，也就是有卡片正反两个角度提问总统在列表中的位置（总统 -> 位置，位置 -> 总统），也有卡片问之前的总统，之后的总统，注定会有重复的信息。mnemo4.hs 拿到列表后，是自动生成卡片的。为了更加通用，措辞会有些奇怪，但是比全部手打要强多了！（源代码的注释里有样例输出）

现在读者可能会很好奇我的 Mnemosyne 数据库是什么样子的。我经常使用 Mnemosyne，截至 2020-02-02，我的牌组中有 16,149 张（活跃）卡片。好奇的读者可以在 gwern.cards (52M; Mnemosyne 2.x 格式) 上找到我的卡片和媒体。

多年来，Mnemosyne 项目一直在收集用户提交的间隔重复统计数据。截至 2014-01-27 的完整数据集可供任何想要分析它的人下载。