对于单维刺激,人作为信息处理器时的“信道容量”[1]只有几个比特,但在日常生活中,我们似乎经常产生比这更复杂的刺激。对这种差异的一个解释是,人类的信道容量随着刺激的{维度}而{增加}。
例如,Miller 对来自 Hake 和 Garner(1951 年)以及 Coonan 和 Klemmer(与 Miller 的未发表的通信)的数据分析(1956 年,第 85-87 页)表明,人类对直线上的点的通道容量在 {3.2 和 3.9 比特(在 10-15 类的分类任务中)} 之间,而 Klemmer 和 Frick(1953 年)的数据表明,人类对矩阵中的点的信道容量约为 {4.6 比特(在约 24 类的分类任务中)}。
Miller 的图(1956 年,第 88 页)总结了来自独立变化的维度的数据:
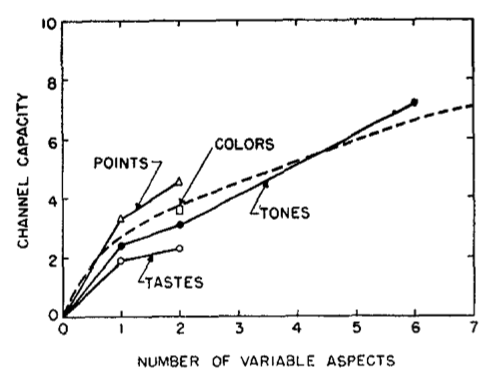
通道容量不会随着维数的增加而线性增加。事实上,随着维度的增加,只要{需要判断区分的类别的数量大于维度},任何单个变量的渠道容量都会可靠地 {减少}。(Miller, 1956, p. 89),。(Erikson, 1955, p. 327-329)
即使在所增加的维度不是独立的情况下,这种效应似乎也持续存在,例如,当同时将大小、亮度和色调与单一变量相关联时,通道容量为 4.1 比特,而任何孤立的属性为 2.7 比特(Eriksen, 1955, as aggregated by Miller, 1956, p. 88)。
Miller 猜想(1956 年,第 91 页),这种效应在 10 维左右收敛,但当时并没有证据。Halford 等人(1998 年)回顾了中间的证据,认为该效应的极限更接近于 {4}。
参考文献
Eriksen, C. W., & Hake, H. W. (1955). Absolute judgments as a function of stimulus range and number of stimulus and response categories. Journal of Experimental Psychology, 49(5), 323–332. https://doi.org/10.1037/h0044211
Hake, H. W., & Garner, W. R. (1951). The effect of presenting various numbers of discrete steps on scale reading accuracy. Journal of Experimental Psychology, 42(5), 358–366. https://doi.org/10.1037/h0055485
Halford, G. S., Wilson, W. H., & Phillips, S. (1998). Processing capacity defined by relational complexity: Implications for comparative, developmental, and cognitive psychology. Behavioral and Brain Sciences, 21(6), 803–831. https://doi.org/10.1017/S0140525X98001769
Klemmer, E. T., & Frick, F. C. (1953). Assimilation of information from dot and matrix patterns. Journal of Experimental Psychology, 45(1), 15–19. https://doi.org/10.1037/h0060868
Miller, G. A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 63(2), 81–97. https://doi.org/10.1037/h0043158 Miller - The magical number seven, plus or minus two
链接至本文(已汉化)
声明
此内容发布由 Andy Matuschak 许可。未经允许,不得转载或修改。保留所有权利。
Thoughts Memo 汉化组译制
题图:#雪ミク Dear SnowMiku - 安夏(やすなつ)的插画 - pixiv
原文:Human channel capacity increases with stimulus dimensionality (andymatuschak.org)

