KDD'22 | 墨墨背单词：基于时序模型与最优控制的记忆算法 [AI+教育]

大家好，我是叶峻峣，墨墨科技的记忆算法工程师。前三篇文章我分别介绍了我的科研经历^[1]、算法教程^[2]和研究资源^[3]。今天分享一下记忆算法论文 A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling 的详细介绍，该论文由我和哈工深的苏敬勇老师、墨墨背单词的曹译珑博士在 KDD 2022 上发表，研究了如何在背单词场景下对用户复习规划进行优化的问题。与以往的同类工作不同的是，本文构建了包含用户记忆行为时序特征的数据集，并设计了具有可解释性的记忆模型，能够在理论上保证复习策略的最优性。

论文免费下载地址：https://www.maimemo.com/paper/
复现代码仓库：https://github.com/maimemo/SSP-MMC
开源数据集：https://doi.org/10.7910/DVN/VAGUL0

1 动机

在大多数间隔重复的实践中，材料以抽认卡的形式呈现，如图 1 所示，根据简单的时间表确定每张卡片的复习时机。间隔重复调度算法有着悠长的历史。从 Leitner 盒到首个间隔重复软件 SuperMemo，他们都是以设计者的经验和个人实验为基础，使用简单的启发式算法。当今许多间隔重复软件（Anki，Mnemosyne 等）仍在使用这些算法。由于硬编码的参数和缺乏理论推导，这些算法无法适应不同的学习者和材料，性能也难以得到保证。

随着在线学习平台的普及，大量关于学生复习的数据得以收集。这使研究人员能够设计出可训练、自适应、有保证的算法。在墨墨背单词这一语言学习应用中，高效的间隔重复调度算法可以节省数百万用户的时间，并帮助他们记住更多的单词。最近，一些研究采用机器学习来确定最佳复习时间。然而，由于以下三个原因，这些方法并不适用于我们的情况：

缺少时间序列信息：一些研究，如 HLR（半衰期回归）模型和 EFC（指数遗忘曲线）模型，使用遗忘曲线将回忆概率与上次复习后的时间联系起来。但他们忽略了时间间隔对记忆强度的影响。在他们的模型中，记忆强度是关于重复次数的函数。根据间隔效应和我们收集的数据，复习间隔对长期记忆的形成过程有很大影响。
缺少用户感知的优化目标：HLR 和基于它改进的 C-HLR 模型，旨在准确预测记忆的回忆概率。而用户更关心复习压力、记忆效率等指标。
缺少可解释性：一些基于深度强化学习的算法对设计者来说是黑盒子，缺乏可解释性。可解释的学生记忆模型对教育研究更有意义。

在本文中，我们根据收集到的数以百万计的记忆数据，建立了用于模拟用户长期记忆的 DHP（Difficulty-Halflife-P(recall)）模型。我们设定了具有实际意义的优化目标：最小化用户形成长期记忆的成本。为了实现这一目标，我们提出了一种新颖的间隔重复调度算法，名为 SSP-MMC（Stochastic-Shortest-Path-Minimize-Memorization-Cost）。

我们的工作为间隔重复调度算法提供了更接近自然环境的长期记忆模型，并通过现实世界的数据进行了测试。我们找到了间隔重复调度的优化问题和相应的最优方法。我们公开了数据和代码工具，以方便复现和后续研究。综上所述，本文的主要贡献是：

建立并开源我们的间隔重复日志数据集，这是首个包含时间序列信息的数据集。
据我们所知，这是首个采用时间序列特征来模拟长期记忆的工作。
实验结果表明，在最小化记忆成本方面，SSP-MMC 优于最先进的基线。

2 长期记忆模型

为了设计一种高效、有保证、可解释的间隔重复调度算法，我们收集了学习者的记忆行为数据，然后用这些数据来验证几种心理效应。利用这些效应，我们对记忆进行建模，以了解间隔重复调度如何影响学习者的记忆状态。

2.1 建立数据集

我们在墨墨背单词上收集了一个月的学习日志，从中筛选出 2.2 亿条记忆行为数据，用于训练模型来模拟学习者的记忆。由于以下原因，我们没有使用 Duolingo 的开源数据集：

它缺乏时间序列方面的信息，如反馈和间隔的序列，而我们对数据的分析表明，不同的序列对记忆状态有很大的影响。
它对回忆概率的定义有问题。Duolingo 将回忆概率定义为一个单词在复习环节中被正确回忆的次数比例，即假定同一单词在复习环节中的多次记忆行为相互独立。然而在实践中，第一次回忆会影响学习者的记忆状态和后续记忆。

从墨墨背单词收集的记忆数据记录了学习者对单词记忆的历史信息。对于任意记忆行为，我们用一个四元组来表示：

$e :=(u, l, t, r)$

其含义为一个学习者 $u$ 在时刻 $t$ 回忆单词 $l$ 并反馈 $r$ （回忆成功 $r=1$ ；回忆失败 $r=0$ ）。

为了便于研究记忆行为序列，我们将历史特征加入其中：

$e_{i} :=(u, l, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol r_{1:i-1} , \Delta t_i , r_i)$

其中 $e_i$ 表示学习者 $u$ 对单词 $l$ 的第 $i$ 次回忆， $\Delta t$ 表示两次回忆之间的时间间隔。 $\boldsymbol \Delta t_{1:i-1}$ 和 $\boldsymbol r_{1:i-1}$ 分别表示第 $1$ 到第 $i-1$ 回忆的间隔历史和反馈历史。

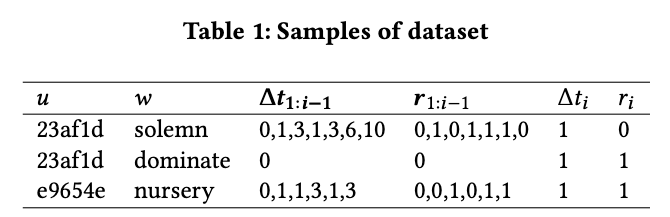
我们过滤掉其中第一个反馈为 $r=1$ 的日志，以排除学习者在使用间隔重复之前形成的记忆的影响。学习者的记忆行为事件的样本日志见表 1

由此我们得到了包含任意学习者对任意单词的完整记忆行为历史数据。接下来，我们将基于该数据验证两个在间隔重复中发挥重要作用的心理学现象。

2.2 遗忘曲线与间隔效应

遗忘曲线是说，学习者停止复习后，记忆会随着时间的推移而衰退。在上面的记忆行为事件中，回忆是二元的（即，用户要么完全回忆起一个单词，要么忘记一个单词）。为了捕捉记忆的衰退，我们需要得到二元回忆背后潜在的概率。为了得到回忆概率，我们忽略学习者本身的影响，用学习该单词的学习者中的回忆比例 $\cfrac{n_{r=1}}{N}$ 作为回忆概率 $p$ ，从而聚合得到：

$e_{i} :=(l, \boldsymbol{\Delta t}_{1:i-1}, \boldsymbol r_{1:i-1}, \Delta t_i , p_i)$

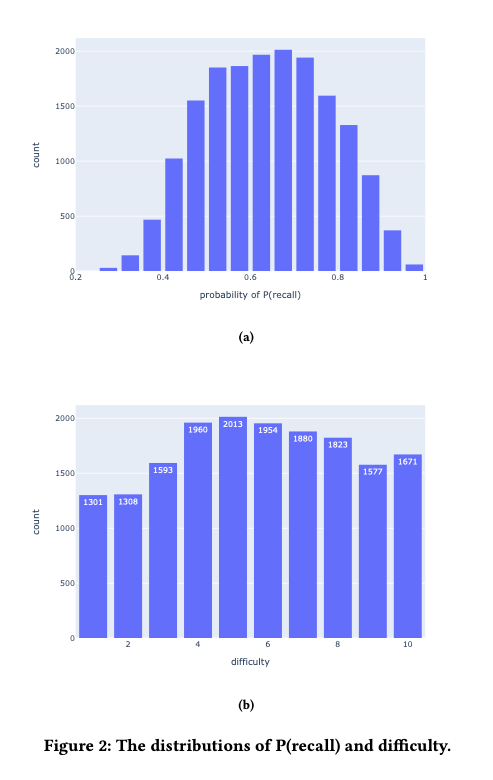
通过控制 $w$ 、 $\boldsymbol{\Delta t}_{1:i-1}$ 和 $\boldsymbol r_{1:i-1}$ ，我们可以绘制每个 $\Delta t$ 的 $p$ ，从而得到遗忘曲线。当 $N$ 足够大时，比率 $n_{r=1}/N$ 接近回忆概率。然而，墨墨背单词中有将近 10 万个单词，在不同的时间序列中为每个词收集的行为事件是稀疏的。我们需要对单词进行分组，以便在区分不同的单词和缓解数据稀疏性之间做出权衡。鉴于我们对遗忘曲线感兴趣，材料的难度会明显影响遗忘速度。因此，我们尝试用第一次学习它们后第二天的回忆率作为划分单词难度的标准。图2a描绘了回忆率的分布。

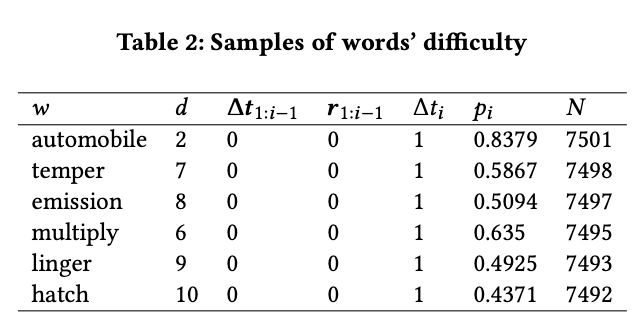
我们可以从数据分布中看到，回忆率大多在 0.45 和 0.85 之间。为了让分组尽可能均衡，我们将单词分为十个难度组。分组的结果显示在图2和表2中。符号 $d$ 表示难度，数字越大，难度就越大。

因此，分组后的记忆行为事件可以表示为：

$e_{i} :=(d, \boldsymbol{\Delta t}_{1:i-1}, \boldsymbol r_{1:i-1}, \Delta t_i , p_i)$

使用聚合后的数据，我们便可以绘制有足够数据支持的遗忘曲线。我们使用指数遗忘曲线模型 $p_i = 2^{-\frac{\Delta t_i}{h_i}}$ 对其进行拟合，并由此得到记忆半衰期。

通过此方法，我们将 $\Delta t_i , p_i$ 特征降维得到 $h_i$ ：

$e_{i} :=(d, \boldsymbol{\Delta t}_{1:i-1}, \boldsymbol r_{1:i-1}, h_i)$

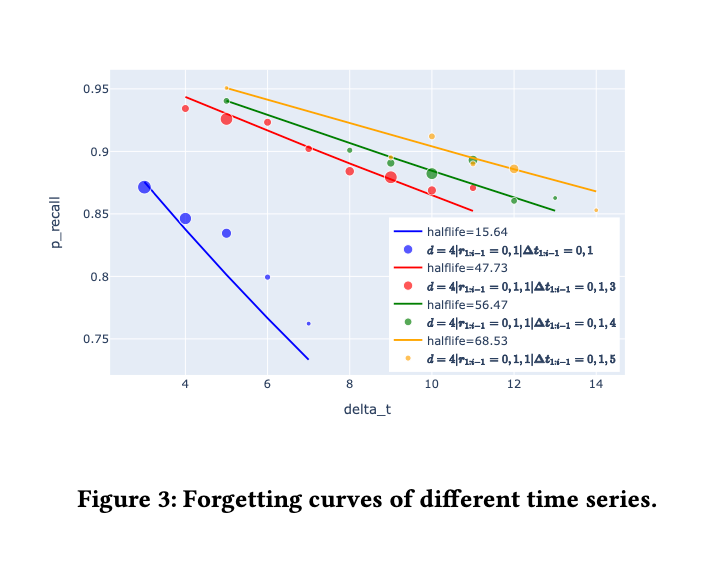
间隔效应是说，随着复习之间的间隔增长，复习后对记忆的巩固效果也会提升。在我们的数据集中，我们认为可以用一次复习前后的半衰期之比来表示记忆的巩固效果。

图 3 中的散点反映了每个区间所对应的回忆比例，而曲线是用指数函数拟合这些点的结果。各种颜色表示不同的控制情况。从各种记忆行为事件中，我们可以观察到，成功的回忆会提高记忆的半衰期。记忆巩固的效果随着复习间隔的增长而上升。

基于上述效应，我们提出了 Difficulty-Halflife-P(recall) Model，用于解释现有数据。

2.3 Difficulty-Halflife-P(recall) 模型

目前处理时间序列数据的先进方法是基于 LSTM 和 GRU 等循环神经网络，它们可以利用时间序列特征预测半衰期。然而，引入神经网络将使我们的算法缺乏解释性。因此，我们建立了一个满足马尔可夫性的时序模型，以满足可解释性和简单性。在这个模型中，我们将时间序列降维成状态变量和状态转换方程。我们考虑以下四个状态变量：

半衰期。它衡量记忆的存储强度。
回忆概率。它衡量记忆的检索强度。根据间隔效应，每次复习的间隔时间会影响半衰期。当 $h$ 固定时， $\Delta t$ 和 $p$ 是一一映射的，为了规范化，我们用 $p=2^{-\Delta t/h}$ 代替它作为状态变量。
回忆结果。回忆成功后半衰期提高，回忆失败后半衰期下降。
难度。直觉上难度越高，记忆越难巩固。

将时间序列投影到三维空间，回忆前的半衰期、回忆概率和回忆后的半衰期分别对应 XYZ 轴，难度由颜色表示，如图 4 所示。

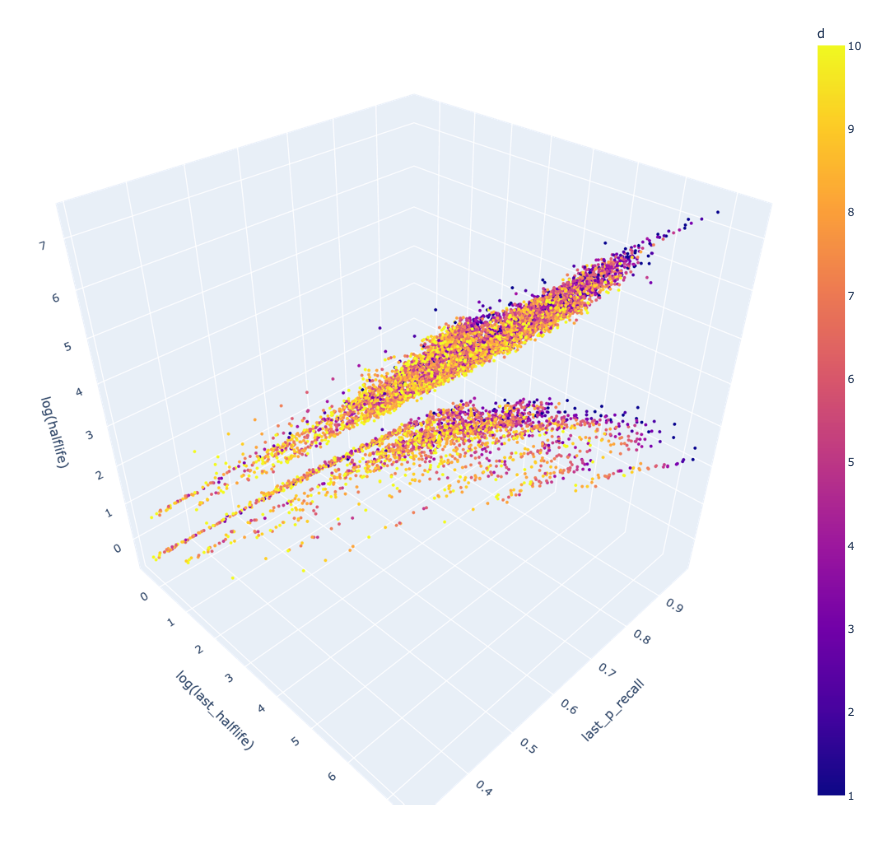
通过观察数据的分布，我们观察到了两个现象：在 $r_1 = 1$ 时 $h_{i+1}>h_i$ ，在 $r_1 = 0$ 时 $h_{i+1}>0$

我们将这两个约束条件考虑到状态转移方程中，得到：

$h_{i+1} =[h_i \cdot (\exp( \boldsymbol \theta_1 \cdot \boldsymbol x_i)+1),\exp(\boldsymbol \theta_2 \cdot \boldsymbol x_i)] \cdot [r_i, 1-r_i]^T$

其中

$\boldsymbol x_i = [\log d_i, \log h_i,\log(1-p_i)]$ 是特征向量
$\boldsymbol\theta$ 是参数向量，由线性回归得出

在该转移方程的基础上，我们观察到，当学习者反馈遗忘后的记忆行为中，在当前半衰期和回忆概率相同的情况下，下一个半衰期变小。我们认为这是由于对学习者来说更难的材料，更可能被反馈遗忘，所以学习者反馈遗忘后的材料，其难度会比记住的材料更高。

因此，我们增加了一个状态转移方程：

难度转移方程： $d_{i + 1} = [d_i, d_i + \theta_3]\cdot[r_i, 1-r_i]^T$

为了防止难度无限增长，我们增加了一个上限。

最终，我们的记忆状态转移方程组为：

$\left[\begin{array}{c} h_{i+1} \\ d_{i+1} \end{array}\right] = \left[\begin{array}{c} h_i \cdot (\exp( \boldsymbol \theta_1 \cdot \boldsymbol x_i)+1)&\exp(\boldsymbol \theta_2 \cdot \boldsymbol x_i)\\ d_i& d_i + \theta_3 \end{array}\right]\times\left[\begin{array}{c} r_i \\ 1-r_i \end{array}\right]$

$\boldsymbol x_i = [\log d_i, \log h_i,\log(1-p_i)]$

$r_i \sim Bernoulli(p_i)$

$p_i=2^{-\frac{\Delta t_i}{h_i}}$

根据上述转移方程组，和数据中统计出的半衰期初始值 $h_0$ 、难度初始值 $d_0$ ，即可预测任意记忆行为序列下的半衰期 $h_i$ 。计算过程如图 5 所示。

3 最优调度

有了描述学习者长期记忆的模型，我们便可以使用该模型来预测不同间隔重复调度算法的表现。在进行优化调度之前，我们需要设置一个优化目标。

3.1 问题设置

间隔重复方法的目的在于帮助学习者高效地形成长期记忆。而记忆半衰期反映了长期记忆的存储强度，复习次数、每次复习所花费的时间则反映了记忆的成本。所以，间隔重复调度优化的目标可以表述为：在给定记忆成本约束内，尽可能让更多的材料达到目标半衰期，或以最小的记忆成本让一定量的记忆材料达到目标半衰期。其中，后者的问题可以简化为如何以最小的记忆成本让一条记忆材料达到目标半衰期，即最小化记忆成本（Minimize Memorization Cost, MMC）。

我们在 2.3 节所构建的长期记忆模型满足马尔可夫性，每次记忆的状态只取决于上一次的半衰期、难度和当前的复习间隔和回忆结果。其中回忆结果服从一个与复习间隔有关的随机分布。由于半衰期状态转移存在随机性，一条记忆材料达到目标半衰期所需的复习次数是不确定的。因此，间隔重复调度问题可以视作一个无限时间的随机动态规划问题。考虑到优化目标是让记忆半衰期达到目标水平，所以本问题存在终止状态，所以可以转化为一个随机最短路径问题（Stochastic Shortest Path, SSP）。结合优化目标，我们将算法命名为 SSP-MMC。

3.2 随机最短路径算法

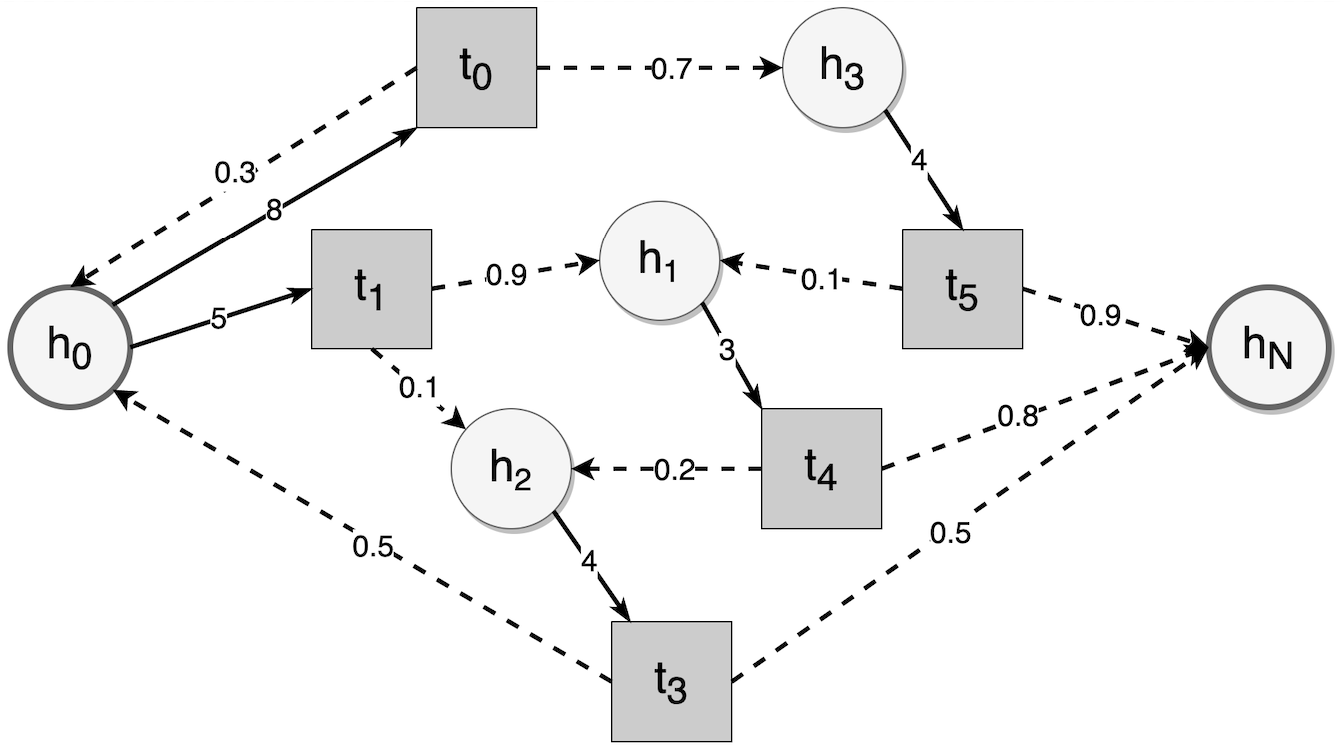
如上图所示，在不考虑难度状态的情况下，圆圈是半衰期状态，方块是复习间隔，虚线箭头表示给定复习间隔的半衰期状态转换，黑边表示给定记忆状态下可用的复习间隔与相应的复习成本。间隔重复中的随机最短路径问题是调度算法如何给出最佳复习间隔，以最小化达到目标半衰期的预期复习成本。

符号约定：

$h_0$ - 初始半衰期
$h_{N}$ - 目标半衰期
$h_{k+1}, d_{k+1} = f(h_k,d_k,\Delta t_k, r_k)$ - 记忆状态转移方程
$g(h_k,d_k,\Delta t_k, r_k)$ - 复习成本
出于简化的目的，我们只考虑 $r_k$ 的影响： $g(r_k) = a \cdot r_k + b \cdot (1-r_k)$

a 为回忆成功的成本
b 为回忆失败的成本
通常回忆失败后需要更多的练习，所以 b > a

$\Delta T(h_k,d_k)$ - 当前记忆状态下可选的复习间隔集合
$J_\pi(h_0,d_0)$ - 总复习成本

让我们列出 SSP-MMC 的 Bellman 方程：

$J(h_k,d_k) = \min\limits_{\Delta t_k \in \Delta T(h_k, d_k)} E[g(r_k) + J(f(h_k,d_k,\Delta t_k, r_k))]$

基于该方程，可以使用动态规划迭代求解，得到每个 $h_k,d_k$ 对应的最优复习间隔 $\Delta t_k$ 。

考虑到 $h$ 是一个连续值，不利于记录状态，可以将其离散化：

$h_{index} = \lfloor\log(h) / \log(\rm{base})\rfloor$

base 用于控制 h 分箱大小
取对数是因为状态转移方程中，h 近似于指数增长

由于存在难度上限 $d_N$ 和终止半衰期 $h_N$ ，我们可以建立一个成本矩阵 $J[d_N][h_N]$ ，并初始化为 $\inf$ 。设置 $J[d_i][h_N] = 0$ ，然后开始遍历每个 $(d_k,h_k)$ ，从 $\Delta T(h_k, d_k)$ 中遍历每个 $\Delta t_k$ ，计算 $p_k,h_{r_k=1},h_{r_k=0},d_{r_k=1},d_{r_k=0}$ ，然后使用以下公式：

$cost[h_k][d_k] = \min\limits_{p_k} [p_k \cdot (g(1) + cost[h_{r_k=1}][d_{r_k=1}]) + (1-p_k) \cdot (g(0) + cost[h_{r_k=0}][d_{r_k=0}])]$

来迭代更新每个记忆状态对应的最优成本。用一个策略矩阵记录每个状态下最优的复习间隔。最优策略会在一遍遍迭代中收敛。

4 实验

我们的实验将回答以下问题：

DHP 模型模拟长期记忆的效果如何？
DHP 模型的权重参数的实际意义是什么？
SSP-MMC 算法给出的最佳复习间隔的模式是什么？
与基线相比，SSP-MMC 算法在不同指标上有什么改进？

在这一节中，我们首先根据第 2.3 节中收集的数据集训练了 DHP 模型，并将其与 HLR 模型进行比较。还对 DHP 模型的参数进行了可视化，以获得对记忆的直观解释。然后，我们使用 DHP 模型作为 SSP-MMC 算法的训练环境，以获得最佳策略并将其可视化。最后，我们在由 DHP 模型组成的模拟环境中比较了 SSP-MMC 与不同基线的性能。

4.1 DHP 模型权重分析

为了更好地了解DHP模型，我们将其与 HLR 模型在预测半衰期方面进行比较，并分析模型的权重。

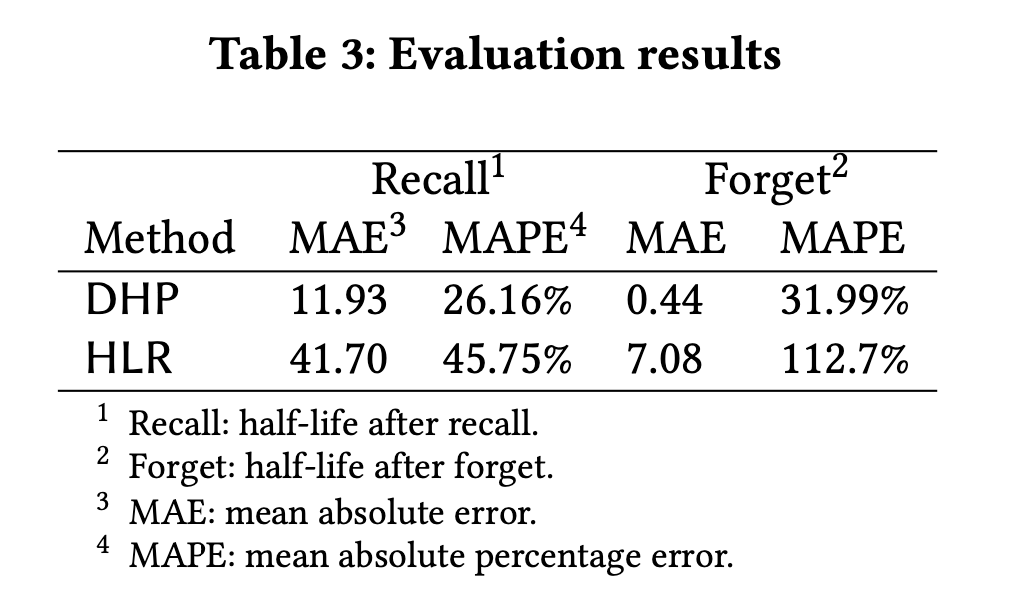
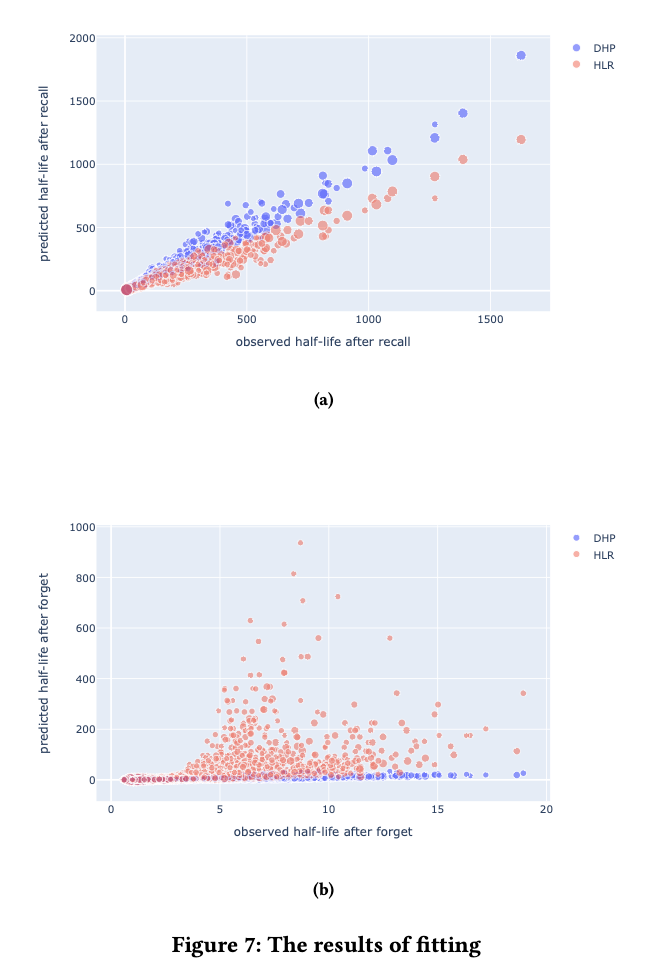
拟合的结果显示在图 7 中。从比较中，我们可以发现，在预测半衰期时，HLR 是欠拟合的，而 DHP 模型的预测误差（如表所示）明显小于 HLR 模型，特别是在回忆失败后的结果。这很可能是由于 HLR 丢失了时间序列信息，使得它无法区分 $r_{1:2}=1,0$ 和 $r_{1:2}=0,1$ 这样的记忆行为。

根据拟合得到的参数和模型的方程，我们得到成功回忆后的半衰期：

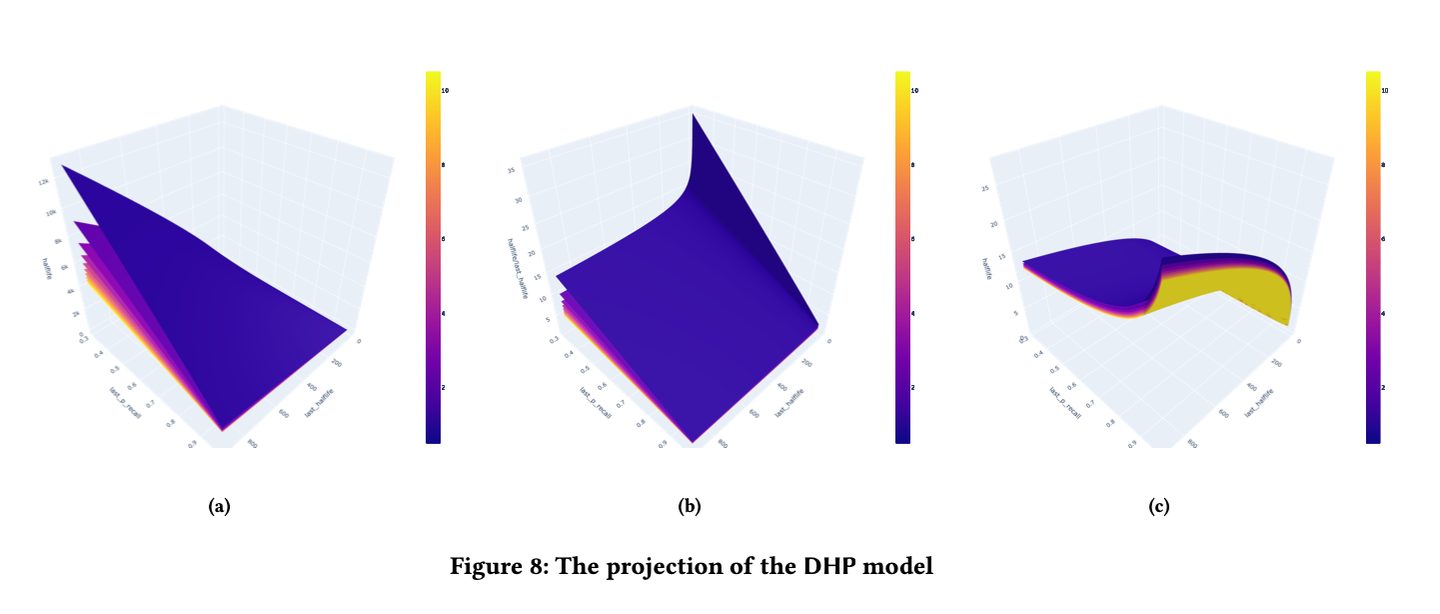
$h_{i+1} = h_i \cdot( \exp(3.81) \cdot d_i^{-0.534} \cdot h_i^{-0.127} \cdot (1 - p_i)^{0.970} + 1)$

图 8a 说明，成功回忆后的半衰期随着 $p_i$ 的减少而增加，这验证了间隔效应的存在。图 8b 显示，随着最后半衰期的增加，半衰期的增加倍数减少，这可能意味着我们的记忆巩固会随着记忆强度的增加而减少，即存在边际效应。

类似地，回忆失败后的半衰期：

$h_{i+1} = \exp(-0.041) \cdot d_i^{-0.041} \cdot h_i^{0.377} \cdot (1 - p_i)^{-0.227}$

图 8c 中，记忆的半衰期越长，回忆失败后的半衰期也越长，这可能是因为记忆在遗忘中没有完全丢失。而随着回忆概率的降低，回忆失败后的半衰期也随之降低，这可能是因为随着时间的推移，记忆被遗忘得更彻底。

4.2 SSP-MMC 最优策略分析

通过在 DHP 模型的环境中训练算法 SSP-MMC，我们得到了每个记忆状态的预期复习成本和最佳复习间隔。

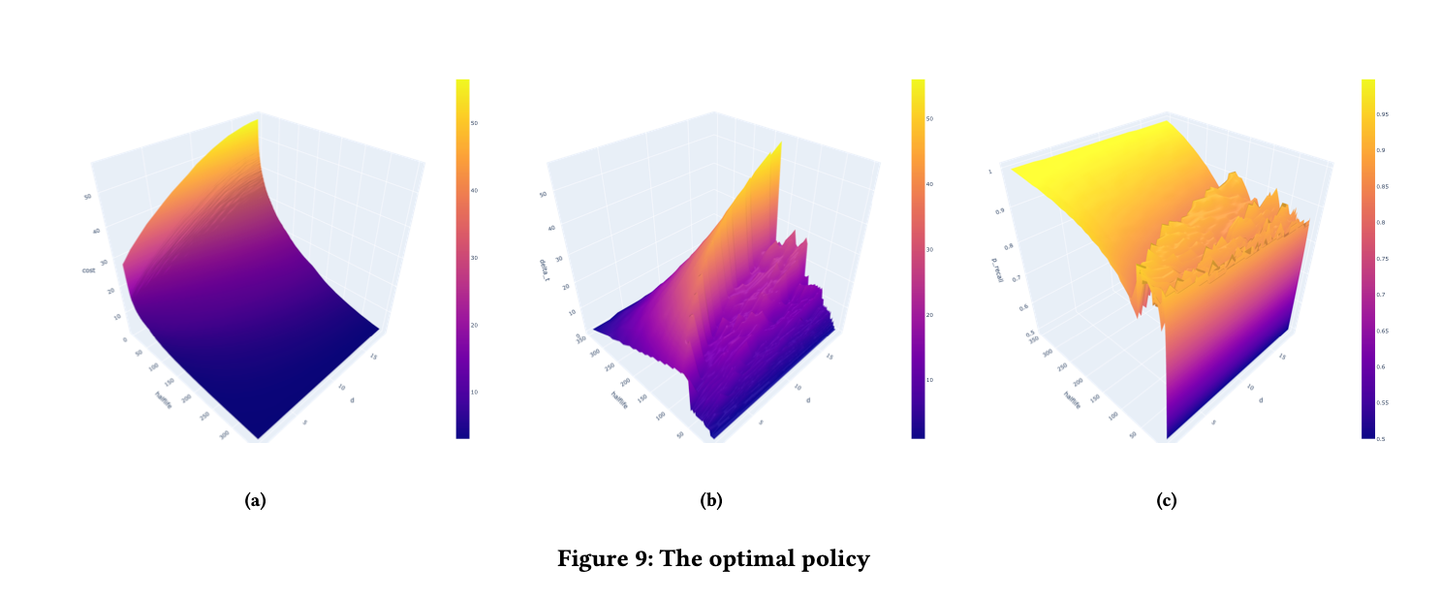
如图 9(a) 所示，复习成本随着半衰期的增加而减少，随着难度的增加而增加。具有高半衰期的记忆以较低的预期成本达到目标半衰期。此外，难度较高的记忆具有较高的预期成本，因为它们的半衰期增长较低，如图 8(b) 所示，需要更多的复习才能达到目标半衰期。

如图 9(b) 所示，在相同的记忆半衰期水平下，间隔时间随着难度的增加而增加。这可能是因为遗忘提高了简单记忆的难度，降低了它们的半衰期，导致了更高的复习成本。调度算法倾向于给简单记忆更短的间隔时间，减少它们被遗忘的概率，即使它牺牲了一点半衰期的提升。间隔时间在半衰期的中段达到峰值。为了解释这个峰值，有必要与图 9(c) 进行比较。

如图 9(c) 所示，对应于最佳间隔的回忆概率随着半衰期的提高而增加，随着难度的增加而减少。这意味着在记忆的早期阶段，调度器会指示学习者以较低的检索强度进行复习，这可能是「合意困难」的反映。当半衰期增加到目标值时，回忆概率就会接近 100％。根据公式 $\Delta t = - h \cdot \log_2 p$ 和 p 对 h 的趋势， $\Delta t$ 在出现峰值的地方先是增加，然后减少。

4.3 离线模拟

我们研究了 5 个基线策略：RANDOM、ANKI、HALF-LIFE、THRESHOLD、MEMORIZE 和 3 个指标：目标半衰期达成量（THR）、累计学习量（WTL）、回忆期望（SPR）。

环境

我们的模拟环境有以下参数。目标半衰期 $h_N$ ，回忆成功/失败成本，每日成本限制和模拟持续时间。

基线

我们将 SSP-MMC 与几个基线调度算法进行对比：

RANDOM 策略，每次从 $[1,h_N]$ 中随机选择一个间隔进行安排复习
ANKI，SM-2 的一种变体，参考其开源的代码。由于 ANKI 的算法中，用户的回忆结果是以 1-4 分输入。我们将回忆失败映射到 1 分，回忆成功映射到 3 分。
HALF-LIFE，即直接以半衰期作为本次安排的复习间隔。
THRESHOLD，即当 p 小于等于某一阈值（我们使用 80%）时进行复习。
MEMORIZE，一种基于最优控制的算法，代码来自于他们开源的仓库。

指标

我们的评价指标包括：

THR，达到目标半衰期的记忆数量
SPR，累计回忆期望，即学习者所有记忆的单词的回忆概率之和。
WTL，累计学习数量

实现细节

我们设定 360 天（接近一年）的回忆半衰期为目标半衰期，当单词的半衰期超过这个值时，它将不再被安排复习。然后，考虑到实际场景中学习者每天的学习时间大致恒定，我们设定 600s（10 分钟）为每天学习成本的上限。当每次学习和复习过程中的累计成本超过这个上限时，无论是否完成，复习任务都会被推迟到第二天，以确保每种算法在相同的记忆成本下进行比较。我们使用学习者的平均时间，即成功回忆的时间为 3s，失败回忆的时间为 9s。然后，语言学习是一个长期的过程，我们设定模拟时间为 1000 天。

分析

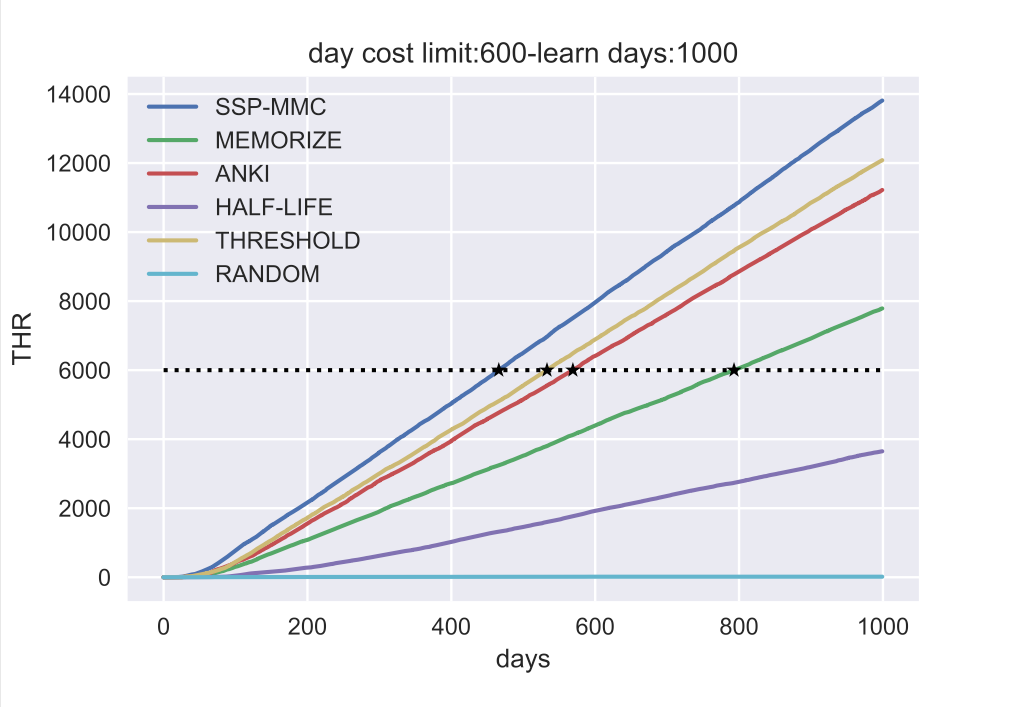
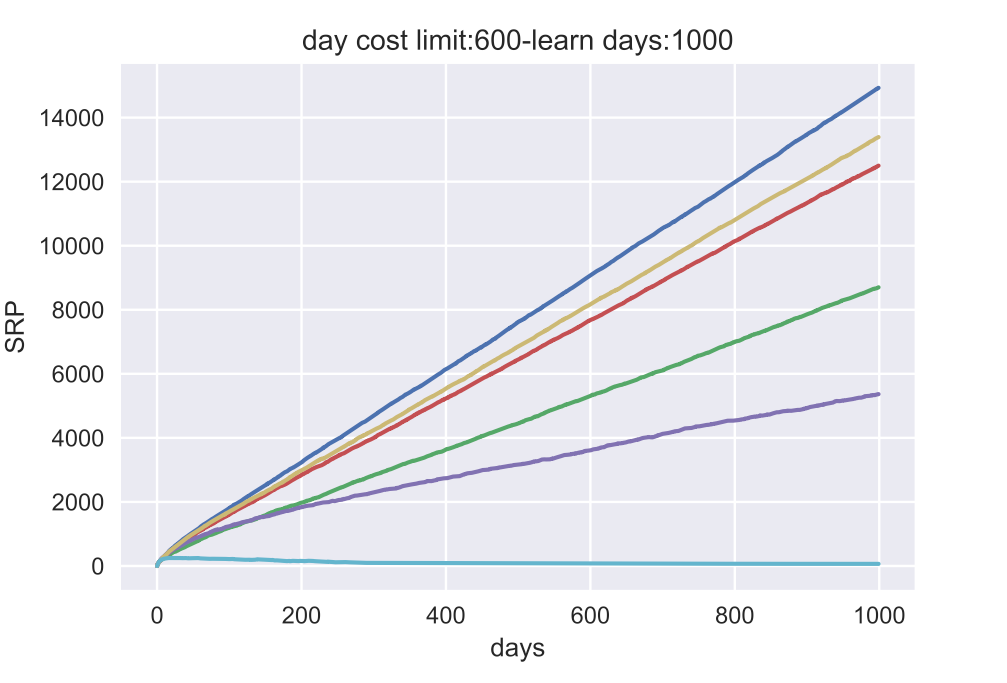
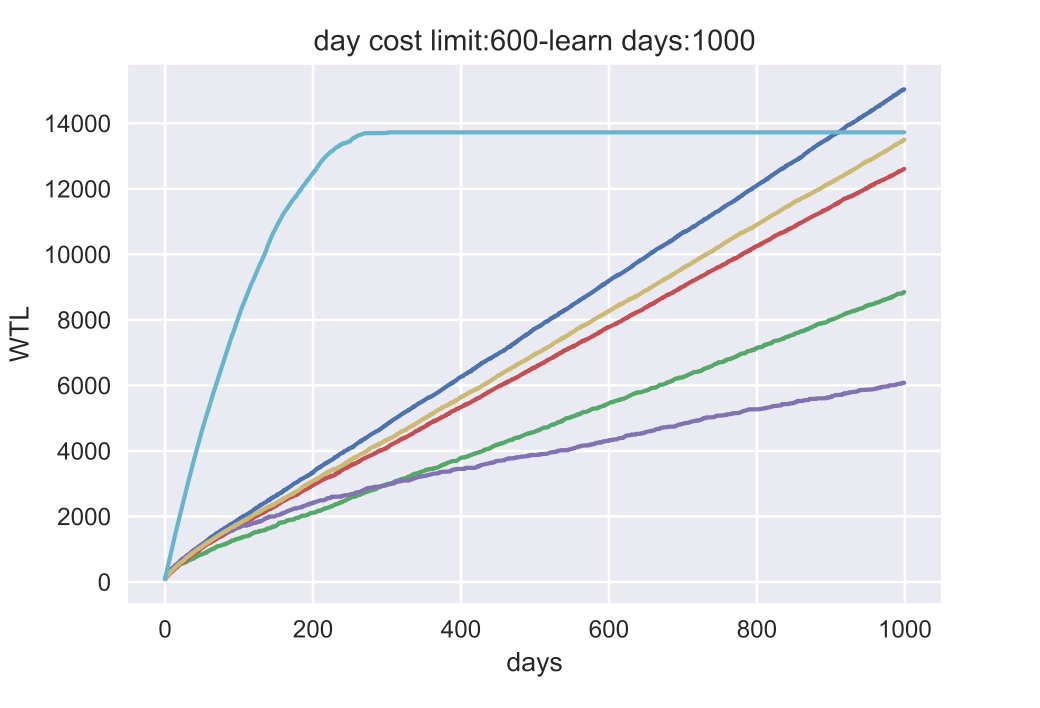
上图中的仿真结果显示，

在 THR 上， SSP-MMC 的表现比所有基线都好，这在意料之中。THR 与 SSP-MMC 的优化目标一致，而且 SSP-MMC 可以达到这个指标的上限。

为了量化每种算法表现之间的相对差异，我们比较了 THR = 6000 的天数（图中标记为 $\star$ ）： SSP-MMC 为 466 天，ANKI 为 569 天，THRESHOLD 为 533 天，而 MEMORIZE 为 793 天。与THRESHOLD 相比，SSP-MMC 节省了 12.6％的复习时间。

SRP 上的结果与 THR 上的结果相似。这意味着学习者按照 SSP-MMC 安排学习会记得最多。

在 WTL 上，RANDOM 在早期阶段击败了所有的算法，因为只要调度算法不安排复习，学习者就可以继续学习新的单词，但这是以忘记已经学过的单词为代价的。此外，SSP-MMC 胜过其他基线，因为它将记忆的成本降到最低，给学习者更多的时间来学习新词。

5 结论

我们的工作建立了第一个包含完整时序信息的记忆数据集，设计了基于时序信息的长期记忆模型，能够良好拟合现有的数据，并为优化间隔重复调度提供了坚实的基础。我们将最小化学习者的记忆成本作为间隔重复算法的目标，根据随机最优控制理论，我们推导出了有数学保证的最小化记忆成本的调度算法 SSP-MMC。SSP-MMC 将心理学上被多次验证的遗忘曲线、间隔效应等理论与现代机器学习技术相结合，降低了学习者形成长期记忆的记忆成本。相较于 HLR 模型，考虑时序信息的模型在拟合用户长期记忆上的精度有显著提升。并且，基于随机动态规划的间隔重复调度算法，在各项指标上都超过了之前的算法。该算法部署在墨墨背单词中以提高用户的长期记忆效率。我们在附录中提供了设计和部署的技术细节。

主要的后续工作是改进 DHP 模型，考虑用户特征对记忆状态转移的影响，并在语言学习以外的间隔重复软件中使用我们的算法来检验模型的通用性。此外，学习者使用间隔重复方法的场景十分多样化，设计匹配学习者目标的优化指标也是一个值得研究的问题。

补充：本文的算法经简化后，已可以与 Anki 等间隔重复软件相兼容，具体请见我为 Anki 开发的算法插件：

open-spaced-repetition/fsrs4anki: A modern Anki custom scheduling based on free spaced repetition scheduler algorithm (github.com)

参考

1. 我是如何在本科期间发表顶会论文的？ ./543325359.html
2. 间隔重复记忆算法：e 天内，从入门到入土。 ./556020884.html
3. 间隔重复记忆算法研究资源汇总 ./561539418.html

专栏：学委叶哥的随笔

← 返回目录