所谓「以绝大数人努力程度之低,根本没有要到拼天赋的地步」这种说法,在基础教育领域完全就是扯淡。
实际上,更符合实际的说法是:以绝大多数人所受的教育方法效果之低,根本没有到受限于天赋差异的地步。
虽然每个人在工作记忆容量和学习速度上的差异确实存在,且会影响学习效率,但绝大多数人未达潜力上限的主因并非努力总量不足,而是教育方法和练习策略的严重错误——知识漏洞的放任、无效练习的常态化、对学习速度差异的漠视。
一、知识漏洞的「滚雪球效应」:教育系统放任基础崩塌
传统课堂以统一进度推进教学,缺乏分层递进机制,导致学生的前置知识尚未牢固,就要被迫学习新课,形成「知识缺口→理解障碍→更多缺口」的恶性循环。
二、无效练习的「伪努力陷阱」:教学实践忽视认知规律
过度依赖「熟能生巧」的机械训练(如单向讲授、重复刷题),混淆训练强度与训练质量,忽视认知负荷理论指导下的结构化练习设计和刻意练习。
三、学习速度的「标准化暴政」:集体授课否定个体认知节奏
固守「一刀切」的教学进度,既不承认工作记忆容量的天然差异,也不为慢速学习者提供额外练习时间,反而将进度滞后归咎于「天赋不足」。
四、总结:教育系统的「原罪」与革新方向
当前教学体系的核心矛盾在于:用工业化时代的标准化生产模式应对信息化时代的个性化发展需求。这造成三重异化:
- 潜力误判:将教育缺陷导致的挫败归因为「天赋不足」;
- 资源错配:大量精力消耗在低水平重复训练,挤占思维发展空间
- 机会剥夺:未向慢速学习者提供足够的练习机会,变相制造「努力无效」的假象。
真正的教育公平应体现为:承认认知差异的客观存在,并通过科学方法(精熟学习、刻意练习、弹性进度)最大化每个学生的潜在成就。
当教育方法符合认知规律时,「学习列车」上的乘客远比我们想象的更多。
以上内容为 DeepSeek-R1 对 @Thoughts Memo 的译文《第七章 个体差异:学习过程中的迷思与现实》的总结,以下是译文原文。
⠀⠀⠀摘要:在学习过程中,个体之间确实存在差异,但这种差异主要体现在工作记忆容量和学习速度上,而非所谓个人偏好的「学习风格」。事实上,不同的学习者需要的是相同形式的练习,只是所需的练习量有所不同。尽管并非每个人都能掌握高深的数学知识,但大多数人都有能力学习基础数学。然而在现实中,很少有人能充分发挥他们的数学潜力,因为他们在早期就因基础不扎实、无效的练习习惯、缺乏进一步练习的能力或意愿,以及缺乏动机等因素而偏离了学习轨道。
个体间的差异在于学习速度,而非学习风格
迷思:每个人的工作记忆容量和学习速度基本相同,学习效果的差异主要源于个人偏好的学习风格不同。
现实:事实恰恰相反。个体间的工作记忆容量和学习速度通常存在显著差异。虽然人们可能有自己偏好的学习「风格」(如视觉型或语言型),但实际上在采用符合个人偏好的信息传递方式时,并没有提高学习效果。常见的误解是认为不同的人需要数量相同但形式不同的练习,而实际情况是:不同的人需要相同类型的练习,只是所需的练习量不同。
| 学习风格偏好并不重要
「学习风格」理论是教育领域最广为人知,同时也是被最全面地揭穿的神经迷思之一。这一理论认为,学习者在接收符合自己偏好的「学习风格」的内容时,学习效果会更好。然而,事实并非如此。让我们来看看在一项关于神经迷思持续存在的大型综合研究中的观点(Betts et al., 2019):
⠀⠀⠀「学习风格理论是教育领域最广为流传的迷思之一(Pashler, McDaniel, Rohrer & Bjork, 2008; Reiner & Willingham, 2010; Roher & Pashler, 2012)。尽管相关假设已经被多次检验,但至今没有证据表明个体在接受符合其偏好学习风格的信息时,学习效果会更好(Newtown & Miah, 2017)。
⠀⠀⠀……
⠀⠀⠀2006 年,一群出资人发起了一项学习风格挑战,最初悬赏 1000 美元,后来提高到 5000 美元,旨在寻求能够支持这一理论的科学证据(Wallace, 2014)。然而,直到现在,这笔奖金仍无人领取。」
Grospietsch & Lins (2021) 对此作了深入阐述:
⠀⠀⠀「Grospietsch 和 Mayer (2021b) 指出,这个神经迷思的确有一定事实基础:人们对接收信息的方式有着差异性的偏好,例如有些人偏好视觉信息,有些人则偏好语言信息(参见 Höffler et al., 2017 的研究)。
⠀⠀⠀然而,基于这一事实,人们得出了以下三个错误结论:
⠀⠀⠀首先,人们认为存在听觉、视觉、触觉和智力等不同的学习风格。这一观点最初由 Vester (1975) 在德国的研究背景下提出。
⠀⠀⠀其次,人们错误地推断,当学习者接受符合自己偏好的学习风格的信息时,学习效果会更好。
⠀⠀⠀最后,第三个被广泛传播但同样错误的结论是,教师必须判断学生的学习风格,并在教学中加以考虑。……然而,目前并没有实证研究能够证明,在教学中考虑学生学习风格的做法是有效的 (Willingham et al., 2015)。」
Kirschner & Hendrick 在其著作中(2024, pp.108)对此做出了精辟总结:
⠀⠀⠀「所谓的学习风格理论已经在一次又一次的研究中被证明是无稽之谈。实际上,并不存在所谓的『图像思考者』或『语言思考者』这样的区分。每个人都会运用图像和语言这两种思考系统,而且每个人都能从同时使用这两种系统中获得益处。你越是频繁地同时运用这两种系统,它们在你记忆中留下的印记就越深刻,你的记忆效果就越好,学习效果也就越好。」
| 工作记忆容量的差异很关键
然而,大脑有一个被广泛研究的属性,不仅存在个体差异,其差异还会影响个人的整体认知表现,这就是工作记忆容量。正如 Conway et al. (2007) 所阐述的:
⠀⠀⠀「工作记忆的一个基本特征是其容量有限,这直接制约了认知表现。因此,工作记忆容量较大的个体在各种认知任务中的表现通常优于容量较小的个体。
⠀⠀⠀例如,年长儿童的工作记忆容量通常大于年幼儿童;健康成年人的容量大于前额叶受损或患病的人;年轻成年人的容量又大于老年人。在所有这些情况下,工作记忆容量较大的个体在诸如复杂学习、阅读理解、听力理解和推理等多个重要的认知领域中,都表现出明显的优势。
⠀⠀⠀总之,研究证实了工作记忆容量确实存在个体差异,而且这种差异对日常认知表现具有重要影响。」
工作记忆容量的差异不仅体现在心理学层面,还体现在大脑活动的生理性测量指标中。Vogel & Machizawa(2004)的研究发现,当人们尝试执行达到或超过其工作记忆容量的任务时,大脑活动会达到一个饱和点。而工作记忆容量大的个体相对于工作记忆容量小的个体,达到这个饱和点的时间要晚得多:
⠀⠀⠀「我们的研究提供了人类大脑侧化活动的电生理学证据,这种活动反映了视觉记忆中信息的编码和维持过程。我们发现,这种活动的幅度与当前记忆中保持的物体数量密切相关。然而,当信息量达到或超过个体的存储容量时,活动幅度会逐渐趋于一个极限值。
⠀⠀⠀实际上,这个极限值精确地反映了每个个体的记忆容量。因此,低容量个体的大脑活动比高容量个体更快达到这个平稳状态。这种测量方法为我们提供了一个强有力的神经生理学预测指标,使我们能够直观地展示神经活动和记忆容量之间的直接关系。
⠀⠀⠀……
⠀⠀⠀换言之,我们只需测量应对不同规模的记忆任务时脑活动增加的幅度,就能准确预测一个人的记忆容量。」
Engström, Landtblom, & Karlsson (2013) 对这一现象提供了解释:个体的工作记忆容量越高,其大脑执行任务所需的神经活动就越少。换言之,对于工作记忆容量大的个体而言,相同的任务对他们的大脑造成的负担更小。
⠀⠀⠀「研究发现,随着任务难度的增加,无论是低容量还是高容量的参与者,其大脑活动都会相应增强。然而,两者之间存在一个关键差异:高容量参与者的大脑活动起始水平较低。」
> 工作记忆容量影响对自身努力程度的感知
因此不难理解,对于同一项任务,工作记忆容量较大的人通常会比容量较小的人感觉更容易完成。实际上,一项实验研究证实了这一点,该研究测量了人们在背景噪音中识别口语词汇的难度(Rudner et al., 2012):
⠀⠀⠀「……研究要求参与者在根据其语音识别能力调整的信噪比(即难度级别)下评估自身的努力程度。这样,在评估感知的努力程度时,就考虑到了语音识别能力上的个体差异;即便如此,工作记忆容量仍然能解释不同条件下对自身努力的感知的变化。
⠀⠀⠀……
⠀⠀⠀在相对有利的信噪比条件下,调制噪声和稳态噪声中感知听力努力的差异与工作记忆容量密切相关。……在所有三种难度级别和噪声类型中,相对于工作记忆容量较小的人,工作记忆容量较大的人都觉得在噪声环境中进行听力辨识更不费力。
⠀⠀⠀……
⠀⠀⠀听力难度的评分可能反映了工作记忆中显式处理资源的使用程度。因此,工作记忆和努力评级之间的关系可能表明,工作记忆容量较大的人在完成任务时所需的显式处理资源较少。」
> 工作记忆容量影响抽象能力
类似地,研究也表明,更高的工作记忆容量有助于提高抽象能力,即能够看见「由树木组成的森林」——通过学习潜在规则而非死记硬背具体细节来把握整体(McDaniel et al., 2014)。考虑到理解宏观模式需要在工作记忆中同时处理多个概念,这一发现并不令人意外。
⠀⠀⠀「……在完成函数学习任务的训练后,要么表现出掌握了训练中线索与标准关联的外推模式(即范例学习者),要么表现出能够抽象出函数规则的外推模式(即规则学习者;研究 1a 和 1b)。
⠀⠀⠀……
⠀⠀⠀研究 1c 和 2 进一步探讨了这些学习倾向在几个分类任务中的持久性。研究 1c 发现,与范例学习者(通过外推模式预先识别)相比,规则学习者在训练类别的泛化(迁移)过程中更倾向于避免使用特殊特征(即范例相似性)。研究 2 发现,在学习了抽象连贯类别后,规则学习者(而非范例学习者)在新的分类任务(迁移)中表现更佳。
⠀⠀⠀……
⠀⠀⠀研究发现,工作记忆容量(通过 Wiley et al., 2011 提出的 Ospan 方法测量)是预测个体在函数学习任务中倾向于依赖规则还是依赖范例的重要且独特的因素。具体而言,工作记忆容量越高,个体越倾向于依赖规则学习。
⠀⠀⠀更大的工作记忆容量可能通过多种方式促进学习过程中对函数规则的抽象,包括:
- 它使得个体能够同时保持和比较多个刺激(Craig & Lewandowsky, 2012);
- 它能够帮助个体将训练刺激分割为两个线性部分,并在学习过程中灵活切换(Erickson, 2008; Sewell & Lewandowsky, 2012);
- 它能够帮助个体克服或忽略初始偏见(例如,认为关系是正线性的),从而更准确地识别给定的函数关系(参见 Wiley et al., 2011)。
⠀⠀⠀因此,工作记忆容量较大的学习者可能更倾向于运用支持规则学习的认知过程(如关联多个训练试验、划分训练试验、忽略初始偏见等),而工作记忆容量较小的学习者则更难做到这一点。」
> 工作记忆容量影响学习速度
另一项研究发现,降低工作记忆容量会减缓解决谜题时的学习速度(Reber & Kotovsky, 1997):
⠀⠀⠀「研究结果显示,参与者首次尝试解决『球和盒子』谜题时,其表现受到了显著影响。具体来说,参与者解题速度的减慢程度与同时进行的次要任务所引起的工作记忆负荷增加程度成正比。然而,当参与者第二次面对同一谜题时,尽管谜题难度仍然较高,他们的表现却大幅提升。更值得注意的是,此时相同的工作记忆负荷不再影响他们解决问题的效率。这一发现表明,工作记忆容量减少的影响主要集中在首次解决谜题的过程中。换言之,学习如何解决谜题这一关键步骤,作为首次解题的核心内容,会被增加工作记忆负荷的次要任务所延缓。」
工作记忆容量对学习速度的影响并不局限于实验室环境中的解谜,它在现实生活中的学术研究和专业技能发展领域同样扮演着关键角色。一项针对钢琴演奏的研究有力地证实了这一点。研究发现,即使对于那些已经积累了数千小时练习经验的专业钢琴家而言,工作记忆容量仍然是预测其表现水平的重要因素。具体来说,相较于工作记忆容量较小的钢琴家,那些拥有较大工作记忆容量的钢琴家能够在较少的练习时间内达到相同的表现水平,或者在相同的练习时间内取得更为卓越的表现(Meinz & Hambrick, 2010)。
⠀⠀⠀「在对有着不同钢琴演奏水平(从初学者到专家)的参与者进行评估时,我们发现刻意练习可以解释钢琴视奏表现上占比近二分之一的差异。然而,工作记忆容量也展现出了正面的附加影响,而且没有证据表明刻意练习会减弱这种影响。研究表明,工作记忆容量具有普遍性、稳定性和遗传性特征,因此我们的研究结果对『专家级别的演出表现仅仅只是刻意练习的结果』这一观点提出了挑战。」
需要强调的是,虽然技能水平的差异主要可以通过有效练习的数量来解释,但工作记忆容量确实是一个不容忽视的重要的次要因素。正如 Kulasegaram, Grierson, & Norman (2013) 在其研究中总结道:
⠀⠀⠀「尽管所有研究都认同大量的刻意练习是形成专业技能的关键因素,但也有很多研究表明,即使在控制刻意练习的变量后,个体认知差异(如工作记忆容量)仍能预测专家表现的水平。这种影响的程度可能会因研究任务的性质和专家所运用的认知过程而有所不同。对于非常规或复杂的任务,工作记忆容量的重要性就显得尤为突出。」
在研究光谱的另一端,Swanson & Siegel (2011) 发现有学习障碍的学生的工作记忆容量通常较小:
⠀⠀⠀「我们认为,在阅读和/或数学领域,有学习障碍的个体的通用工作记忆容量比能够正常学习的同龄人要小,而且,这种容量不足的情况并不仅仅体现于他们在特定学科上的学习障碍(如阅读或数学)。……我们发现,在高认知负荷的情况下,与同年龄段的正常人相比,有学习障碍的个体在控制性注意力过程(例如,在面对干扰时,仍然对任务相关信息保持关注)方面存在缺陷。
⠀⠀⠀……
⠀⠀⠀实验研究得出的一个结论是,对于智力正常或高于平均水平的个体,工作记忆的个体差异(其中包括执行性处理问题的能力)与学业成就(如阅读理解能力)直接相关(Daneman & Carpenter, 1980)。因此,即使是智力正常的儿童或成人,在执行性处理问题方面也可能存在困难(或效率上的差异),这种困难并不仅限于智力低下的人群。
⠀⠀⠀……
⠀⠀⠀我们从近二十年的研究中得出结论,工作记忆不足是患有学习障碍的儿童和成人所面临的根本问题。此外,这些工作记忆问题与阅读障碍和数学障碍密切相关,可能还会影响写作能力。尽管工作记忆显然不是影响学业表现的唯一因素[例如,词汇和句法技能也很重要(Siegal and Ryan, 1988)],但工作记忆在解释学业成绩的个体差异方面确实扮演着关键角色。」
| 暂无证据表明工作记忆容量是可训练的
尽管我们可以通过训练提高在用于测量工作记忆容量的特定任务上的表现,但目前仍缺乏充分证据证明:这种进步能够真正提升工作记忆容量,并将其迁移到更广泛的场景中。Redick et al. (2015) 的研究对此有如下阐述:
⠀⠀⠀「虽然早期研究结果令人鼓舞,但对现有所有工作记忆训练效果证据的全面审视却不那么乐观。我们的结论是,工作记忆训练确实能在与训练项目高度相似的短期任务上带来一定的收益,但在提升学业成就方面,如阅读和算术能力方面,却并未显示出明显优势。
⠀⠀⠀……
⠀⠀⠀先前的研究表明,某些因素确实能提高个体在工作记忆测试中的得分(如重复测试、激励措施、策略指导等),但这种分数的提升未必反映了工作记忆能力的本质改变。举例来说,Ericsson et al. (1980) 的研究中,一名受试者通过记忆技巧成功地将数字连续回忆的数量提升到 79 个,然而在不涉及数字的其他记忆广度测试中,他的表现仍维持在正常水平(7±2)。
⠀⠀⠀……
⠀⠀⠀在经过严谨实验的大量研究中,几乎找不到支持『工作记忆训练能有效提升学业成就(如阅读、拼写和数学能力)』的证据。研究发现,工作记忆训练在较近的迁移任务上呈现积极效果,但在学业或成就测试的远迁移任务上却未见成效,这一发现与先前的元分析研究(Melby-Lervåg & Hulme, 2013; Rapport et al., 2013)结果一致。这表明,与普遍认知相反,工作记忆训练在教育领域的实际效益仍缺乏有力证据支持。」
然而,Anderson (1987) 提出了一个重要观点:通过训练特定领域的技能,可以有效地将长期记忆转化为工作记忆的延伸:
⠀⠀⠀「Chase and Ericsson (1982) 的研究表明,在特定领域积累的经验能够增加该领域的记忆容量。他们的分析揭示了这一现象的本质:随着新信息在长期记忆中的存储变得越来越可靠,长期记忆实际上成为了短期记忆的有效延伸。」
为了更好地阐明这一观点,我们直接引用 Chase and Ericsson (1982) 的原话:
⠀⠀⠀「我们在此强调的主要理论观点是:熟练掌握技能的一个关键要素,是能够快速访问存储在长期记忆中的、可直接检索位置的大量知识结构。我们认为,正是这些因素有效地增加了该知识领域的工作记忆容量。」
基于这些研究发现,自然可以理解Redick et al. (2015) 为何建议学生应该直接针对特定学科技能进行训练:
⠀⠀⠀「我们建议,相比于非结构化、无针对性的一般性干预措施(如认知训练和电子游戏训练),研究应该更多地聚焦于训练那些可能对特定学业成果产生近迁移效应的相似技能和能力。例如,针对阅读理解困难的儿童进行特定语言技能训练(Clarke, Snowling, Truelove, & Hulme, 2010),或者采用计算机辅助教学来提升阅读和数学技能(Rabiner, Murray, Skinner, & Malone, 2010)。」
这些建议与人类专业技能和表现领域最具影响力的研究者之一 K. Anders Ericsson 的观点不谋而合(Anderson et al., 1998):
⠀⠀⠀「长期以来,现代教育工作者一直致力于培养诸如创造力、通用问题解决方法和批判性思维等广泛适用的能力。然而,经过数十年的实验室研究和对人类认知结构的理论分析,人们开始质疑脱离特定知识和任务背景直接训练通用技能和认知过程的可行性。
⠀⠀⠀例如,关于思维和问题解决的研究表明,成功的表现高度依赖于特定的知识储备和已习得的技能。而学习和技能获得的相关研究也指出,个体表现的提升主要局限于特定领域的活动中。」
这些建议也得到了在数学学术干预研究领域拥有丰富经验的研究者 Amanda VanDerHeyden 和 Robin S. Codding (2020) 的支持:
⠀⠀⠀「元分析研究中总结和分析的证据表明:(a) 尽管认知测量与数学成绩存在相关性,但这些测量与学生对干预措施的反应并无关联;(b) 使用认知评估工具无法提供改善学术技能薄弱环节所需的信息;(c) 认知干预对改善学业表现几乎没有效果(Burns, 2016)。
⠀⠀⠀……
⠀⠀⠀[Jacob and Parkinson (2015)]的研究结论指出,很少有严谨的干预研究能够验证执行功能干预与学业成果之间的因果关系。……现有的研究显示,经过干预后,尽管学生的执行功能测量结果有所改善,但其学业成绩并未提高。因此,认为执行功能训练能提高数学能力的观点与现有证据不符。这些研究结果提醒我们,解决数学技能不足的最有效的方法是直接针对数学技能进行补习,而不是试图通过提高工作记忆或执行功能来解决数学技能的不足。」
| 不同学生需要的练习量各不相同
从以上讨论中,我们可以得出结论:一个有效的适应性学习系统应该聚焦于特定学科的学习任务,并根据观察到的学生实际学习速度进行调整,而非基于他们所谓的偏好学习风格。每个学生都需要获得足够的练习机会,以便在每项学习任务上达到精通水平——这个「足够」的练习量可能因学生个体和具体学习任务的不同而有所差异。
对于那些通常需要比他人更多练习的学生来说,这个事实可能令人稍感沮丧。但我们要再次强调本章前面引用的一项研究,该研究表明,一旦任务被学习到足够的熟练程度,工作记忆容量对任务表现的影响就会减弱(Reber & Kotovsky, 1997)。
⠀⠀⠀「研究结果显示,参与者首次尝试解决『球和盒子』谜题时,其表现受到了显著影响。具体来说,参与者解题速度的减慢程度与同时进行的次要任务所引起的工作记忆负荷增加程度成正比。有趣的是,当参与者第二次面对同一谜题时,尽管谜题难度仍然较高,他们的表现却大幅提升。更值得注意的是,此时相同的工作记忆负荷不再影响他们解决问题的效率。这一发现表明,工作记忆容量减少的影响主要集中在首次解决谜题的过程中。换言之,学习如何解决谜题这一关键步骤,作为首次解题的核心内容,会被增加工作记忆负荷的次要任务所延缓。」
更广泛地说,正如 Unsworth & Engle (2005) 所阐述的:
⠀⠀⠀「……工作记忆容量的个体差异主要体现在需要某种形式控制的任务中,而在那些只需相对自动化处理的任务中,差异几乎可以忽略不计。」
从这个角度来看,额外的练习不应被视为对学习速度较慢的学生进步的限制,而应被看作是一种赋能工具。它能帮助这些学生发展更强的自动性,从而减少认知差异对他们学习速度的影响,使他们能够继续学习更深入的内容。
我们强调,这完全符合成长型思维的理念,事实上,这是保持成长型思维的必要组成部分。没有人的当前知识水平是「固定的」或不可改变的。为了支持每个学生并最大化他们的学习效果,有必要为某些学生提供比其他人更多的练习机会。调整练习量以适应学生学习速度的个体差异,其根本目的是在最大程度上支持学生的成长。实际上,如果缺乏这种适应性,学生的成长必然会受到阻碍:
- 如果一个学生理解得较慢,而你没有给他们足够的练习机会,反而在他们尚未掌握当前内容就匆忙将他们推进到下一个阶段,那么你很快就会把他们推到远远超出他们能力的深度。结果是,他们只会一直挣扎,而不是真正学到东西,这无疑会阻碍他们的成长。
- 同样,如果一个学生很快就掌握了某个内容,而你却让他们练习的时间远远超过必要,而不是允许他们转向更具挑战性的材料,这也会阻碍他们的成长。
为了尽可能地支持每个学生在学习每项技能时的个人成长,Math Academy 为每个学生提供足够的练习以达到精通水平,并允许他们在掌握前置知识后立即转向更高级的技能学习。
你的数学潜力是有限的,但可能比你想象的更高。
迷思:每个人都能学会所有等级的数学。
现实:大多数人能够掌握基础数学,如算术和一些代数——但在此之上,更高等级的数学变得愈加抽象和技术化,只有少数人具备足够的认知能力来快速掌握并以此为职业,更不用说在他们人生的较早阶段就达到这一水平。
| 数学的等级
人们对数学难度的普遍误解存在这样一个问题:大多数人并不了解数学究竟有多少难度等级,也无法想象掌握最深奥数学知识所需的认知能力有多强。事实上,基础算术与研究生级别的数学之间存在天壤之别。虽然在普通人看来,微积分可能已经是「非常高深的数学」了,但实际上,微积分的难度还不及专业数学家所研究领域的一半。
为了帮助大家更好地理解这一点,我们粗略地将数学难度划分为以下几个等级:
- 算术 - 通常不被视为「难懂的数学」
- 代数 - 那些在学校时就不喜欢数学的人往往认为这已经很难了
- 微积分 - 在普通人眼中属于「高深莫测」的范畴
- 实分析、抽象代数、偏微分方程等 - 即使是数学专业的大学生也会觉得很有挑战性
- 代数拓扑、微分几何等 - 不仅研究生,就连许多数学教授都认为这些领域十分艰深
- 用于解决现代数学最著名问题的底层数学理论,例如证明庞加莱猜想所用的 Ricci Flow with Surgery - 这个等级的数学甚至会让世界顶级数学家都感到棘手
为了让大家更直观地理解这些数学等级的差异,我们可以借用运动领域的例子来做个形象的比喻:
- 学习算术就像学会基本的走路:几乎人人都能掌握。
- 学习高中微积分就像能够一口气跑完十英里:需要花时间和精力逐步提升,但只要训练方法得当并持之以恒,很多人最终都能做到。
- 而学习研究级数学则堪比获得奥运会 100 米短跑的参赛资格:这不仅需要先天的禀赋,还得投入数千小时进行最为艰苦的训练。
人们之所以更容易接受运动领域的这种差异,而对数学领域的差异感到难以理解,主要是因为我们无法像观察身体那样直观地看到大脑的构造和运作方式。然而,正如本章前面所讨论的,个体间的大脑差异确实存在(例如工作记忆容量的不同),而这些差异与关键的数学能力(如抽象思维能力)密切相关。
| 抽象能力的天花板
为了让「抽象能力」这个抽象概念变得更加具体,不妨听听著名学者 Douglas Hofstadter (2012)(译注:他的中文名:侯世达) 讲述他在攻读数学博士学位时,亲身体验到大脑中存在「抽象能力天花板」的经历:
⠀⠀⠀「毫无疑问,我是个『数学人』。从小就深深地爱上了数学,可以说我的一生都在思考数学相关的问题(一直持续到今天)。然而,在我二十多岁的时候,我突然意识到自己根本无法在足够抽象的层面上进行清晰思考,以至于无法为当代数学做出重大贡献。
⠀⠀⠀……
⠀⠀⠀我从未想过自己的头脑中会存在『抽象能力天花板』这样的东西。我一直理所当然地认为,随着知识的积累和数学经验的丰富,我理解数学抽象概念的能力会持续提升,就像在高中和大学时那样。
⠀⠀⠀……
⠀⠀⠀几年后,当我在数学研究生院学习时,我发现自己根本无法理解那些对成为一名优秀专业数学家至关重要的概念。或者说,即使我能理解,也是以极其缓慢的速度。即便如此,我的理解总是模糊不清,不得不经常回头复习,重新梳理那些微弱的理解。在那种高度抽象的层面上的内容……根本无法像本科阶段更具体的数学主题那样在我脑海中留下深刻印象……这感觉就像攀登高山,到了一定高度,空气变得如此稀薄,以至于人突然难以呼吸,甚至无法继续前进。
⠀⠀⠀……
⠀⠀⠀让我用一个更贴近生活的比喻来阐述:我就像一个在高中时叱咤风云的棒球明星,坚信自己必定会成为职业联盟的顶级球星。然而,现实往往事与愿违。几年后,他发现自己只能在某个默默无闻的小镇上的次级联赛中勉强算得上是个不错的球员,甚至从未有机会踏上大联盟的赛场。诚然,与普通人相比,他在棒球方面的天赋确实出类拔萃——或许是千里挑一,甚至万里挑一的水平——但与真正的职业球员相比,更不用说那些顶尖球星,他的能力还是相去甚远。
⠀⠀⠀……
⠀⠀⠀话说回来,我认为大多数人应该能够掌握一些基本的数学知识,比如分数的加减乘除、解线性和二次方程、基础的欧几里得几何等。他们甚至可能对函数有一定了解,对微积分的概念也有初步的认识。」
Hofstadter 所描述的「抽象天花板」并非一个「硬性」的门槛,让人突然失去进一步学习数学的能力。相反,它更像是一个「软性」的临界点:在达到这个水平后,学习数学所需的时间和精力会急剧增加,以至于继续深入学习高等数学不再是一个明智的选择。每个人的「抽象天花板」都不尽相同。对 Hofstadter 而言,这个天花板出现在研究生阶段的数学课程中;而对其他人来说,这个临界点可能出现得更早或更晚(但可以相当肯定的是,大多数人会比 Hofstadter 更早遇到这个瓶颈)。
| 学习投入与数学等级的关系
核心发现是,随着数学学习的深入,掌握更高等级知识所需的精力呈指数级增长。无论学习者是否意识到这一点,每个学习数学的人实际上都在经历一条能量投入(时间和努力)与数学等级之间的指数增长曲线。(指数曲线的一个重要特征是,它在初期可能看起来相对平缓,但在后期会呈现出急剧上升的趋势,尽管从一个点到下一个点的增长「倍数」是恒定的。)
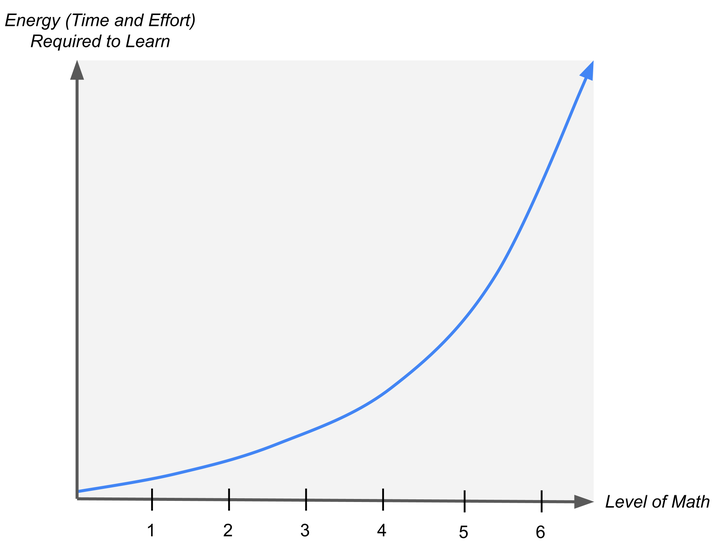
正如我们在本章前面所讨论的,工作记忆容量较小的人通常会感觉认知技能需要更多的努力和练习才能掌握。这就好像在学习所需的能量上乘了一个「倍数」。
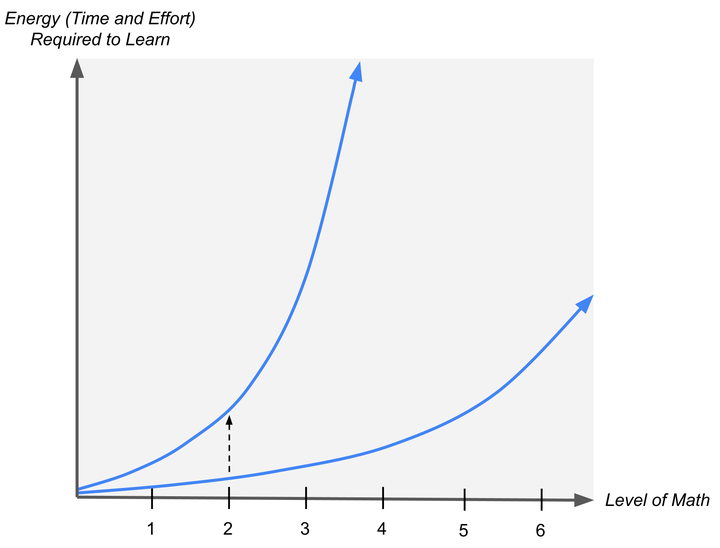
指数曲线的另一个关键特性是垂直缩放等效于水平平移。举个例子,如果我们把曲线 2^x 乘以 8(代表某人学习数学需要 8 倍的精力),那么得到的曲线 8 · 2^x 实际上等同于 2^(3+x),这相当于向左水平移动了 3 个等级。
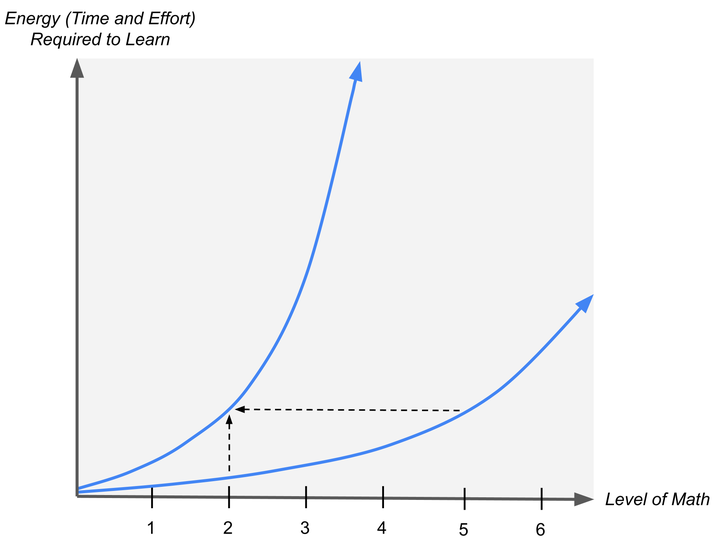
在初始阶段(图表左侧),两条曲线的差异并不明显,但随着我们视线向右移动(代表数学等级逐步提高),它们迅速分离,一条曲线比另一条更早呈现出急剧上升的趋势。每个人都处在这样一条曲线上,它反映了能量投入(学习所需的时间和努力)与抽象等级之间的指数关系,但每个人的曲线都会因其认知能力和学习动机/兴趣程度的不同而有所偏移。对某些人来说,数学直到研究生阶段的代数拓扑才变得具有挑战性;而对另一些人来说,高中代数就已经难以掌握了。
这些图表生动地说明了学习效率的重要性:通过提高学习效率,Math Academy 能够降低学习所需的精力投入,从而使上述曲线变得更平缓,这相当于将曲线向右移动。当学生处于高效的学习环境中,他们不仅进步更快,还能达到比其他情况下更高的数学等级。
一旦感觉学习效率过低,学生就会「跳下数学列车」,停止继续学习数学。当进步与付出的比率降得太低时,他们就会失去兴趣,转而投入其他进步-付出比更高的领域。保持高效率可以使进步与付出的比率尽可能高,让学生能在「数学学习列车」上走得更远,不断突破自己的数学能力极限。
| 人人可学一些,多数人可学更多,少数人可学全部
> 天赋还是努力?两者皆重要
这种观点与研究先天因素和后天环境对技能获取影响的常见结果相符:两者都至关重要。才能——即一个人在特定领域获取技能的最高速度——很重要,而努力同样不可或缺。正如 Kirschner & Hendrick 所述(2024, pp.142):
⠀⠀⠀「如果你试图让学生相信先天能力对成功的贡献为 0%,而努力对成功的贡献为 100%,那你就是在误导他们。我们不应该对学生说『天赋不重要,只有努力重要』,而应该告诉他们『是的,天赋和天生的能力在成功中扮演重要角色,但努力在边际效应上很重要,而这些边际收益可以累积成显著的进步』。」
缺乏天赋并不意味着「你无法做到」,但确实意味着相比有天赋的人,缺乏天赋的人需要付出更多努力,可能要达到难以企及的程度。然而,由于人类寿命有限,而个人天赋又如此多样化,「你需要比他人付出更多努力才能完成」实际上等同于「你可能不会去做,因为你会将时间用于其他更高效、更有成效和更能实现自我价值的事情。」
正如著名心理学家 Dean Keith Simonton 所总结的(2007):
⠀⠀⠀「……天赋这一概念并不意味着存在『达到卓越成就的先天限制』。相反,基因禀赋可能仅仅影响个体获取特定领域专长的速度,而不会对最终成就设置上限或下限。因此,实证研究表明,相比创造力较低的个体,杰出的创造性人才只是需要更少的时间来掌握必要的知识和技能(Simonton, 2000)。
⠀⠀⠀此外,在相同的专业知识水平下,天赋可能影响个体的表现水平。有天赋的人可能能从同等数量的陈述性和程序性知识中『获得更多收益』。但是,需要再次强调的是,这种增强效应并不等同于施加任何『先天限制』。」
在其他著作中,Simonton 进一步阐述(2013, pp.17-26)了先天和后天因素对专业表现发展的重要性。研究已经充分证实,专业水平的形成依赖于有利的社会文化环境、家庭和教育背景,以及大量的刻意练习:
⠀⠀⠀「环境因素在卓越成就的形成过程中扮演着关键角色。这些因素涵盖范围广泛,包括宏观的社会文化条件,以及更为直接的影响,如家庭背景和教育经历。……此外,在众多成就领域中,已经得到广泛认可的是,卓越成就与所谓的『刻意练习』密切相关(例如,Ericsson, Krampe, & Tesch-Römer, 1993; Krampe & Ericsson, 1996)。
⠀⠀⠀……
⠀⠀⠀如果这些关键环境因素中的任何一个完全缺失,无法为此提供任何支持,那么就无法成就卓越。举例来说,一个从不练习的小提琴手永远无法成为小提琴大师,甚至可能难以成为一个称职的业余演奏者。这一原则同样适用于社会文化因素。」
然而,研究表明,许多支撑专家级表现的关键特质实际上具有显著的遗传基础:
⠀⠀⠀「科研人员已经为多种关键的智力、性格倾向和身体特征估算出了相当精确的遗传系数(Bouchard, 2004; Bouchard, Lykken, McGue, Segal, & Tellegen, 1990)。研究发现,通常情况下,遗传因素至少能解释个体差异的三分之一,有时甚至超过一半。
⠀⠀⠀……
⠀⠀⠀这并不意味着所有能力或特质都具有显著的遗传性……只是那些没有显著遗传性的特质属于例外而非常规。可以肯定的是,大多数主要认知能力在很大程度上是遗传的,而与实现卓越成就相关的所有性格倾向特征也都表现出中等程度的遗传性。」
尽管专家级表现的形成依赖于有利的环境条件和大量的刻意练习,但遗传因素可以加速或减缓这一发展过程:
⠀⠀⠀「更为有效的定义角度是,从专业技能获取的角度来定义先天的才能(Simonton, 2008b)。这种定义将才能视为认知能力、性格特质和(在必要时)身体素质的综合。这些特质的全部或部分必须能够:(a)加快获取特定领域专业技能的速度(即『更快更好』效应),或(b)在相同的专业技能水平下提高特定领域的表现(即『事半功倍』效应)。可以说,先天禀赋是后天培养的催化剂和增强剂。
⠀⠀⠀……
⠀⠀⠀这一定义帮助我们解释了四个原本难以理解的现象。首先,不同个体在获得卓越所需专业技能的时间上存在巨大差异(Simonton, 2000)。其次,那些较快掌握专业技能的人通常比需要更长时间的人更有优势(Simonton, 2000)。第三,卓越往往与广泛的兴趣、多样化的爱好,甚至全面的才能有关(例如,Root-Bernstein, Bernstein, & Garnier, 1995; Root-Bernstein et al., 2008; Simonton, 1976; Sulloway, 1996)。如果每个领域都需要整整十年才能掌握足够的专业技能,那么任何人都不可能成为一个真正的博学者。最后,行为遗传学和差异心理学的实证研究已经明确识别出一系列能力和特质,这些特质不仅具有显著的遗传性,而且具有很强的预测效力(Bouchard & Lykken, 1999; Simonton, 2008b)。」
> 技能的习得速度很重要,因为时间有限
人类面临诸多现实约束,如有限的寿命,以及需要迅速掌握一项可以谋生的技能以获得能满足基本生活需求的工作。此外,各种事物总在争夺我们的注意力:每当我们觉得某事困难或乏味时,总有许多其他看似更容易且同样有趣的选择。因此,一旦我们在某个领域的进一步专业技能提升变得异常艰难时,我们往往会被其他方向所吸引。我们会转向那些我们认为能更好地利用有限时间的事物,而这种判断通常是正确的。
著名心理学家 Robert Sternberg 在 2014 年曾这样描述:
⠀⠀⠀「绝大多数想要成为专家的人——无论是小提琴家、滑雪运动员、物理学家还是其他领域的专家——最终都无法如愿。他们半途而废了。他们在尝试后发现,由于种种原因,这并不是适合他们的道路。我对此深有体会,因为当我从高中升入大学后,我发现自己作为一名大提琴手,已经无法在比高中时更激烈的竞争环境中立足。最终,我和许多人一样,决定将时间投入到其他更有价值的事情上。」
学习过程中还存在一些相互影响的因素:当我们在某个领域遇到困难并且表现不佳时,往往会对其失去兴趣和动力,这反过来又会使学习变得更加艰难。在我们年幼上学时,即使我们不情愿,教师或父母可能会强制我们继续投入精力学习数学等特定科目。然而,到了高中及以后,父母和教师对我们的学习投入和效果的监督就减少了。随着我们面临越来越多的生活责任,获得好成绩的压力也随之增加,这可能导致我们回避那些需要付出过多努力的课程。所有这些因素叠加在一起,当数学变得困难时,就会推动我们选择「退出」。
因此,从现实角度来看,「每个人都能掌握所有等级的数学并成为数学研究员」这种说法是完全不切实际的——就像并非人人都能成为奥运短跑选手、职业篮球运动员、举世闻名的喜剧演员或格莱美奖得主一样。但与此同时,几乎每个人都能学会基本的算术——就像几乎每个人都能学会跑步、投篮、讲笑话或哼唱一首歌。而且,通过适当的训练,大多数人都能学习一些代数知识——就像大多数人都能跑完 5 公里、投中三分球、逗乐观众或唱一首动听的歌曲一样。
| 为什么「每个人都能学会所有知识」的迷思长盛不衰
这个迷思之所以长盛不衰,至少有两个原因。首先,现实是「所有人都能学会一些,许多人能学会更多,但只有少数人能学会所有」,这可能让人感到不公平和不舒服——尤其是在数学领域,因为数学成绩最好的学生常常被视为最聪明的学生。
其次,人们往往高估了学习高等数学(以及其他技术性学科)对个人成功的重要性。实际上,许多工作,即便是那些备受尊重且收入丰厚的工作,并不需要高等数学。例如,有多少医生、律师、国会议员,甚至大学校长在工作中真正使用微积分?几乎没有。对于这些职业,高等数学并非必要。(尽管可能有比预期更多的从事这些职业的人曾学过高等数学,但高等数学知识本身通常不是他们能够获得并维持这些职业的关键因素。)
重要的是,所有人都应掌握基本的数学技能,而那些有数学天赋且对数学感兴趣的人——不仅是未来的数学家,还有未来的物理学家、生物信息学家、火箭科学家、机器学习工程师等——不应过早放弃,从而错失在自己热爱和擅长的领域建立职业生涯的机会。我们将在下一个迷思中更深入探讨这一观点。
作为揭穿当前迷思的最后一步,重要的是要认识到,即便是那些负责培训学生的专业教育者和教练,也可能倾向于推广这样一种观念,即任何人只要稍加努力就能做到任何事情。
教练们,像父母一样,往往不愿意告诉孩子,他们在某个领域没有足够的天赋或才华来将其作为职业——这是可以理解的,因为这样说不仅显得刻薄,而且可能并不准确:随着孩子的成长,新的和意想不到的天赋或才华可能会显现。
然而,对教练来说,尤其需要注意的是,还有其他激励因素在起作用。对他们而言,告诉学生的父母他们的孩子在某个领域没有足够的天赋或才华来从事相应职业,是没有好处的。这只会让父母和学生感到沮丧(尽管专业教练通常是正确的),而且在私人培训的背景下,往往会导致生意流失。因此,教练们倾向于去避免这种棘手的局面,转而采取以下错误立场之一:
- 天赋或才华无关紧要,任何人只要稍加努力就能做到任何事情。
- 天赋或才华很重要,但无法预测它们是否会在年轻学生成长过程中显现,因此基于此做出任何决定都是无意义的。
在揭穿当前迷思时,我们已经证明了第一种立场无法被理性地支持。然而,信奉这种立场会让人感到充满力量,进而显得非常有说服力,因此对于教练来说,这可能是一个有效的策略,可以让学生和家长感到满意。
同样,在第二种立场中,虽然即使是专业教练也无法绝对确定他们的学生(尤其是年轻学生)未来的发展方向,但他们通常确实掌握部分甚至许多的信息,关于如何判断学生是否具备天赋或才华——即使不知道这种信息,那他们也知道天赋或才华在孩子成长过程中出现的可能性有多大。利用这些信息可以在帮助孩子进入一个他们既有天赋又有兴趣的领域时发挥关键作用,从而最终建立他们所热爱的职业生涯。
| 艰难并不意味着无能
迷思:如果你在数学课上表现得很糟糕,这就意味着你无法学会这个等级的数学。
现实:如果你在数学课上表现得很糟糕,并不一定意味着你无法学会这个等级的数学。可能有多种原因导致你的艰难。虽然每个人的数学潜力确实有其上限,但我们所遇到的瓶颈往往并不代表我们真正的、如 Hofstadter 所描述的那种「抽象天花板」。各种因素可能会人为地降低我们的天花板,比如基础知识缺失、练习习惯不佳、无法或不愿意进行额外练习,或缺乏动力。
> 艰难可能源于基础知识的缺失
随着年龄的增长,人们会积累生物损伤,最终达到一个临界点,引发一连串的健康问题。学生在学习数学时也会出现类似的情况。
学生在数学学习中会积累弱点和知识缺口——即便成绩是 B+ 或 A-,也意味着课程中有些内容学生并未完全理解,更不用说掌握。此外,如果学生所学课程不够全面,未涵盖一些在高阶课程中被视为先验知识的主题,也会导致知识缺口。一旦学生积累了足够多的知识缺口(顺便说一句,一个缺口会引发更多缺口),那么除非采取适当的补救措施来填补这些缺口,否则学生将面临持续的困难。
Math Academy 自动采取措施来识别并修正每个学生的知识缺口。然而,若在自适应、自动化学习系统之外进行补救,则极为困难。在课堂环境中几乎不可能实现——因为教师没有足够的时间来逐一了解每个学生,找出他们具体缺失的基础知识。虽然有经验的导师可以进行补救,但通常需要长时间的多次辅导,以持续防止新的知识缺口的形成,这对大多数家庭来说费用过于昂贵。
学生通常在积累了大量知识缺口后就停止选修数学课程。通常的情况是,学生尝试按步骤模仿操作,而没有真正理解其中的原理,因为他们无法直观地领会所教授的新内容。不久之后,他们发现自己无法解决任何需要批判性思维或多步骤的问题。
这类似于职业运动员通常不是因为年纪太大而退役,而是因为积累了太多伤病。正如 Indiana Jones 所说:「不是年龄的问题,而是磨损。」或者如数学作家兼漫画家 Ben Orlin 幽默地描述的那样,这是「破沙发定律」:一个小小的缺失,随着时间的推移,会导致整个沙发变形,最终无法使用。
学生几乎可以肯定会在传统课堂中积累这些缺失。只有那些最有天赋和动力的学生才有能力和意愿自己识别并「自我修复」这些知识缺口。
- 在传统课堂上,学生常常在基础知识上遇到困难,但仍被要求完成更高难度的作业,这导致他们在没有真正理解内容的情况下「勉强应付」。
- 学生也不复习之前几年学过的内容,甚至通常不复习当前课程的内容,除非是在准备考试时。这导致他们很快遗忘所学知识,如果这些主题将来再次出现,他们需要从头开始重新学习。
然而,Math Academy 解决了这些问题,确保学生不会出现知识漏洞。
- 通过实行精熟学习,我们确保学生在掌握必要的前置知识之前,不会被要求学习更高级的主题。这样,学生始终能够充分吸收新学到的概念。
- 我们还采用间隔重复,这是一种系统的复习方式,通过在适当的时间间隔内复习已学内容,以保持知识的记忆。这样,学生不会遗忘所学内容。
- 我们的课程内容全面。在设计课程时,我们参考所有主要教材,以确保涵盖其所有内容。任何在某版本课程中可能出现的主题,你都能在我们的系统中找到。
即便学生带着知识漏洞进入 Math Academy,我们也会自动采取措施进行检测和修补。我们的诊断考试不仅评估课程内容,还评估低年级基础知识,以识别并填补每位学生的基础知识缺口。
> 艰难可能源于无效的练习
正如我们在总结学习科学时所解释的,有效的学习就像与私人教练一起锻炼。它应以刻意练习为核心,这是一种主动学习方式,通过重复和逐步改进,特别选择个性化的训练活动来提高特定表现。
我们将在后续章节中更深入地探讨主动学习和刻意练习,但以下是一些关键要点:
- 有效的学习是主动的,而非被动的。试图通过被动观看视频、听讲座、读书或重读笔记来学习并不有效。
- 刻意练习需要反复练习超出个人能力范围的技能。然而,这通常更费力且不那么愉快,可能会误导非专业人士
在他们的舒适区内进行练习。
- 有趣、协作且非重复的课堂活动(如小组讨论和自由形式/非结构化的项目或探索学习)有时可以提高学生的动机,缓解与刻意练习相关的不适感——但它们只是刻意练习的补充,而非替代。
- 刻意练习必须是持续例行的一部分。刻意练习的力量来自于长时间内逐步改进的累积效应。它不是一种像考前突击那样的「灵丹妙药」。
在 Math Academy,学生们通过解决新主题和最需要复习的主题的问题(并获得反馈)来进行刻意练习。我们将主动问题解决与教学交替进行,以便学生在使用信息积极解决问题并获得反馈之前,获取最低有效剂量的信息。
> 艰难可能源于练习不足
艰难可能是因为需要比其他学生更多的练习(或者,课堂进度可能太快)。这本身不一定是个严重问题,因为通常可以通过增加练习来解决。然而,如果与以下因素结合,可能会引发问题:
- 教学材料缺乏足够的框架支持。
- 练习题数量有限。
- 考试题目与作业题目差异较大。
- 额外练习的需求超过了你愿意为学习投入的努力。
Math Academy 解决了这些问题,除了最后一个:
- 我们的内容比其他地方的细化程度高约十倍。
- 如果学生在任务中遇到困难,我们会提供更多问题——即更多的学习和展示学习的机会。
- 我们有快速且频繁的小测验,问题与课程中学习的内容相似(但不完全相同)。
- 我们甚至为每位学生在每个主题上量身定制间隔重复的速度,以确保学生获得足够的复习来长期保留信息。
> 艰难可能源于缺乏动力
具有良好动机的学生通常受以下一个或多个因素驱动:
- 他们对学习内容有内在的兴趣。有些学生真正热爱数学,能在各种数学思想的结合中看到美,并因此获得新的视角。
- 学习内容与他们的未来目标高度相关。例如,一个有志成为火箭科学家的人可能不喜欢数学,但因为数学在将火箭送入太空方面的实用性而有动力去学习。同样,一个有志成为医生的人可能不喜欢数学,但在申请医学院时需要证明其具备基本的数学知识。即使是没有具体未来目标的学生,也可能希望保持潜在的职业机会,而这些机会可能因为数学学得不够而关闭。
- 他们喜欢参加数学竞赛和科学展览。有些学生对数学持中立态度,但发现自己擅长数学,并且喜欢学习更高级的数学以在考试和科学展览中获得竞争优势。
- 他们的父母通过有意义的外在奖励激励他们。有时,学生可能不属于上述任何类别,但他们的父母(通常是正确的)希望他们充分利用在校期间学习数学的机会。对于一些学生,这可能意味着学习生活所需的基础数学;对于其他学生,这可能意味着学习更高级的数学以打开各种职业机会。如果一个学生对其他活动如阅读小说、玩电子游戏,甚至只是出去吃甜点非常感兴趣,提供外在奖励以激励他们在数学学习中达到目标,通常可以提供足够的动力,以防止他们在学习过程中「退出」。
如果一个学生没有受到上述任何激励因素的驱动,他们可能会因为对学习内容缺乏兴趣而「退出」或感觉学习过程过于艰难。
| 类比寿命
本节的核心观点是:你的数学潜力虽有上限,但很可能超出你的想象。如果这个概念仍然不够清晰,不妨用人类寿命来作个类比。
你的生活方式会影响你的寿命,但即使你过着极其健康的生活,也不能保证你能活到超级百岁(110 岁以上)。极少数人能活到那个年纪,但即便你做对了所有事情,可能也不是你。然而,仍然可以肯定的是,如果你健康生活,你的寿命会比过着不健康生活时大大延长。
体育运动同样如此。即使你比其他人更长时间地进行有效练习,也不能保证你会成为名人堂运动员。然而,可以肯定的是,通过有效练习或投入更多时间,你会在所选运动中变得更加熟练。很可能,你会比自己或其他人认为的更为出色。
数学也不例外。即便你将一生投入到有效学习中,也不能保证你会成为世界级数学家。但通过认真努力地进行有效学习,你将学到更多数学,并打开更多职业机会的大门。
| 学生咀嚼量与课程颗粒度
在深入思考教学对学习者的支持作用时,人们可能会产生以下误解。
> 误解:如果教学做到完美,所有学生的学习速度会一样吗?
高等数学对智力的要求很高,这对许多学生构成了认知上的障碍。教学支架、指导和复习的目标是帮助学生跨越这些障碍。
然而,如果支架、指导和复习的目的是帮助学生克服认知障碍,那么在一个理想的学习环境中,拥有无限的支架、指导和复习是否会完全消除认知差异,使学生以相同速度学习?
的确,学生学习和记忆所学内容的速度因人而异。研究表明,有些学生学习速度更快、记忆维持时间更长,而其他学生学习速度较慢、遗忘得更快(例如,Kyllonen & Tirre, 1988; Zerr et al., 2018; McDermott & Zerr, 2019)。
但或许这些研究只是反映了不利的学习条件,而在一个理想的学习环境中,所有人会以相同的速度学习?
> 解答:在有利的学习条件下,学生的咀嚼量等于课程的颗粒度
继续深入思考这个思想实验,人们最终会意识到,无限的支架、指导和复习并不等同于最佳的有利学习条件。
的确,当喂给学生的每一勺信息都极其细小时,学生会以相似的速度吸收信息。然而,「以相同速度进食」会导致天花板效应。
学习速度较快的学生本可以更快地学习,但课程的颗粒度相对于他们的概括能力过细,或复习的频率相对于他们的遗忘速度过高,从而产生天花板效应,阻止快速学习者以最快速度学习。
一个最有利的学习环境要求课程的颗粒度与学生的咀嚼量相匹配,复习的频率与学生的遗忘速度相等。
修正后的比喻:当喂给学生的每一勺信息恰好和他们的咀嚼量相匹配时,学生会以相近的进食频率吸收信息。
这种学习环境将最大化每个学生的潜力,消除天花板效应。然而,关键是,学生不会以相同的速度进步:相同的进食频率并不意味着相同的食物摄入速度。
> 与观察现象一致
这种学习的有利条件的表述(「学生的咀嚼量等于课程的颗粒度」)与数学在不同等级上对于不同学生而言的变难程度不同的现象是一致的。在学生提升数学水平时,以下因素对他们的影响各不相同:
- 问题空间的组合爆炸——对于泛化能力较低的学生,会降低他们的「咀嚼量」,或者等同于细化课程的颗粒度。(这可能解释了为何有些学生在数学中表现良好,但在物理中遇到困难。)
- 需要维持记忆的大量知识——对于遗忘率较高的学生,增加了复习的需求。也减少了有效的「咀嚼量」,因为每次学习中越来越多的部分将用于复习模糊的前置材料。
这也与一个人在数学学习中所能达到的软性上限和硬性上限的概念相一致:
- 假设我们有一位泛化能力较弱且遗忘率较高的学生。对这样的学生来说,一个有利于学习的课程会需要更长的时间来完成(相较于普通学生),这是因为他们需要更细致的讲解和更频繁的复习,而且随着他们数学水平的提高,完成课程所需时间的倍数会不断增加。
- 在某个临界点上,「需要极大量练习才能学会」就变得等同于「无法学习」——首先是软性边界「投入如此大量练习所获得的收益,不足以弥补因此所忽视的、在其他更易掌握的领域去发展技能所带来的机会成本」,然后是硬性边界「所需的练习时间超过了个人余生所有清醒时间的总和」。
关键论文
注意:「重要性」部分可能包含了本章前文中直接引用的片段。如需引用本章内容,请以正文(上文)为准。
- Grospietsch, F., & Lins, I. (2021, July). Review on the prevalence and persistence of neuromyths in education–Where we stand and what Is still needed. In Frontiers in Education (Vol. 6, p. 665752). Frontiers Media SA.
Betts, K., Miller, M., Tokuhama-Espinosa, T., Shewokis, P. A., Anderson, A., Borja, C., ... & Dekker, S. (2019). International Report: Neuromyths and Evidence-Based Practices in Higher Education.Online Learning Consortium.
重要性:「学习风格」理论是教育领域最广为人知,同时也是被最全面地揭穿的神经迷思之一。这一理论认为,学习者在接收符合自己偏好的「学习风格」的内容时,学习效果会更好。 - Conway, A., Jarrold, C., Kane, M., Miyake, A., & Towse, J. (2007). Variation in Working Memory: An Introduction. In Conway, A., Jarrold, C., Kane, M., Miyake, A., & Towse, J. (Eds.), Variation in working memory (pp.3-17). Oxford University Press.
Vogel, E. K., & Machizawa, M. G. (2004). Neural activity predicts individual differences in visual working memory capacity.Nature, 428(6984), 748-751.
Engström, M., Landtblom, A. M., & Karlsson, T. (2013). Brain and effort: brain activation and effort-related working memory in healthy participants and patients with working memory deficits.Frontiers in human neuroscience, 7, 140.
重要性:大脑有一个被广泛研究的属性,不仅存在个体差异,其差异还会影响个人的整体认知表现,这就是工作记忆容量。工作记忆容量的差异不仅体现在心理学层面,还体现在大脑活动的生理性测量指标中。 - Rudner, M., Lunner, T., Behrens, T., Thorén, E. S., & Rönnberg, J. (2012). Working memory capacity may influence perceived effort during aided speech recognition in noise.Journal of the American Academy of Audiology, 23(08), 577-589.
重要性:对于同一项任务,工作记忆容量较大的人通常会比容量较小的人感觉更容易完成。 - McDaniel, M. A., Cahill, M. J., Robbins, M., & Wiener, C. (2014). Individual differences in learning and transfer: stable tendencies for learning exemplars versus abstracting rules.Journal of Experimental Psychology: General, 143(2), 668.
McDaniel, M. A., Cahill, M. J., Frey, R. F., Rauch, M., Doele, J., Ruvolo, D., & Daschbach, M. M. (2018). Individual differences in learning exemplars versus abstracting rules: Associations with exam performance in college science.Journal of Applied Research in Memory and Cognition, 7(2), 241-251.
重要性:更高的工作记忆容量有助于提高抽象能力,即能够看见「由树木组成的森林」——通过学习潜在规则而非死记硬背具体细节来把握整体。个体在抽象能力上的差异会对教育成果产生重要影响 - McDaniel, M. A., Cahill, M. J., Robbins, M., & Wiener, C. (2014). Individual differences in learning and transfer: stable tendencies for learning exemplars versus abstracting rules.Journal of Experimental Psychology: General, 143(2), 668.
Reber, P. J., & Kotovsky, K. (1997). Implicit learning in problem solving: The role of working memory capacity.Journal of Experimental Psychology: General, 126(2), 178.
Meinz, E. J., & Hambrick, D. Z. (2010). Deliberate practice is necessary but not sufficient to explain individual differences in piano sight-reading skill: The role of working memory capacity.Psychological science, 21(7), 914-919.
Kulasegaram, K. M., Grierson, L. E., & Norman, G. R. (2013). The roles of deliberate practice and innate ability in developing expertise: evidence and implications.Medical education, 47(10), 979-989.
Swanson, H. L., & Siegel, L. (2011). Learning disabilities as a working memory deficit.Experimental Psychology, 49(1), 5-28.
重要性:工作记忆容量会影响学习速度,即个体在接触、接受指导和练习某项任务的过程中,其执行该任务能力的提升速率。这种影响不仅存在于实验室环境中,还延伸到了学术和专业领域的真实生活场景中。 - Redick, T. S., Shipstead, Z., Wiemers, E. A., Melby-Lervåg, M., & Hulme, C. (2015). What’s working in working memory training? An educational perspective.Educational Psychology Review, 27(4), 617-633.
Reber, P. J., & Kotovsky, K. (1997). Implicit learning in problem solving: The role of working memory capacity.Journal of Experimental Psychology: General, 126(2), 178.
Unsworth, N., & Engle, R. W. (2005). Individual differences in working memory capacity and learning: Evidence from the serial reaction time task.Memory & cognition, 33(2), 213-220.
重要性:尽管我们可以通过训练提高在用于测量工作记忆容量的特定任务上的表现,但目前仍缺乏充分证据证明:这种进步能够真正提升工作记忆容量,并将其迁移到更广泛的场景中。然而,值得注意的是,一旦某项任务被学习到足够熟练的程度,工作记忆容量对该任务表现的影响就会减弱。对于那些已经达到自动化处理水平的任务,工作记忆容量的影响则微乎其微。 - Hofstadter, D., & Carter, K. (2012). Some Reflections on Mathematics from a Mathematical Non-mathematician.Mathematics in School, 41(5), 2-4.
重要性:随着数学学习的深入,掌握更高等级知识所需的精力呈指数级增长。这种现象导致了一种被称为「抽象天花板」的效应。这并非是一个「硬性」的门槛,让人突然失去进一步学习数学的能力。相反,它更像是一个「软性」的临界点:在达到这个水平后,学习数学所需的时间和精力会急剧增加,以至于继续深入学习高等数学不再是一个明智的选择。 - Simonton, D. K. (2007). Talent and expertise: The empirical evidence for genetic endowment.High Ability Studies, 18(1), 83-84.
Simonton, D. K. (2013). If innate talent doesn’t exist, where do the data disappear?.The complexity of greatness: Beyond talent or practice, 17-26.
重要性:研究已经充分证实,专业水平的形成依赖于有利的社会文化环境、家庭和教育背景,以及大量的刻意练习。然而,研究表明,许多支撑专家级表现的关键特质实际上具有显著的遗传基础。尽管专家级表现的形成依赖于有利的环境条件和大量的刻意练习,但遗传因素可以加速或减缓这一发展过程。缺乏天赋并不意味着「你无法做到」,但确实意味着相比有天赋的人,缺乏天赋的人需要付出更多努力,可能要达到难以企及的程度。
上一章:
下一章:
Thoughts Memo:第八章 有效练习的迷思与现实Thoughts Memo 汉化组译制
感谢主要译者 claude-3.5-sonnet,校对 Ravioli-T、Jarrett Ye
原文:The Math Academy Way: Using the Power of Science to Supercharge Student Learning
