小学过于看重计算能力有必要吗?

熟练的计算能力对于进一步学习数学是必要的。但具体怎么培养计算能力、何时培养计算能力，就是另外一个问题了。

以下内容摘自 @Thoughts Memo 汉化组的译文《第十五章 培养自动性》

⠀⠀⠀摘要：自动性是指无需有意识的努力就能执行低层次技能的能力。就像篮球运动员能在轻松运球的同时能够制定比赛战术一样，自动性可以使人们能够不在低层次任务上浪费有限的认知资源，而是将这些资源用于更高层次的思考任务。如此可见，自动性成为了通向专业、创造力和整体学术成功之路的门户。然而，基础技能的自动性不足会增加任务的认知负担，进而使学生在学习和表现时面临极大困难。

自动性的重要性

| 自动性解放工作记忆

减少认知负荷的一个关键但常常被忽视的部分就是培养基础技能的自动性，即无需有意识努力就能执行那些低级技能的能力。自动性之所以重要，是因为它能释放有限的工作记忆，使其可以并行处理多个低级技能，并基于这些低级技能进行更高层次的思考。

以一个熟悉的例子来说，想想篮球运动员需要同时实现的所有技能：他们需要跑动、运球，同时还要思考战术。如果他们必须有意识地思考跑步和运球的动作，他们就无法同时做到这两点，并也没有足够的脑力来思考比赛战术。

这同样适用于学术领域。正如 Hattie & Yates (2013, pp.53-58) 所描述的：

⠀⠀⠀「如果你的思维能量被低层次的处理占据，你就无法掌握『全局』。阅读的连续性被打破，目标从理解整体内容转变为仅仅理解眼前的字词。……如果你阅读连贯的文本（如句子）的速度低于每分钟 60 字，那么理解你所读的内容几乎是不可能的。

⠀⠀⠀……

⠀⠀⠀许多学生在入学时缺乏基本的声音-符号功能的自动性。即使通过基本的语音训练，他们可能能够识别字母，理解声音与符号的关系，并通过极大努力可以阅读单个单词。但如果不通过密集的自主练习来提高处理速度，那么实现理解性阅读仍然遥不可及。

⠀⠀⠀……

⠀⠀⠀经充分验证发现，在小学低年级结束之前表现出数学学习困难的学生，通常在快速、自动化调用数学基本知识的能力上存在明显不足。这种能力欠缺不仅会阻碍学生在数学上的进步，还往往会引发一系列负面影响，例如丧失自信心、对学习失去兴趣，甚至产生无助感。」

| 工作记忆是有限的，但长期记忆是无限的

不幸的是，工作记忆的容量非常有限，大多数人只能同时在脑海中保留少量新信息（涵盖大约 7 位数字，或广义上逻辑连贯的 4 个组块），且由于记忆会因自然衰退或干扰而减弱，所以只能维持大约 20 秒，（Miller, 1956; Cowan, 2001; Brown, 1958; Ricker, Vergauwe, & Cowan, 2016）。更何况，这还是在不需要对这些信息进行任何认知处理的情况下——如果需要进行认知处理，那么由于有限的处理资源会被分散，就会导致能够记住的内容会变得更少（Wright, 1981）。工作记忆在处理新信息时的这种严重限制被称为变化窄限原则（Sweller, Ayres, & Kalyuga, 2011）。

一个简单直观的类比可以帮助我们理解工作记忆的限制：想象一下，你的双手是如何限制你抓握和操作物品的。你可能可以同时拿着手机、钱包、钥匙、铅笔、笔记本和水瓶——但你无法再多拿其他东西。如果你想做某些事情，比如发短信、在笔记本上写字或打开水瓶盖，那你可能需要先放下几样物品。

我们的工作记忆有着类似的限制，它只能同时处理大约 7 个新的信息单元。一旦这些位置被占满，如果我们想要记住更多信息或处理已有的信息，就必须清空一些空间来腾出位置。

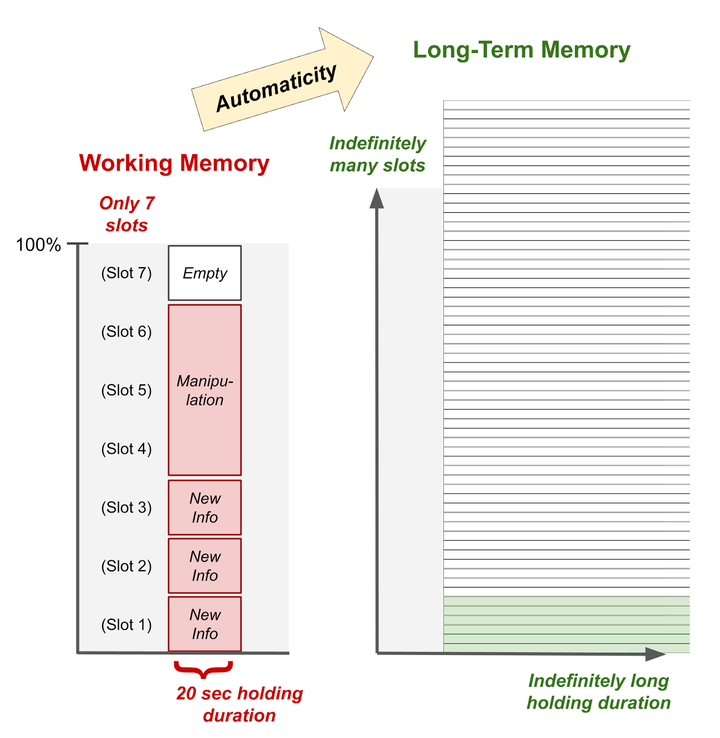
值得注意的是，如果我们无法在工作记忆中同时容纳问题的所有要素，就无法解决这个问题。这意味着，如果学生还没有将基础技能变成自动化的操作，那么即使教师再怎么精心设计新技能的认知支架，学生也无法掌握。研究表明，即使是在学生认知能力范围内的任务，过重的认知负荷也会显著增加出错的可能性（Ayres, 2001）。

然而，当我们将某项技能或知识点转化为自动化操作时，我们就可以运用它而不占用工作记忆的空间。相反，这项技能会被储存在长期记忆中。在长期记忆里，我们可以无限期地存储无数信息，而不需要额外的认知努力。

正如 Anderson（1987）所总结的，自动性能够有效地将长期记忆转变为短期记忆的延伸：

⠀⠀⠀「Chase 和 Ericsson（1982）的研究表明，在某个领域积累的经验可以增加该领域的认知容量。他们的分析揭示，这种现象的本质是新信息在长期记忆中的存储变得极其可靠，以至于长期记忆实际上成为了短期记忆的有效延伸。」

为了更好地阐明这一点，我们直接引用 Chase 和 Ericsson（1982）的原话：

⠀⠀⠀「我们在这里想要强调的主要观点是，熟练表现的一个重要组成部分是能够快速访问存储在长期记忆中可直接检索位置的大量知识结构。我们认为，这些因素实际上增加了该知识库的工作记忆容量。」

| 专业技能需要自动性

自动性是区分专家和新手的关键能力，这一现象已在多个领域得到深入研究，其中国际象棋是一个典型例子。Ross（2006）对此做出了精辟的总结：

⠀⠀⠀「……一位典型的国际象棋大师能够掌握约 50,000 到 100,000 个棋局信息组块[Gobet & Simon, 1998]。大师只需瞥见棋局，就能从记忆中迅速调用这些信息组块，这就像大多数英语母语者听到开头几个词就能脱口而出『玛丽有只小羊羔』这首童谣一样自然。」

Gobet & Simon（1998）进一步阐释道：

⠀⠀⠀「……下棋的技能主要依赖于两个方面：（a）在对弈过程中识别棋局中的熟悉模式，以及（b）探索可能的走法并评估其后果。……专家的记忆能力包含了在长期记忆中缓慢形成的结构（如检索结构和模板），这些结构通过可变的『插槽』增强了短期记忆，使得专家能够迅速将当前棋局的信息填充其中。」

事实上，Benjamin Bloom（1986）在研究才能培养时将自动性视为一个关键因素，他指出早在 19 世纪，自动性就被形象地比喻为「天才的手脚」：

⠀⠀⠀「我们在才能培养领域的研究印证了 Bryan 和 Harter 1899 年关于专业摩尔斯电码报务员自动性培养的研究。他们极为精辟地阐述了自动性作为学习成果的益处。

⠀⠀⠀『学习者必须能够用一次专注完成现在需要六次专注才能完成的任务，进而用一次更全面的专注完成现在需要三十六次专注的任务。他必须系统化自己的工作流程，并培养与之相应的自动化习惯体系。当他做到这一点时，他就在自己的[职业或专业]领域中掌握了主动权。最终，他的整套习惯体系将能迅速应对并解决新问题。自动性本身并不等同于天才，但它是天才施展才能的得力助手。』」

重要的是要认识到，自动性远不止简单的熟悉。如果你真正「掌握」了某项知识，那么你应该能够快速而准确地调用和运用这些信息。如果做不到这点，那么你只是对它「有所了解」而已。在学习层次性知识体系时——无论是数学、国际象棋、运动还是乐器——真正掌握知识而不仅仅是熟悉它们至关重要。为什么？因为你无法在仅仅熟悉的基础上继续建构知识。这就是所谓「基础不牢」的含义。你只能在坚实的知识基础上继续前进。

为了帮助学生培养自动性（从而在数学领域获得专业水平），Math Academy 要求学生反复练习每项技能，直到他们达到足够的掌握程度。学生从他们的知识边界（而非「熟悉」的边界）开始学习，在完全掌握前置知识之前不会被推进到下一个学习阶段。此外，为了帮助将已掌握的技能巩固到长期记忆中，这些技能会通过一种称为间隔重复的系统方法（将在本文档后面详细介绍）在未来持续复习。

案例研究：比较有无乘法和加法自动性对指数计算的影响

为了充分说明自动性的重要性，我们不妨通过一个案例研究来观察不同自动化水平的学生是如何解决同一个问题的。通过这个案例，我们将会看到，学生的整体学习体验可能会因为其自动性的不同而产生巨大差异。

假设我们有三位学生——Otto、Rica 和 Finn，他们的名字代表了各自的自动化水平。

• Otto 已经完全自动化了乘法口诀和运算过程。
• Rica 还不熟悉乘法口诀，每次都要重新计算。她能够进行乘法运算，但不够熟练，需要慢慢来，并写下每一个步骤。
• Finn 和 Rica 一样不熟悉乘法口诀，而且连加法也不熟练，所以他什么都要用手指数。他对乘法运算完全不熟悉。

这三位学生都上了一堂关于数的立方的课。在老师解释了什么是数的立方，并用一个例子演示之后，每人都收到一道练习题：计算 4^3。让我们来观察每位学生解决这个问题时的思维过程（包括推理和情感反应）。

Otto 对乘法和加法非常熟练，他在 10 秒内就在脑中解决了这个问题。他觉得这很容易，迫不及待地想要尝试下一题，甚至期待更具挑战性的问题，比如计算负数、小数和分数的立方。

• 4^3 就是 4 × 4 × 4。4 × 4 = 16，这个简单，然后 16 × 4 嘛……10 × 4 = 40，6 × 4 = 24，加起来就是 40 + 24 = 64。搞定，太简单了！下一题是什么？

Rica 用了 2 分钟解决了这个问题，但答案不对。她又花了 2 分钟纠正错误，但已经感到疲惫，想在继续下一题之前休息一下。她对接下来可能遇到的更难的问题感到有些担忧。

• 4^3 等于 4 × 4 × 4。4 × 4 是多少来着？我得算一下。
• 4 × 4 就是 4 + 4 + 4 + 4，也就是……嗯，4 + 4 = 8，再加 4 是 12，再加 4 是 16。
• 我刚才算到哪儿了？哦对，4 × 4 = 16，然后还要算 16 × 4……唉，又得用那个乘法步骤了。
• 把 16 写在上面，下面乘 4，然后按步骤来。先算 4 × 6 = 6 + 6 + 6 + 6，数一下是 6 + 6 = 12，加 6 是 18，再加 6 是 22。写下 2，进 2。然后 4 × 1 = 4，加上进位的 2，写下 6。
• 好了。结果是 62。哎呀，老师说接近了但不太对。行吧，再算一遍。
• （Rica 重复了上述整个过程，这次得到了 64。）
• 太好了，老师说 64 是对的。我知道还有更多题要做，但这一题就有点难了，我有点累了。老师，我能休息一下再做下一题吗？

Finn 花了 10 分钟解这道题，但答案不对。他又试了 10 分钟，但犯了另一个错误。老师不得不陪着他又花了 10 分钟帮他完成这道题。等 Finn 终于搞定这道题时，差不多一节课都过去了。他筋疲力尽，感到无比沮丧，对剩下的作业充满恐惧。

• 4^3 就是 4 × 4 × 4。4 × 4 等于多少？不知道，得算一下。
• 4 × 4 就是 4 + 4 + 4 + 4，这个……唉，得全部数出来。真烦人。
• 从 4 开始，再加 4 是 5、6、7、8。
• 从 8 开始，再加 4 是 9、10、11、12。
• 从 12 开始，再加 4 是 12、13、14、15。
• 呼，算了好久，现在得到 4 + 4 + 4 + 4 = 15。我刚才为什么要算这个来着？哦对了，我是在算 4 × 4 = 15。
• 等等，还没完呢。我算出了 4 × 4 = 15，但我其实是要算 4 × 4 × 4。好吧，现在还得算 15 × 4。天啊，这个更难了。我真不想做。但没办法，继续吧。
• 15 × 4 就是 15 + 15 + 15 + 15，这些数字太大了，得在纸上排好才行。
• 把 15 写在最上面，下面再写一个 15，再下面一个 15，最后一个 15。
• 现在加右边那一列：
• 从 5 开始，再加 5 是 6、7、8、9、10。
• 从 10 开始，再加 5 是 10、11、12、13、14。
• 从 14 开始，再加 5 是 15、16、17、18、19。
• 写下 9，进 1，然后加左边那列：从 1 开始，再加 1 是 2，再加 1 是 3，再加 1 是 4，再加 1 是 5。写下 5，我们得到 59。
• 答案是 59。终于算完了。花了好长时间。哎呀，老师说不对。别吧……难道我得重来一遍吗？！这也太累人了。
• （Finn 又重复了一遍上述过程，这次得到了 66，还是不对。他明显变得很沮丧，老师只好坐下来和他一起检查。他们找出并纠正了几处错误，最后得到了正确答案 64。）
• 我今天实在做不动了。太累了。我讨厌数学，老师给的作业太多了。而且下一题看起来更难，作业上还有那么多题！太糟糕了。快下课了，我就等着铃响吧。

这个案例研究清楚地表明，学生在基础技能上的自动性越高：

• 他们就越容易掌握新的高级技能，
• 他们就能更快速、更独立地运用这些技能，
• 他们对整个学习过程的感受就越积极，
• 他们就越有兴趣继续学习更深入的内容。

总的来说，培养出自动性的学生会感到自信有力；而没有培养出自动性的学生则会感到不知所措和沮丧。

自动性、创造力与高阶思维

| 自动性是创造力的必要前提

人们常常误解自动性和创造力之间的关系。有种观点认为， 这两者是对立且相互排斥的：自动性需要不断重复练习， 会将学生变成毫无思想的机器， 而要充分发挥人类创造力， 就必须摆脱这种机械化的思维模式。这种论调乍一听似乎很有说服力， 甚至颇为便利， 因为学生通常不喜欢为了培养自动性所需的重复练习。然而， 这种观点存在一个致命的错误。

事实上， 自动性是创造力不可或缺的基础。自动性的根本目的是减少大脑在机械性任务上的资源消耗， 从而释放认知资源， 用于更高层次的思考活动。如果学生没有养成自动性， 就必须有意识地思考每一个低级别的行为， 这会耗尽他们的认知容量， 最终导致无暇进行高层次的创造性思考。

以写作这一普遍被视为最具创造性的活动为例。高效的写作需要一个从头脑构思到纸上成文的畅通无阻的过程。如果作者需要有意识地考虑拼写、语法、词义、句子间的过渡以及段落划分等基本问题， 他们就会陷入低层次的机械性任务中， 无法腾出精力去关注高层次的创造性细节， 如生动的意象、逻辑的连贯性， 以及不同表达方式和创意所能唤起的情感共鸣。

事实上，写作教育领域的研究者已经证实了自动性的重要性(Kellogg & Whiteford, 2009)：

⠀⠀⠀「严肃而有效的写作不仅是对记忆力、语言和思维能力的严峻考验……更取决于写作者能否妥善应对写作任务对工作记忆提出的繁重要求。

⠀⠀⠀……

⠀⠀⠀如果不能降低计划、构思和审阅这些过程对工作记忆的相对需求，必要的协调和控制能力就无法成功实现。当任何单一过程消耗过多可用资源时，写作者就无法灵活且适应性地协调计划、构思和审阅这些环节。如果写作者还在为处理各个部分而苦苦挣扎时，那么他就无法顾及作品的整体。」

更重要的是，这一观点得到了过去至少半个世纪大量研究的支持：

⠀⠀⠀「大量实证研究有力地证明了工作记忆资源，尤其是执行注意力在高级写作技能发展中的重要性。首先，研究发现，大学生的整体工作记忆容量与其写作表现呈现显著相关（Ransdell & Levy, 1996）。Vanderberg 和 Swanson（2007）进一步发现，高二年级学生写作技能的个体差异可以通过中央执行能力的差异来解释。在解释个体技能差异时，受控的执行注意力比信息的储存更为关键。相关实验结果表明，当用记忆六位数字的任务分散执行注意力时，会同时降低文本写作的质量和流畅度（Ransdell, Levy, & Kellogg, 2002）。

⠀⠀⠀写作技能从初级到高级的提升，取决于充足的工作记忆资源，以及恰当分配这些资源于规划、句子生成和复查的能力。McCutchen（1996）回顾了大量支持这一观点的证据。例如，在儿童完全掌握手写和拼写的基础技能之前，他们生成书面文本的流畅度是有限的（Graham, Berninger, Abbott, & Whitaker, 1997）。在小学阶段，将这些写作的机械技能练到自动化是必要的，这样才能释放工作记忆用于规划、生成和复查等更高级的写作任务。此外，掌握手写和拼写也是写作者开始培养认知、情感和行为控制能力的必要条件，这些能力对青少年持续产出文本至关重要（Graham & Harris, 2000）。

⠀⠀⠀对于正在发展中的写作者来说，由于工作记忆的限制，修改能力往往受到限制，甚至可能完全缺失。修改需要检测问题、诊断原因，并找到合适的纠正方法（Flower et al., 1986）。如果修改失败的原因是由于工作记忆限制，而非缺乏对修改内容的认知，那么提供提示来检测文本问题应该会有所帮助，因为写作者可以将认知资源集中用于诊断和解决问题。事实上，研究表明提供提示确实能改善包括大学生在内的写作者的修改能力（Hacker, Plumb, Butterfield, Quathamer, & Heineken, 1994）。

⠀⠀⠀正如Beal（1996）所观察到的，非常年轻的写作者甚至难以理解他们文本的字面意思。初学写作者往往过度专注于自己的想法，从而忽视了文本本身的表达效果。在儿童期和青春期早期，在工作记忆中维持写作者的想法就已经占用了大部分甚至全部的的可用存储和处理能力。这阻碍了学生仔细阅读自己的文本，并形成一个清晰的、独立于作者意图的文本表示。」

| 自动性：高层次思维的基石

这一原理同样适用于数学学习。如果想要达到更高层次的数学思维和抽象思考能力，就必须先在基础层面上培养自动性。一位校长从质疑到认同的经历很好地说明了这一点（Brown, Roediger, & McDaniel, 2014, pp.44-45）：

⠀⠀⠀「关于 Roger Chamberlain 校长最初对哥伦比亚中学练习测验的担忧——担心这可能只是一种包装精美的死记硬背方法，我们在研究结束后向他询问。他思考片刻后回答道：

⠀⠀⠀『我现在真正理解并认同的是：如果想要让学生能够在不同情境下评估、综合和应用某个概念，那么他们首先需要具有扎实的知识基础和良好的记忆力。这样，他们就不会浪费时间去回想某个词的含义或某个概念的内容。而这种基础能力会使他们更容易达到更高的思维层次。』」

Lehtinen et al. (2017) 直截了当地指出：

⠀⠀⠀「基本算术运算和数字组合技能的熟练程度对后续数学学习至关重要，而这些技能的自动性不足是数学学习障碍儿童的典型特征。」

Allen-Lyall (2018) 进一步解释道：

⠀⠀⠀「内化的事实知识能够促进高效的心算，这使得解决多步骤问题或认识并建立各种数学概念之间的联系变得更加容易，比如乘法和除法、比率比较、分数等价以及几何中的图形关系探索等（Chapin & Johnson, 2006; National Research Council, 2005）。

⠀⠀⠀……

⠀⠀⠀当一个人内化了乘法口诀，在执行需要更复杂或连续算术操作的任务时就能节省脑力（Geary, 1999; Geary, Saults, Liu, & Hoard, 2000）。当不需要通过反复加法或查看表格来计算乘积时，数学概念之间的灵活思考和概念性跳跃就成为可能（Royer, 2003）。因子和乘积之间的关系成为探索更具挑战性数学的起点。如果每次面对新的数学问题都要回归到将乘法视为重复加法或依赖视觉辅助，可能会阻碍直觉性数学思维的形成（Goswami, 2008）。

⠀⠀⠀如果工作记忆需要大量资源来确定两个数的乘积或某个乘积的因子，流畅的心算就会受到阻碍。通过记忆基本数学事实可以减轻认知负担，使工作记忆能够更好地分配资源来处理更复杂数学问题所需的数字关系（Goswami, 2008; LeFevre, DeStefano, Coleman & Shanahan, 2005）。」

| 自动性：数学素养和学业成功的门槛

Allen-Lyall（2018）从更宏观的角度阐释了数学基本运算的自动性如何成为数学素养的门槛，进而影响未来的学业和职业发展：

⠀⠀⠀「当一个人对自己的数学思维充满自信并能展示扎实的能力时，他不仅能在学校数学表现中脱颖而出，还能获得更广泛的大学学习和就业机会（Atweh & Clarkson, 2001; Marsh & Hau, 2004; Valero, 2004; Williams & Williams, 2010）。

⠀⠀⠀由于众多原因，基本运算的熟练掌握成为了通往真正数学素养的教育门槛。因此，在这个充满各种需要数学交流想法的挑战的世界里，帮助儿童掌握这个看似微小但至关重要的早期数学学习要素变得尤为重要（D'Ambrosio & D'Ambrosio, 1994; Thomas, 2001）。」

其他研究人员的发现，自动性对学业成就的影响会立即显现：在基本数学运算上反应较慢的学生，一旦接触多位数运算就开始落后于反应更快的同龄人（Joy Cumming & Elkins, 2010）。

⠀⠀⠀「研究者根据儿童在基本运算包上的反应时间将他们分类。反应最慢的群组在许多运算包上仍使用计数策略；最快的群组则使用检索或高效思考策略。群组类别成为预测多位数任务表现的最佳指标。加法运算的准确性仅对不需进位的任务有影响，而年级水平的影响并不显著。对错误类型分析显示，多位数加法中的大多数错误源于基本运算的不准确，而非算法错误。这表明，基本运算的低效解决方案增加了认知负担，使得多位数运算变得难以处理。」

回顾过去，将自动性和创造力对立起来的观点不仅在事实上是错误的，而且颇具讽刺意味。那些错误观点暗示，减少重复练习可以促进创造力，从而有利于未来的成功。然而实际上，这种做法导致学生不得不持续将精力花在本可以通过重复练习而自动化完成的低层次任务上，从而限制了他们进行更高层次和创造性数学思维的能力，甚至限制他们未来的学业和职业发展前景。

自动性的神经科学机制

从神经生理学角度来看，自动性的形成涉及到大脑中策略性神经连接的发展。这些连接能够降低大脑激活特定神经元模式所需的能量消耗。

研究人员通过功能性磁共振成像（fMRI）观察到了这一现象（Shamloo & Helie, 2016）。他们对比了参与者在执行自动化和非自动化任务时的大脑活动。研究发现，当人们处于清醒但放松的状态，且不是在专注于需要注意力的任务时，大脑中被称为默认模式网络（DMN）的区域会保持一定水平的活动。DMN 体现了人们的背景思维过程。有趣的是，那些已经形成自动性的人能够在不打断这些背景思维的情况下完成任务：

⠀⠀⠀「DMN 是一个相互连接的脑区网络，当人们不专注于外部任务时保持活跃，而在需要集中注意力的任务中被抑制……在自动化阶段（不同于分类学习的早期阶段），参与者在接收刺激后无需中断他们的背景思维过程：他们可以继续『走神』，同时仍能出色地完成任务。」

当外部任务需要高度集中时，它会抑制 DMN：DMN 的活动减弱，因为大脑需要将更多资源分配给与任务相关的特定区域。然而，当大脑对某项任务形成自动性后，DMN 与任务相关区域之间的连接会增强，执行任务时对 DMN 的抑制程度也会随之降低：

⠀⠀⠀「……某些 DMN 区域在初始训练阶段会被抑制，但在形成自动性后则不会。大量练习后，DMN 的抑制程度显著降低。

⠀⠀⠀……

⠀⠀⠀研究结果显示，在形成自动性后，DMN 与其他脑区（包括非 DMN 区域）的功能连接增强，而内侧前额叶皮层和腹内侧眶额皮层之间的功能连接减弱。这些发现进一步支持了自动分类中策略转变的假说，并将自动性的认知概念和神经科学概念联系起来，表明自动处理过程中对认知资源需求的减少伴随着 DMN 的去抑制以及 DMN 与任务相关脑区之间更强的功能连接。」

简而言之，自动性的实现依赖于形成更高效的神经连接网络。这些连接减少了大脑执行特定任务所需的努力，从而使大脑能够同时为背景思维过程分配更多资源。这一发现不仅揭示了自动性的神经生理基础，还为理解学习过程和认知资源分配提供了新的视角。

关键论文

注意：「重要性」部分可能包含了本章前文中直接引用的片段。如需引用本章内容，请以正文（上文）为准。

• Miller, G. A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information.Psychological review, 63(2), 81.
  Cowan, N. (2001). The magical number 4 in short-term memory: A reconsideration of mental storage capacity.Behavioral and brain sciences, 24(1), 87-114.
  
  重要性：人类的工作记忆的容量非常有限，大多数人只能同时在脑海中保留少量新信息：大约 7 位数字，或广义上逻辑连贯的 4 个组块
  
  
• Ayres, P. L. (2001). Systematic mathematical errors and cognitive load.Contemporary Educational Psychology, 26(2), 227-248.
  
  重要性：即使是在学生认知能力范围内的任务，过重的认知负荷也会显著增加出错的可能性
  
  
• Ross, P. E. (2006). The expert mind.Scientific American, 295(2), 64-71.
  
  重要性：一位典型的国际象棋大师能够掌握约 50,000 到 100,000 个棋局信息组块。大师只需瞥见棋局，就能从记忆中迅速调用这些信息组块，这就像大多数英语母语者听到开头几个词就能脱口而出「玛丽有只小羊羔」这首童谣一样自然。
  
  
• Gobet, F., & Simon, H. A. (1998). Expert chess memory: Revisiting the chunking hypothesis.Memory, 6(3), 225-255.
  
  重要性：下棋的技能主要依赖于两个方面：（a）在对弈过程中识别棋局中的熟悉模式，以及（b）探索可能的走法并评估其后果。专家的记忆能力包含了在长期记忆中缓慢形成的结构（如检索结构和模板），这些结构通过可变的「插槽」增强了短期记忆，使得专家能够迅速将当前棋局的信息填充其中。
  
  
• Bloom, B. S. (1986). Automaticity: "The Hands and Feet of Genius." Educational leadership, 43(5), 70-77.
  
  重要性：Benjamin Bloom 在研究才能培养时将自动性视为一个关键因素，并指出早在 19 世纪，自动性就被形象地比喻为「天才的手脚」
  
  
• Kellogg, R. T., & Whiteford, A. P. (2009). Training advanced writing skills: The case for deliberate practice.Educational Psychologist, 44(4), 250-266.
  
  重要性：在写作领域，自动性的重要性得到了至少过去半个世纪大量研究的支持。严肃、有效的写作对工作记忆提出了繁重的要求。为了释放工作记忆用于规划、生成和复查等更高级的写作任务，学生必须在小学阶段将这些写作的机械技能练到自动化。如果写作者还在为处理各个部分而苦苦挣扎时，那么他就无法顾及作品的整体。
  
  
• Allen-Lyall, B. (2018). Helping students to automatize multiplication facts: A pilot study.International Electronic Journal of Elementary Education, 10(4), 391-396.
  
  重要性：基本运算的熟练掌握成为了通往真正数学素养的教育门槛。内化的事实知识能够促进高效的心算，这使得解决多步骤问题或认识并建立各种数学概念之间的联系变得更加容易。通过记忆基本数学事实可以减轻认知负担，使工作记忆能够更好地分配资源来处理更复杂数学问题所需的数字关系。
  
  
• Joy Cumming, J., & Elkins, J. (1999). Lack of automaticity in the basic addition facts as a characteristic of arithmetic learning problems and instructional needs.Mathematical Cognition, 5(2), 149-180.
  
  重要性：自动性对学业成就的影响会立即显现：在基本数学运算上反应较慢的学生，一旦接触多位数运算就开始落后于反应更快的同龄人
  
  
• Shamloo, F., & Helie, S. (2016). Changes in default mode network as automaticity develops in a categorization task.Behavioural Brain Research, 313, 324-333.
  
  重要性：自动性的实现依赖于形成更高效的神经连接网络。这些连接减少了大脑执行特定任务所需的努力，从而使大脑能够同时为背景思维过程分配更多资源。

上一章：

下一章：

Thoughts Memo 汉化组译制
感谢主要译者 Jarrett Ye，校对白侑
原文：The Math Academy Way: Using the Power of Science to Supercharge Student Learning

相关专栏

← 返回目录