@天下 提到的精熟学习法确实是经过实证研究,可以提高应试成绩。但是这种学习方法和传统教学格格不入,难以在没有技术介入的情况下推广。
精熟学习法的内涵非常简单:如果没有掌握某个知识的前置知识,就不要学习这个知识,直到其前置知识被掌握为止。
以下内容摘自 @Thoughts Memo 汉化组的译文《第十三章 精熟学习》
⠀⠀⠀摘要:Math Academy 将课程组织为知识图谱,从而可以精准追踪主题间的前置关系,进而能够实现精熟学习。精熟学习要求学生在学习新主题之前必须熟练掌握前置知识。尽管非常粗略的精熟学习方法都能显著提升学生的学习效果,但这种方法与传统教学格格不入,且提高了对老师的教学要求,因而难以普及。Math Academy 实现了更细致的精熟学习,这需要针对学生进行定制化教学,而这只能通过一对一教学来实现。
精熟学习未被充分利用
我们的主要教学方法之一是精熟学习,它同样由 Bloom 提出。精熟学习要求学生在学习更高级的主题之前必须熟练掌握前置知识。真正细致的精熟学习需要完全定制化的教学,而这只能通过一对一教学来实现。
有一些办法能让教师大体上实现精熟学习,比如 Bloom 的为精熟而学习策略(Learning For Mastery, LFM),和 Keller 的个性化教学系统(Personalized System of Instruction, PSI)。Kulik, Kulik, & Bangert-Drowns (1990) 总结道:
⠀⠀⠀「采用 LFM 和 PSI 的课程中,需要学习的材料被划分成了一系列简短的单元,学生会参与阶段性单元测试,评估自己对每个单元的掌握程度 (Bloom, 1968; Keller, 1968)……其中LFM 课程中的单元是由老师提供的,学生按照老师掌握的统一节奏推进学习。而PSI 课程中的单元主要以书面材料体现,学生按照自己的节奏推进学习。」
然而,Bloom 在描述两个标准差问题时也发现了,一个教授 30 个学生的老师,如果执行精熟学习,那么学习效果提升的效应量是 1 个标准差(一对一辅导有 2 个标准差)。尽管大量研究都证实了非常粗略的精熟学习(由一个老师手动管理)能得到非常显著的学习效果,但大部分研究没能复现所谓 1 个标准差的强度(平均的效应量是 0.5 个标准差) (Kulik, Kulik, & Bangert-Drowns, 1990):
⠀⠀⠀「数据显示精熟学习方法对学生学习效果有积极作用。在大学,高中和小学高年级中,这种方法平均能将期末考试成绩提升 0.5 个标准差左右,或者将学生水平从 50% 提升到 70% 。 尽管 PSI 和 LFM 策略有一些地方有所不同,并且对两种教学方法的研究差异也非常大,但针对 PSI 和 LFM 的研究的结果都有类似的提升。PSI 对考试成绩有平均 0.48 标准差的提升;LFM 对考试成绩有平均 0.59 标准差的提升。」
遗憾的是,尽管精熟学习(甚至是粗略的)在课堂中已被充分证明能提升学习效果,但其并没有被广泛采用,原因在于它既偏离了传统教学范式,又需要教师和管理者付出更多努力(Sherman, 1992)。(的确有一小部分老师在尝试某种差异化教学,但这和真正的精熟学习并不一样,真正的精熟学习对所有学生一视同仁,其教学也是完全个性化的)
John Gilmmour Sherman (1992) 是 Keller 的个性化教学系统(PSI)的共创者,研究者,实践者,他悲叹道:
⠀⠀⠀「有些 PSI 课程虽然很成功,但是被禁止了。我知道有些同事收到了禁令。有些人是研究中大名鼎鼎的人物,他们的课程是有效的,有客观数据为证。
⠀⠀⠀我也有这种经历。为了避免正面冲突,乔治亚镇大学的心理系主任宣布,对于 50% 左右的课堂时间必须用来教学。如此一来,自主安排的可能性便几乎归零,那么有效 PSI 课程也更无从说起了。
⠀⠀⠀他发布这条规定,是因为对于课堂来说『是课堂中智力的迸发才能启迪学生』。但没有数据支持这点!自以为是捍卫学术,但又武断地评估教学方法的好处,这种行为太过不妥。
⠀⠀⠀这些案例令人忧心的地方在于:这些决策完全没有数据支持。对教育过程的研究究竟有没有用,我们甚至要怀疑这点,令人忧心。」
Buskist, Cush, & DeGrandpre (1991) 写到,类似 PSI 的精熟学习方法被禁止,是因为这些方法威胁了传统教育机构:
⠀⠀⠀「任何机构的头等大事都是延续自身的存在。一旦目标设立,就必须维持现状,如果可能的话,去前进改观。如果目标没有实现,那么机构自然命悬一线。PSI 的潜在后果会威胁教育机构的延续和教育机构守护者的地位,根据 Keller 所言,
⠀⠀⠀『如果类似 PSI 的系统得到官方认可,在教育系统从上到下展开应用……每个学生都自己安排学习,那么什么时候要开始正式教育呢?对于上课时间,大学,学期,学年又会如何呢?而谁能获得奖学金和那些奖品?谁又可以成为优等生荣誉学会(Phi Beta Kappa)?谁又会成为班级毕业致辞代表?……如果课程学习长度改变,那么学费的支付又该怎么改变?课程学习的计划又该如何定义?』
⠀⠀⠀换句话说,教育改革最大的阻碍就是教育系统本身。这就是为什么,本世纪所有重大教育改革,最终都被引到了改革课纲上,而没有改变教师如何教学(参考Skinner, 1984; McGovern, 1990)。
⠀⠀⠀改革课纲不需要对教育机构动刀子。因为课纲虽然有些变化,但也到此为止了。课还是一堂堂,一学期一学期地上。成绩分布仍然要拟合正态分布,学生在上更进一步的课程前也并不需要掌握基础知识。学生仍然需要花上四年来完成高等教育的要求。
⠀⠀⠀Keller 的计划与这套策略完全相反。他想要大刀阔斧地改革教学。在一个完全基于 PSI 的学校里,学生可能在两年就能学完大学课程,甚至更早,学得更多。设想整个教育系统都是基于 PSI 的:大批仍处于青春期的人将会从大学毕业。这对许多教育者而言是不安的。由此可见,PSI 将对教育系统及其拥护者产生威胁。
⠀⠀⠀PSI 在我们的现代教育系统中没有容身之地。基于课堂教学的悠久传统积累已久,难以根除。为了自我延续,教育机构只会支持改革教学的内容,而非教学方法本身。」
实现精熟学习
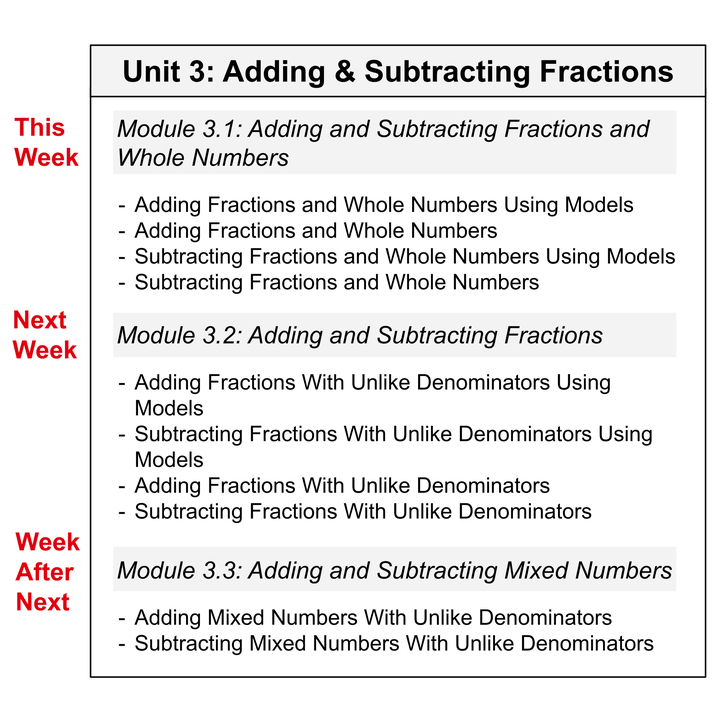
在传统教学方法中,老师会牵着学生,按照一个提前决定的课程计划(比如下图所示的计划),线性地学习一系列概念。但如果学生没有跟上节奏,不理解某个地方,老师也通常只会让他继续学习新主题,尽管新主题的前置概念并没有掌握。长此以往,学生在课堂上收获会越来越小,甚至会开始厌恶数学。
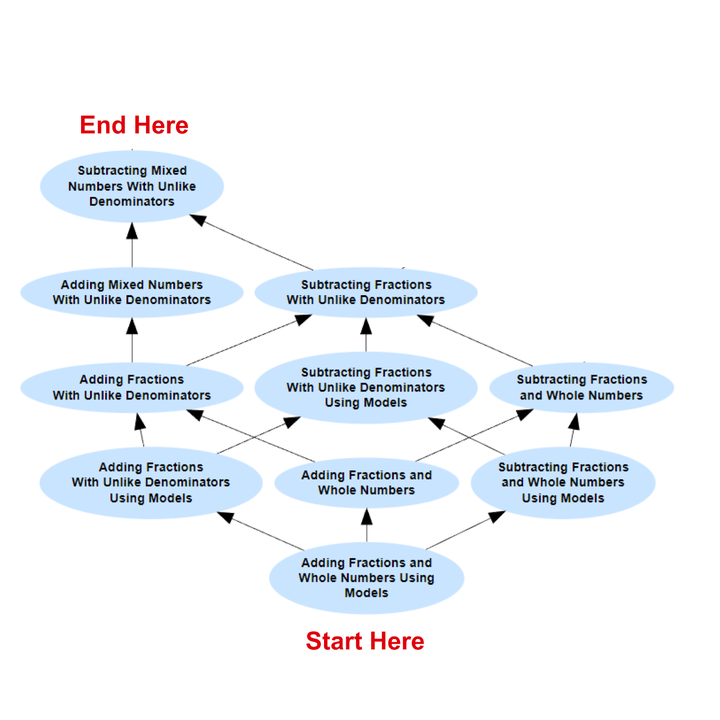
Math Academy 则精细地实现了真正的精熟学习。我们将知识组织成知识图谱,描述了所有主题和他们之间的前置知识关系。在下面的知识图谱中,箭头从简单的前置知识指向更高级的「后继」知识。
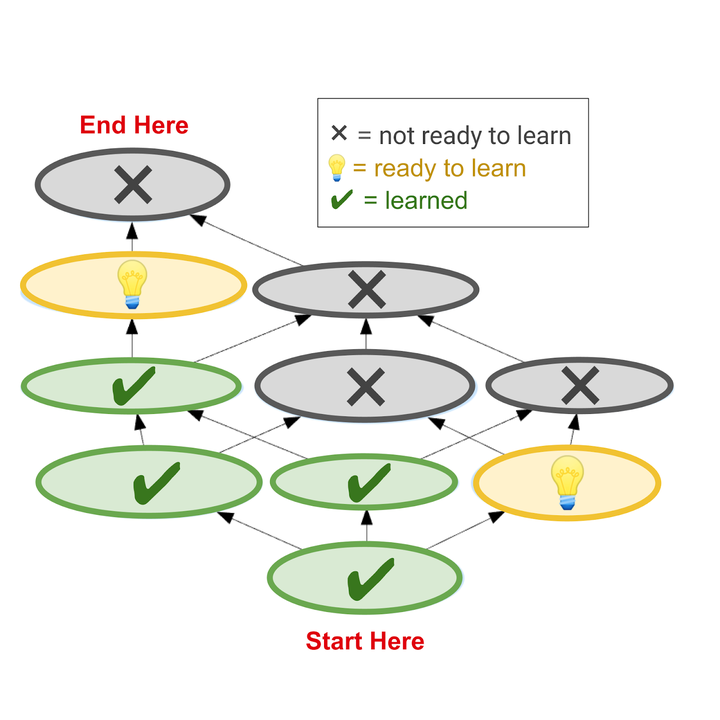
将学生的进度叠加到图谱上,我们便能识别出他们能学习的主题——也就是前置知识已经充分掌握的主题。我们只让学生学习这些主题相关的课程。如果学生某些主题上遇到阻碍,他们可以改天再尝试解决,并且与此同时,他们可以学习其他新的课题,只要这些新主题与遇到阻碍的主题关联不大。
老师一次只能教授一个主题,所以单靠一个老师,是不可能为一整个班级的同学手动实现真正的精熟学习的,毕竟班级里每个学生的学习情况都不相同。况且研究者发现,即便是同一年级的学生,他们的知识档案都存在巨大差异 (Pedersen, et al., 2023):
⠀⠀⠀「根据我们的结果,四年级和八年级的学生中,分别有 38% 和 49% 的学生或是理解本年级的内容有困难,或者已经掌握的这些内容了。」
然而,Math Academy 完全自动化的可交互课程能够支撑非同步式学习,同一时间内不同学生会学习不同课程。利用一套模拟了高级教师决策的软件系统,我们能大规模提供完全自动化的教学,并实现了真正的细致精熟学习。
知识前沿是最近发展区
精熟学习和 Vygotsky 的近侧发展区的理论紧密相关。近侧发展区(Zone of Proximal Development)指的是有些任务是学生在他人支持的情况下能完成,但靠自己完不成的。学生完成这种任务是学习效果最好。
对于自适应学习系统来说,学生的最近发展区和他们的知识前沿或者是精熟边界是重合的,也就是他们掌握了前置知识但还没学习的主题。学生学习位于知识前沿的学习任务能够取得飞速的学习进步。
比如说,另外一个学习平台报告(Zou et al. 2019),即使老师根据学生的成绩数据按自己理解主观选择适合全班学生学习的新主题,如果该主题位于学生的知识边界内,那么学生掌握该主题的成功率会比学习超出知识边界主题提高 3 到 4 倍。由此,作者总结道:
⠀⠀⠀「……单纯把数据提供给老师,是不足以做出好的教学决策的。为了优化学习成果,需要根据学生的近侧发展区(ZPD),做出合适的教学决策,引导学生走上合适的个性化之路。」
可以用知识档案的边界来可视化学生的知识边界,这能大概描述学生的数学大脑的发达程度。每当学生学习新的数学主题时,就像他们脑中长出了新的脑细胞,并和已有的脑细胞相连。一开始,新的脑细胞很弱小,需要时常照顾,但慢慢地细胞就会茁壮成长,不需要频繁打理了。
比如,下图是第二学期微积分学生的知识档案。已学习的主题被涂上阴影(阴影越深,练习完成得越好),主题之间的箭头表示前置关系。
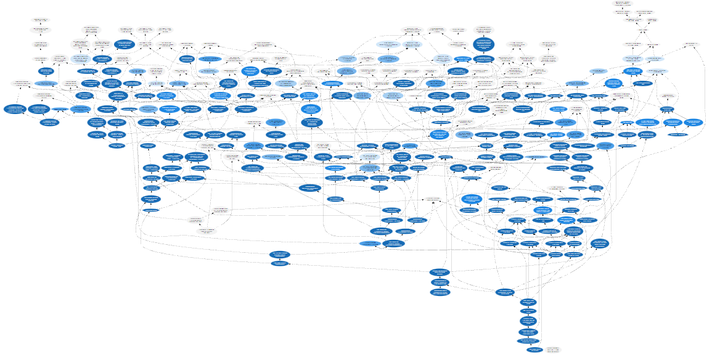
(注意这个可视化仅仅展示了学生整个数学大脑的一个「子系统」——微积分课程里有数百个主题,但 Math Academy 的整个数学培养方案里有数千个主题,从小学数学到大学数学都有覆盖)
知识边界是知识档案的边界,划分了学生掌握与未掌握的界限。
- 学生掌握了知识边界之下的所有简单主题。他们掌握了这些主题的前置知识,前置知识的前置知识,以此类推。
- 然而,他们并未掌握在知识边界以及之外的高级主题。
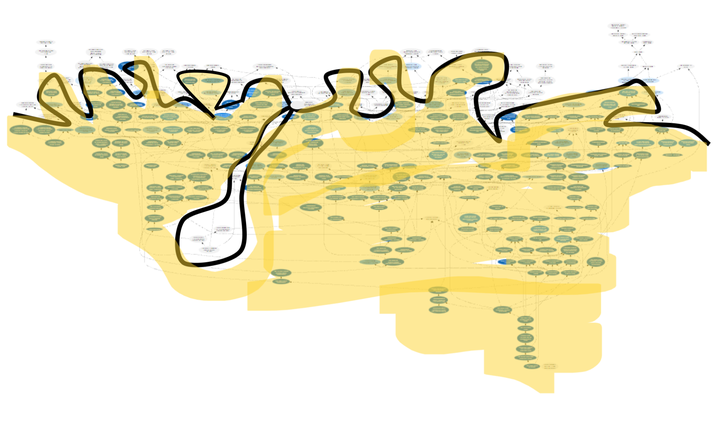
当学生刚开始使用 Math Academy 时,我们会进行诊断性测试,这是一个动态评估,能够快速估计他们知识边界。根据诊断结果,只要给学生提供新课程,这些课程总是针对我们估计的学生知识边界的主题,而随着学生完成这些课程,知识边界的估计也会越来越准确。
关键论文
注意:「重要性」部分可能包含了本章前文中直接引用的片段。如需引用本章内容,请以正文(上文)为准。
- Bloom, B. S. (1984). The 2 sigma problem: The search for methods of group instruction as effective as one-to-one tutoring.Educational researcher, 13(6), 4-16.
重要性:接受一对一辅导的学生平均表现超过了传统班级 98% 的学生,其效应量达到了两个标准差的水平。然而,一个教授 30 个学生的老师,如果执行精熟学习,那么学习效果提升的效应量只有 1 个标准差。 - Kulik, C. L. C., Kulik, J. A., & Bangert-Drowns, R. L. (1990). Effectiveness of mastery learning programs: A meta-analysis.Review of educational research, 60(2), 265-299.
重要性:尽管大量研究都证实了非常粗略的精熟学习(由一个老师手动管理)能得到非常显著的学习效果,但大部分研究没能复现所谓 1 个标准差的强度(平均的效应量是 0.5 个标准差) - Sherman, J. G. (1992). Reflections on PSI: Good news and bad.Journal of Applied Behavior Analysis, 25(1), 59.
Buskist, W., Cush, D., & DeGrandpre, R. J. (1991). The life and times of PSI.Journal of Behavioral Education, 1, 215-234.
重要性:尽管 Keller 的个性化教学系统(一种能让教师大体上实现精熟学习的方法)在课堂中已被充分证明能提升学习效果,但其并没有被广泛采用,原因在于它既偏离了传统教学范式,又需要教师和管理者付出更多努力 - Pedersen, B., Makel, M. C., Rambo-Hernandez, K. E., Peters, S. J., & Plucker, J. (2023). Most mathematics classrooms contain wide-ranging achievement levels.Gifted Child Quarterly, 67(3), 220-234.
重要性:即便是同一年级的学生,他们的知识档案都存在巨大差异:四年级和八年级的学生中,分别有 38% 和 49% 的学生或是理解本年级的内容有困难,或者已经掌握的这些内容了。 - Zou, X., Ma, W., Ma, Z., & Baker, R. S. (2019). Towards helping teachers select optimal content for students. In Artificial Intelligence in Education: 20th International Conference, AIED 2019, Chicago, IL, USA, June 25-29, 2019, Proceedings, Part II 20 (pp. 413-417). Springer International Publishing.
重要性:另外一个学习平台报告,即使老师根据学生的成绩数据按自己理解主观选择适合全班学生学习的新主题,如果该主题位于学生的知识边界内,那么学生掌握该主题的成功率会比学习超出知识边界主题提高 3 到 4 倍。
上一章:
Thoughts Memo:第十二章 刻意练习
下一章:
Thoughts Memo 汉化组译制
感谢主要译者 Jarrett Ye,校对白侑
原文:The Math Academy Way: Using the Power of Science to Supercharge Student Learning
