注: 本章将展开阐述第十八章[1]和第二十二章[2]中介绍的概念。
⠀⠀⠀摘要: 我们提出了理论最大学习效率这一概念,它可以类比于物理学中光速不可超越的现象。对于给定的知识图谱 ,其最大学习效率取决于知识点间的包含密度——然而,知识图谱无需完全被包含,甚至不需要接近完全包含状态,其最大学习效率就能接近理论极限。Math Academy 的数学知识图谱包含了足够多的知识点包含关系,使其最大学习效率接近理论极限。在实践中,学生个体所能达到的实际学习效率主要取决于其学习表现的质量,其次(在较小程度上)才受其学习速度(即每日平均完成的学习量)的影响。
什么是学习效率?
| 理论最大学习效率
在物理学中,没有任何物体的速度能超过光速。这是任何物理物体可以达到的理论最大速度,一个宇宙常数。
在间隔重复的背景中,存在一个类似的概念:理论最大学习效率。 理论上,如果给定一个知识点间充分相互关联的知识体系,学习者就有可能在不显式复习先前已学内容的情况下,完成所有间隔重复任务。
举一个简单的例子:设想有一系列主题,它们之间层层包含——第一个主题的知识完全被第二个主题包含,第二个主题又被第三个主题包含,以此类推。
每当你学习一个新主题时,所有下层相关主题都会自动获得完整的隐式复习。假设你总有新主题可学,那么你需要进行显式复习的唯一原因是当你多次尝试学习下一个主题却屡屡失败。
重要的是要认识到,一个知识图谱不需要完全或几乎完全由包含关系构成,其最大学习效率就能接近理论极限。即使主题间的大多数关系不是包含性的,只要有一定比例的包含关系存在,也能产生显著效果。
以 Math Academy 的数学知识图谱为例,它包含了足够的包含关系,使其最大学习效率接近理论极限。我们通过实际观察发现,在实践中,大多数数学课程平均每个主题只需约一次显式复习就能掌握。理论上,一位在每项学习任务中都表现完美的优秀学生,甚至需要的显式复习更少。
| 理论最小学习效率
相对而言,还存在理论最小学习效率的概念。这正是独立抽认卡的场景——或者等同于一组没有任何包含关系的主题集合。
在这种情况下,任何主题都无法从其他主题获得隐式复习。每一次复习都必须显式地进行。
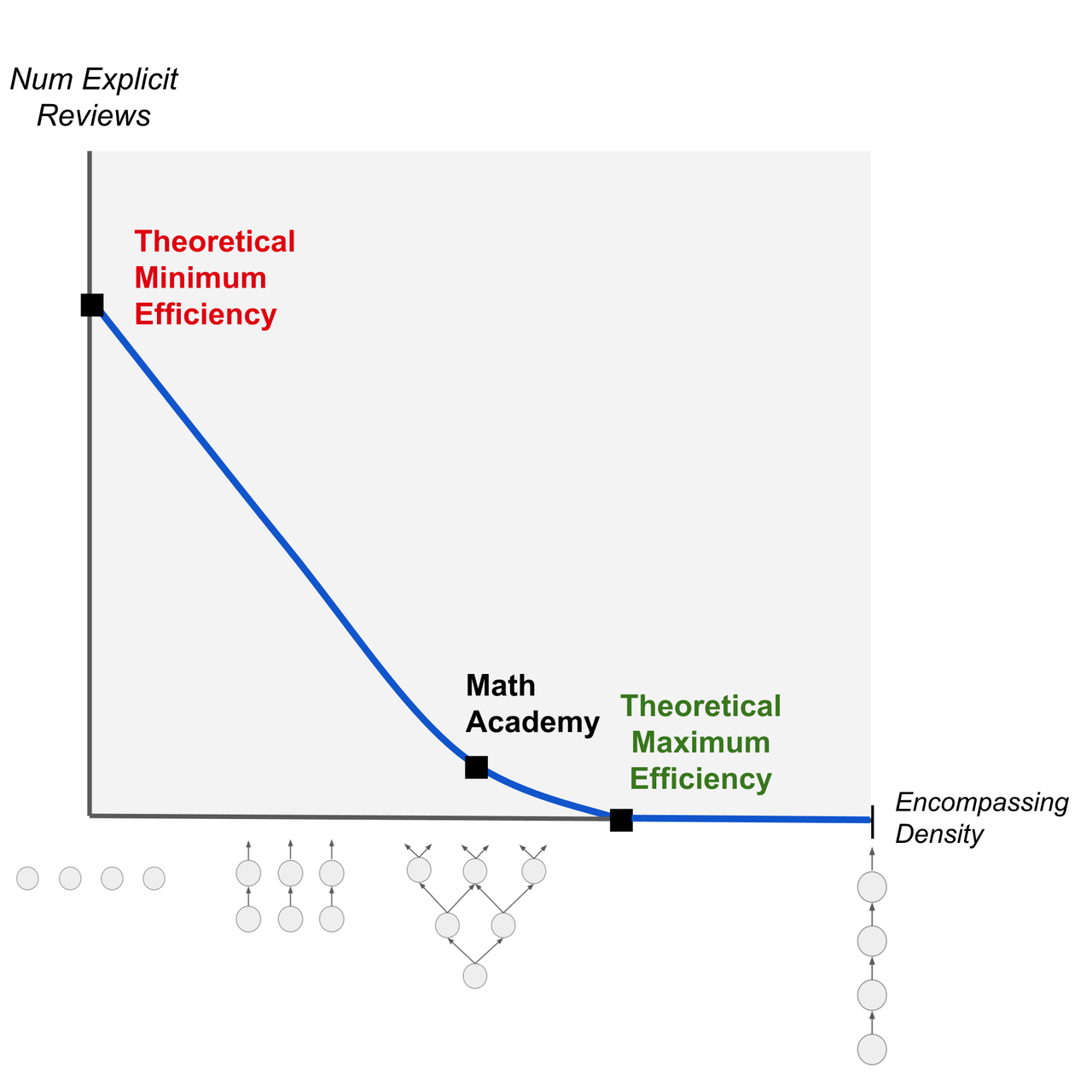
值得强调的是,与 Math Academy 不同,其他间隔重复学习系统并未利用包含关系的强大力量,因此它们只能实现理论最小学习效率。
影响学习效率的因素
请记住,为了实现最大化的学习效率,Math Academy 采用了我们称为重复压缩的流程。我们会收集所有到期需要复习的主题,然后将这些内容压缩成一个小得多的任务集,这个任务集能够:
- 覆盖所有到期的复习内容,以及
- 为你的整个知识体系带来最大的间隔重复学习收益。
你可以将 Math Academy 视为一个装有涡轮增压器的教育引擎,而重复压缩就是我们的燃烧机制。
但请记住,一台引擎如果没有汽油和机油的供应,实际上是无法驱动汽车的。汽油用于产生驱动汽车的能量,而机油则用于防止摩擦导致引擎卡死。
同样的道理适用于 Math Academy。要体验到涡轮增压的效果,你需要:
- 投入足够数量的工作,这些工作可以转化为学习进度,以及
- 确保工作质量足够高,以避免学习过程中出现过度摩擦。
| 表现
通过分析你在各类学习任务中的表现(通过率和准确性),我们能够计算出一个学习效率百分比,用于估计你与课程可能达到的最大效率之间的接近程度。
如果你保持高学习效率,那么只需完成相对较少的工作量,就能在课程中取得显著进步。但如果你的学习效率低下,那么你将需要完成更多工作量才能取得同样的进展。
| 学习效率 | 完成课程所需的工作量 |
|---|---|
| 1 | 1 倍 |
| 0.8 | 1.25 倍 |
| 0.67 | 1.5 倍 |
| 0.5 | 2 倍 |
| 0.25 | 4 倍 |
| 速度
在 Math Academy 中,学习工作量以经验点数(XP)计量。一个 XP 代表一名普通认真(但非完美)学生在完全专注、高效学习状态下一分钟所能完成的工作量。你每个工作日平均完成的 XP 数量,即为你的学习速度。
> 学习效率与速度的关系
尽管学习质量是影响学习效率的首要因素,但学习速度同样会对学习效率产生影响。当你更快地拓展知识边界时,你的知识边界就会更加超前于需要复习的内容,这样我们就更有可能找到合适的主题,帮你一次性「清除」大量待复习的内容。
我们通过实证研究确定了如下关系:
这意味着如果你将学习速度提高一倍,你的学习效率将提升约 2^0.1 = 7%。相应地,如果你的学习速度降低一半,学习效率则会下降约 7%。
> 学习速度与完成时间的关系
在学校正常的课堂时间内,学生通常能够保持至少 40 分钟的完全专注且高效的学习状态。这相当于每个工作日 40 XP 的基准学习进度。
在评估我们课程的 XP 总量时,我们模拟了一名认真但非完美的普通学生,以每个工作日 40 XP 的速度学习。平均而言,假设学生已掌握所有必要的预备知识,一门课程大约包含 3000 XP(这个数字会因所需涵盖的材料量而有较大差异,例如代数预备课程约为 2000 XP,而微积分预备课程则约为 4000 XP)。
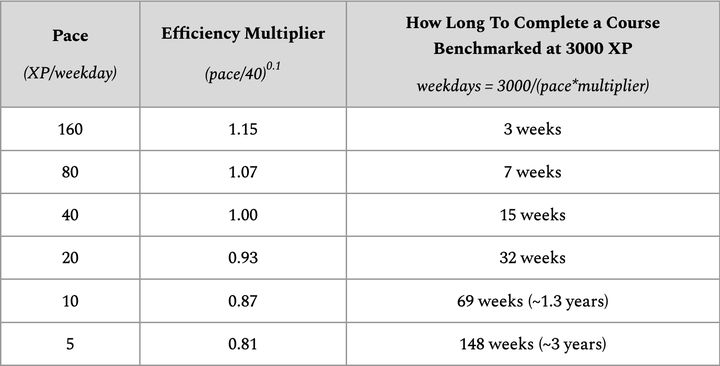
下表展示了按照不同学习速度,完成一门 3000 XP 课程所需的时间。请注意,学习效率是相对于每工作日 40 XP 的基准速度计算的(因此,每工作日 40 XP 的学习速度对应效率系数为 1,更高的学习速度则对应大于 1 的效率系数)。
| 速度 (XP/工作日) | 效率系数 (速度/40)^0.1 | 完成一门3000XP基准课程所需时间 工作日 = 3000/(速度*系数) |
|---|---|---|
| 160 | 1.15 | 3 周 |
| 80 | 1.07 | 7 周 |
| 40 | 1.00 | 15 周 |
| 20 | 0.93 | 32 周 |
| 10 | 0.87 | 69 周 (~1.3 年) |
| 5 | 0.81 | 148 周 (~3 年) |
为了提供一个参照:在传统课堂教学模式中,每个工作日包含 50 分钟的课堂学习时间,以及放学后相同时长的家庭作业。按照这样的学习安排,学生需要一整个学年(36 周)才能完成一门课程。
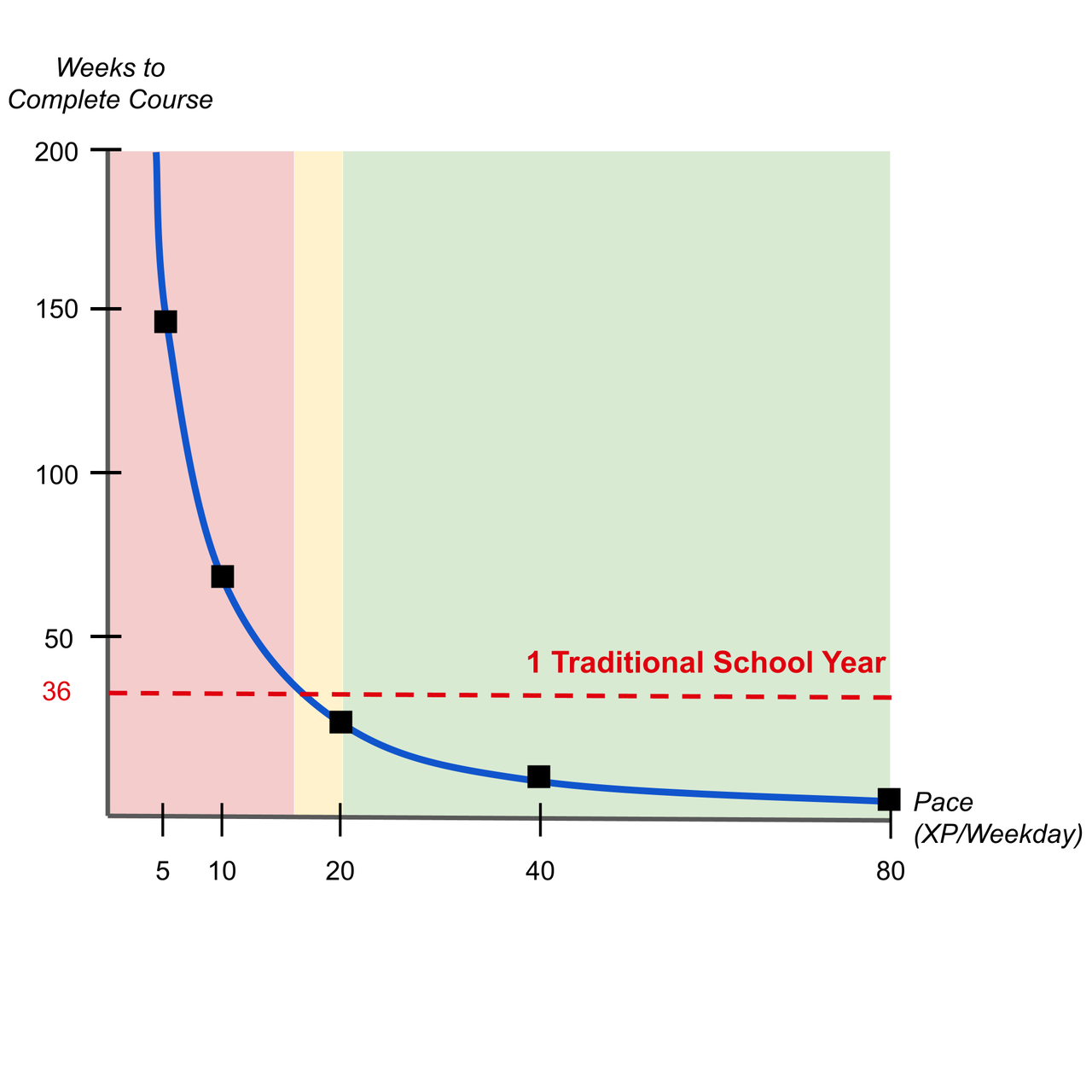
但如果你在 Math Academy 上投入同样的时间(每个工作日 100 XP),你只需 5-6 周就能完成学习!这相当于速度提升了 6 倍以上——而且这并非只有天才才能做到。请记住,我们讨论的是一个认真但并非完美的普通学生。
即使是像 AP 微积分 BC 这样的大型课程(基准约为 6000 XP,是普通课程规模的两倍),学习速度仍然能提高 3 倍以上。如果再考虑到在传统课堂中,你需要额外花时间备考小测验、期中考试、期末考试以及 AP 考试本身,而这些在 Math Academy 的 6000 XP 基准中已经包含了,那么实际上是节省了4倍的时间。
从另一个角度看,如果你像玩手机游戏那样使用 Math Academy,每天只花几分钟,那么你可能需要近十年才能学完传统学校一年的数学课程。
因此,如果你想体验 Math Academy 带来的好处,我们强烈建议你至少保持每个工作日 15 XP 的学习速度。当然,你的学习进度越快,效果就越好。
上一章:
第二十七章 诊断性考试的技术深度剖析 - 知乎下一章:
第二十九章 核心主题优先策略的技术深度剖析 - 知乎Thoughts Memo 汉化组译制
感谢主要译者 claude-3.7-sonnet,校对 Jarrett Ye、白侑
原文:The Math Academy Way: Using the Power of Science to Supercharge Student Learning
参考
1. 第十八章 间隔重复(分散练习) ./1895420939283440005.html2. 第二十二章 游戏化 ./1896510468136341564.html