第三十章 诊断性考试的技术深度剖析

注：本章将展开阐述第四章^[1]和第二十一章^[2]中引入的概念。

⠀⠀⠀摘要：Math Academy 采用自适应诊断技术来推断每位新生的知识画像。这种创新的诊断评估算法是利用知识图谱中的因果关系和基于相关性的推理，来高效且精确地评估学生的知识边界，同时最大限度地减少诊断中的问题数量。该算法能够衡量知识掌握的置信度并处理矛盾信息，使其诊断能够适应诸如前置知识与后继知识的掌握情况，以及准确性与答题时间冲突等微妙场景。对于那些经推断知识掌握置信度较低的领域，系统采用条件性完成机制，从而能够在收集更多关于学生表现的数据时，持续优化其学习定位。

最小化问题数量

如果没有智能算法的支持，我们将需要海量的诊断问题来推断学生的知识边界。课程通常包含多达数百个主题，再加上两倍数量的基础主题——这意味着如果我们从最基础开始，为每个主题都设置诊断问题，那么直到学生无法正确回答为止，我们最终会向学生提出多达 500 多个问题。

然而，Math Academy 通过一种创新的诊断问题选择算法，成功地将诊断问题数量减少了一个数量级。我们的诊断系统对于低年级课程（如前代数）通常只需要 20-40 个问题，对于高年级课程（如微积分）则需要 40-60 个问题。

我们能够实现这种高效诊断的原因有两个：

1. 除了利用知识间的「因果」包含关系，我们还采用了更灵活的基于相关性的推理方法。
   
   
2. 我们预先将知识图谱压缩成最少数量的主题节点，这些节点能以所需精细度完整「覆盖」一门课程及其基础知识体系。

基于这些策略，我们的诊断评估算法在准确性和精确性方面得到了高度的优化。虽然一个完美准确且精确的诊断可能需要多达上千道题目，但是通过牺牲微不足道的准确度和精确度，我们成功将所需题目数量减少了一个数量级。

（当然，高度优化的算法也面临着被错误输入干扰的更大风险——但我们通过检测并重新评估那些可能被错误判断的问题来有效降低这种风险。）

知识置信度和条件性完成机制

| 理论

在诊断过程中，Math Academy 还测量知识置信度，即我们判断学生是否掌握某个主题的信心程度。大多数诊断能够完成并对学生的整体知识状况给出高置信度的评估，但有时也会出现一些置信度较低的区域。这些并非源于诊断覆盖范围不足，而是因为学生的答题表现中出现了矛盾冲突的情况。

主要有两种冲突类型：

1. 前置知识与后续知识的冲突：学生能正确回答较高级主题的问题，却错误回答了较基础的问题，这可能表明学生的知识画像中存在缺口。
   
   
2. 准确性与时间的冲突：学生提交了正确答案，但解题时间过长，这表明他们可能并未真正掌握相应主题。

为了处理这些冲突，我们精心权衡两个矛盾的情形，形成对学生知识状态的高度细致化诊断，就像一位优秀的家教那样，能够根据后续观察恰当地调整评估结果。

特别地，如果评估结果刚好「勉强」达到让学生可以跳过某些主题的临界点，系统会将这些主题标记为有条件完成：系统最初会假定学生已掌握这些主题并据此安排学习任务，但一旦学生在学习过程中遇到困难，系统将立即沿着适当的学习路径进行「回溯」调整。

| 示例

举例来说，假设：

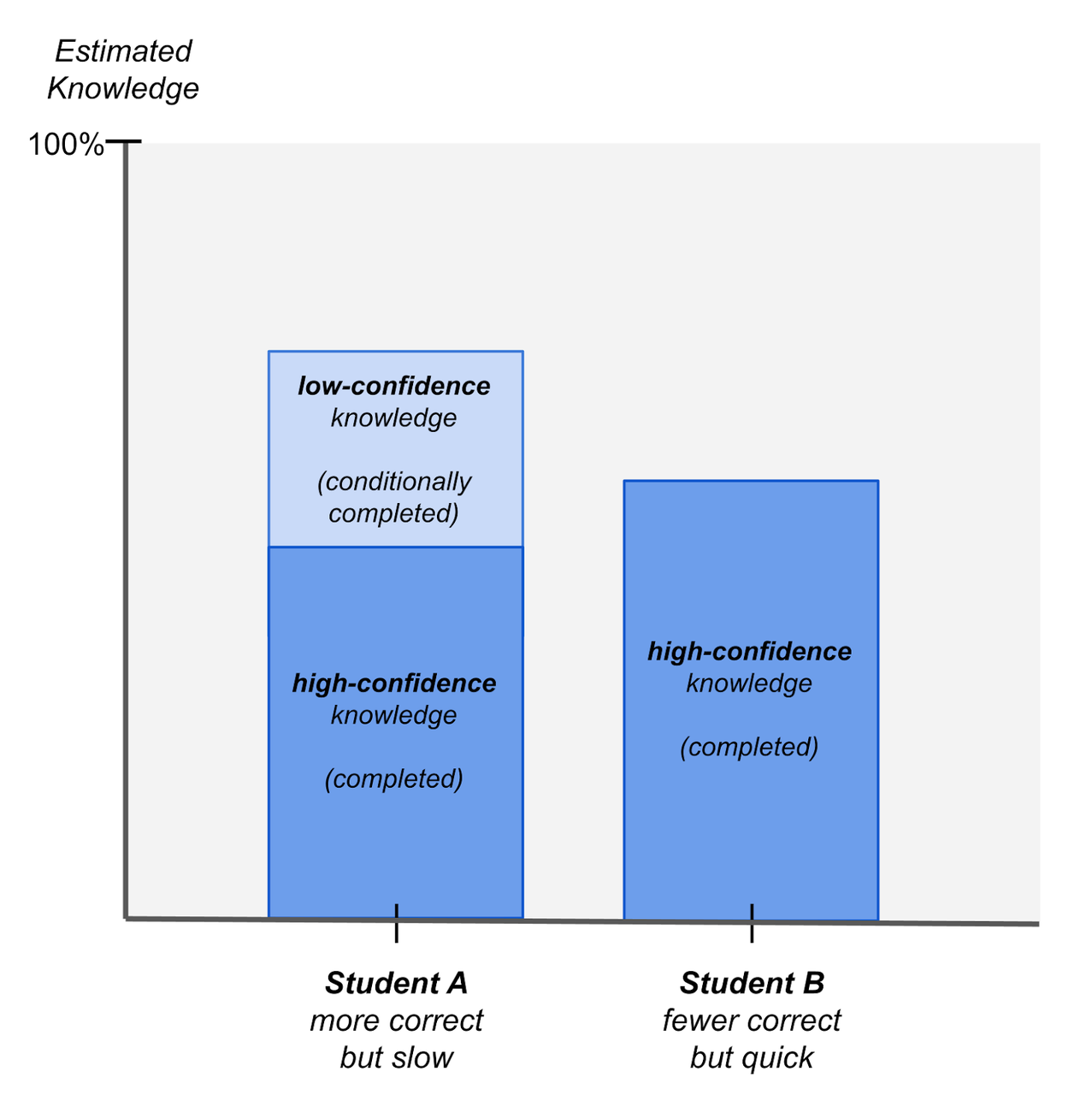
• 学生 A 在诊断测试中答对了很多题，但大多数题目都花费了过长时间；而
  
  
• 学生 B 正确回答的题目较少，但答题又快又自信。

那么结果是：

• 学生 A 会被认为掌握了更多的整体知识，但其中相当一部分是低置信度的知识（如果他们遇到困难，这部分知识可能会被遗忘）；而
  
  
• 学生 B 虽然整体知识量较少，但可能拥有更多高置信度的知识。

| 实现

为了实现这种机制，我们在每个主题上采用正负平衡值来权衡诊断证据。

• 正负号（正数或非正数）用来预测学生是否掌握该主题。
• 平衡值的大小则代表对这一预测的置信程度。

每个答案都关联一个权重，代表其对相应主题正负平衡的贡献。默认情况下，答案权重为 1。然而，如果学生提交了正确答案但花费的时间远超过已掌握该主题的学生的预期时间，那么这个答案的权重会相应降低。虽然这个答案仍然会给学生提供正面评价，但由于解题时间越长（超过合理时间标准），那么获得的正面评价就越少。
一旦确定了答案的权重值，它会在整个知识图谱中传播，相应地更新各主题的正负值平衡：

• 一个正确的答案会提高该回答所涉及主题及其前置知识点（以及这些前置知识点的前置知识点，以此类推）的正负值平衡，而
  
  
• 一个错误的答案则会降低该回答所涉及主题及其后续知识点（以及这些后续知识点的后续知识点，以此类推）的正负值平衡。

在处理完所有诊断性问题后，任何具有正向正负值权重的主题都会等同于其正负值平衡数量，被记入重复练习次数。

保守型与激进型掌握边界

曾经有这样的情况：学生完成了某门课程，随后参加了同一课程的分级测试，却惊讶地发现测试结果显示他们在该课程中的知识水平比预期低。但这实际上是一个正常的结果，尤其对于基础较弱的学生而言。

学生成功完成了课程的所有作业，并不意味着他们能在该课程的综合期末考试中取得优异成绩。这一点在分级测试中尤为明显，因为分级测试比普通考试更具挑战性：与普通考试不同，

• 分级测试必须覆盖每一个知识点（包括所有最难的主题），并且
  
  
• 它必须包含每个知识点中最高级别的问题类型（如果学生只会解决简单情况，我们就不能让他们跳过该知识点）。

此外，虽然我们常常将学生的「掌握边界」描述为贯穿学生知识图谱的单一界线，但实际上学生拥有的是一个「掌握区域」，其下限是保守型掌握边界，上限则是激进型掌握边界。分级测试测量的是保守型掌握边界，而基于掌握的分层学习则是在激进型掌握边界上运作的。

当学生成功完成一节课程后，他们已经充分掌握了该主题的知识，足以继续在已学内容的基础上叠加学习新知识，但他们可能还未达到对该主题的自主运用程度。打个比方，就像体操运动员在训练中学习新动作时，需要一段时间的练习，才能在比赛中自信展示这项技能，但这并不妨碍他们在此期间继续训练更高难度的动作。

补充诊断

随着知识图谱中不断添加新主题和修订知识连接关系，从学生初始评估诊断中推断出的知识画像可能会逐渐过时。当这种情况发生时，我们会安排名为补充诊断的小型测评，以更新学生的知识状况。

补充诊断所涵盖的主题是那些在原始诊断中未直接评估过的，并且在考虑原始诊断及之后所有评估答案时，正负权重平衡为零的主题。补充诊断采用与原始诊断相同的高效推断方法，因此通常规模较小，最多只包含几个问题。

选择优质的诊断问题

为特定主题选择一个好的诊断问题需要考虑许多细微因素。

• 一方面，诊断性问题不能过于简单。每个诊断性问题应当具有足够的难度，使得当学生能够正确作答时，专业导师或教师能够判断出该学生已经完全掌握了相应的知识点。
  
  
• 此外，诊断性问题应当考察相应主题的所有前置知识。否则，如果某个前置知识未被问题覆盖，那么即使学生不了解这一前置知识，也可能正确回答问题，从而错误地被认为掌握了这些前置知识。
  
  
• 尽管如此，诊断性问题通常不应是其对应主题中最具挑战性的问题。问题越复杂，学生就越有可能因为一些小失误而犯错。

因此，每个诊断性问题应当选择为最简单的问题，同时满足：

1. 能够让专业导师或教师确信学生已经掌握了相应的主题，并且
2. 考察了该主题的所有前置知识。

在实际操作中，由于需要考虑诸多细微因素，我们通常通过人工方式选择诊断性问题。

上一章：

下一章：

Thoughts Memo 汉化组译制
感谢主要译者 claude-3.7-sonnet，校对 Jarrett Ye、白侑
原文：The Math Academy Way: Using the Power of Science to Supercharge Student Learning

← 返回目录