为什么美国中小学生学的数学比我们简单，美国人却还能做出超级牛的东西？

知乎惯例，先问是不是，再问为什么。美国初高中生学数学究竟学什么？真的比中国学生学得简单吗？想搞明白这个问题，首先得了解一下共同核心标准（Common Core），定义了美国学生从幼儿园到高中（K-12）在语文和数学上的学习标准。这东西有点类似国内的新课标，但没有规定要用什么教材、要怎么教，只划定了要学什么。

我对美国数学教育的了解并不多，仅限于 Math Academy 的课程安排。他们的安排是这样的：六年级学生从预代数开始，在八年级前完成全部高中数学内容（代数 I、几何、代数 II、预微积分），然后在八年级学习 AP 微积分 BC 并参加 AP 考试，高中阶段则学习完整的本科数学课程^[1]。

这是他们四到八年级（美国是初中两年高中四年，从九年级开始上高中）的课程路线图：

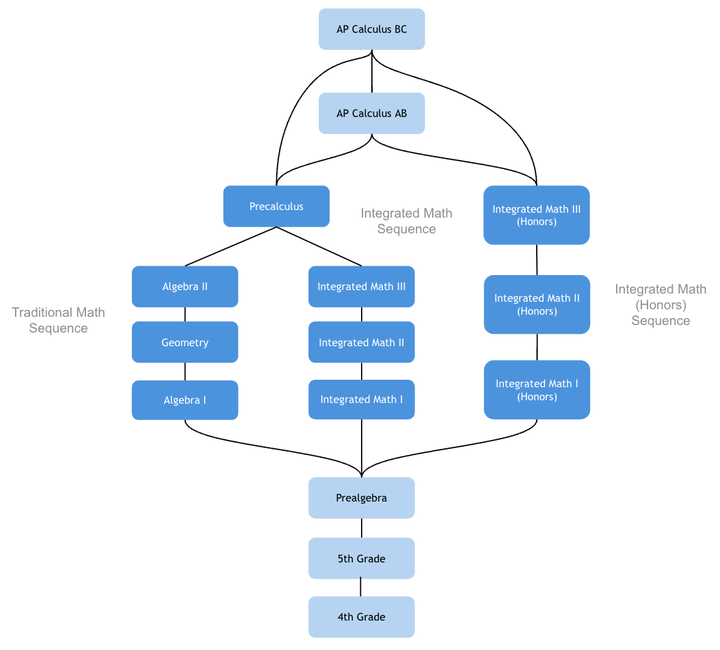
他们得到了 Accrediting Commission for Schools 和 Western Association of Schools and Colleges 的认证，所以这个课程是符合共同核心标准的，我简单翻译一下这些课程的要求。

AP 微积分 BC

来源：AP Calculus BC

成功完成本课程后，学生将具备以下能力：

• 掌握极限的概念，包括根据图像估计极限、极限的运算法则、函数极限、运用代数技巧求解极限，以及涉及三角函数的特殊极限。
• 理解连续性，包括函数在某一点连续的定义、间断点的分类、可去间断点的处理，以及介值定理。
• 学习微分基础，包括瞬时变化率、利用定义计算导数、求导法则、指数函数、对数函数、三角函数和反三角函数的求导、求解切线与法线方程、链式法则、隐函数求导，以及反函数的求导。
• 探究微分的实际应用，包括在具体情境中解释导数的含义、估算导数值、相关变化率问题，以及洛必达法则。
• 理解如何运用微分来近似函数值并解决最优化问题。
• 进行曲线分析，包括中值定理、极值定理、运用一阶与二阶导数判别法分析临界点、函数的凹凸区间、拐点，以及根据导数信息绘制函数图像。
• 深入理解积分，包括不定积分、运用黎曼和近似计算面积、定积分，以及运用微积分第一基本定理计算曲线下面积及其他应用。
• 将积分理解为累加函数，并掌握其与微积分第二基本定理的关系、涉及累加函数的最优化问题，以及对密度函数的理解与应用。
• 熟练掌握高级积分技巧，如换元积分法、分部积分法、三角换元法、部分分式分解法，以及反常积分。
• 掌握微分方程基础，包括可分离一阶常微分方程的建模与求解、常微分方程的定性分析、指数增长与衰退模型、逻辑斯蒂增长模型、斜率场，以及运用欧拉方法求解数值解。
• 探索积分的应用，如求解函数平均值、曲线围成的面积、平面光滑曲线的弧长、已知横截面的立体的体积，以及旋转体的体积。
• 掌握参数方程的微分与积分，求解参数曲线的切线与法线方程、计算弧长，并理解参数方程与向量值函数之间的联系。
• 理解极坐标下的微积分，涵盖求导、切线与法线、求解极坐标区域的面积，以及计算极坐标曲线的弧长。
• 研究质点运动学，包括直线运动和平面运动中的位移、速度和加速度，并运用积分联系三者关系。
• 牢固掌握数列与级数，包括数列的极限、单调数列、无穷级数的收敛与发散、几何级数，以及各类敛散性判别法。
• 探究幂级数与泰勒多项式，包括收敛半径与收敛区间、麦克劳林级数与泰勒级数、利用已知幂级数展开函数、幂级数的求导，以及运用泰勒级数近似计算积分。
• 熟练运用图形计算器进行表达式求值、求解方程的根、交点、极值、导数、定积分、反常积分，以及探究函数与曲线的性质。
• 将微积分概念应用于解决物理、工程、经济等领域的实际问题。

预微积分

来源：Precalculus

成功完成本课程后，学生将具备以下能力：

• 探究有限等差数列与等比数列，并运用其为金融等现实世界问题建立数学模型。
• 应用二项式定理，并阐明其与帕斯卡三角（杨辉三角）的内在联系。
• 掌握有理表达式的化简与运算，并能求解有理方程。
• 系统性分析有理函数的性质，包括其端点行为、根、垂直渐近线和可去间断点；能运用极限的概念描述函数的行为，并理解有理函数的封闭性。
• 求解各类不等式，包括二次不等式、高次多项式不等式、含绝对值的不等式、二元不等式及分式不等式。
• 将圆锥曲线的知识体系扩展至椭圆和双曲线，包括推导其标准方程，并熟练运用焦点、准线、离心率等核心性质。
• 掌握各类三角恒等式，包括勾股恒等式、余函数恒等式、和差角公式及倍角公式。
• 求解各类三角方程，包括掌握其通解、处理涉及函数变换的复杂情形，以及求解二次形式的三角方程。
• 为参数方程的学习奠定坚实基础，包括绘制参数曲线、求解交点，以及掌握常见圆锥曲线的参数方程表示法。
• 深入理解极坐标系与极坐标方程，掌握直角坐标与极坐标的互化方法，并能绘制与分析常见极坐标曲线。
• 全面掌握复数理论，包括理解复数运算的几何意义、复数的三角形式与指数形式、棣莫弗定理、欧拉公式、复数方根、代数基本定理以及多项式恒等式的推广应用。
• 熟练进行向量运算，包括向量加法、标量乘法、点积及叉积。
• 掌握矩阵的基础知识，包括矩阵的加、减、乘、数乘运算以及行列式的计算，并能应用矩阵解决线性方程组问题、执行平面内的线性变换。
• 扎实掌握概率论与组合数学，包括排列与组合、复合事件、条件概率、离散型随机变量（含二项分布和几何分布）以及正态分布。
• 初步涉猎大学水平的统计学，包括学习方差、协方差、线性相关以及线性和非线性回归等核心概念。

代数 II

来源：Algebra II

成功完成本课程后，学生将具备以下能力：

• 理解实数体系的层级与性质，包括对自然数、整数、有理数及无理数的分类。
• 掌握循环小数与分数的互化方法，并阐述有理数与无理数运算的封闭性等一般性质。
• 掌握复数的基本概念及其四则运算。
• 求解含虚数解与复数解的一元二次方程，并理解虚数单位i的周期性。
• 求解单项式与多项式的最大公因式及最小公倍式。
• 运用多种技巧对多项式进行因式分解，包括提公因式法、平方差、立方和/差公式、分组分解法以及对特定高次多项式的因式分解。
• 掌握多项式的长除法、综合除法，以及有理表达式的运算。
• 应用因式定理、余数定理及有理根定理求解多项式方程。
• 绘制多项式函数图像，并分析其端点行为、根等关键特征。
• 辨别一一映射函数与可逆函数，掌握通过限制定义域或值域构造可逆函数的方法，并理解原函数与其反函数的定义域和值域关系。
• 分析函数的局部极值、周期性、奇偶性及无界性。
• 计算函数在指定区间上的平均变化率。
• 掌握函数图像变换，包括平移、伸缩、反射及其组合变换，并能处理含绝对值的图像变换。
• 确定变换后函数的定义域和值域，并能在变换后的图像上定位关键点。
• 掌握指数式与对数式的互化，能计算对数值，并运用对数运算法则化简表达式。
• 求解各类指数方程与对数方程，包括处理不同底数的情形。
• 绘制指数函数与对数函数的图像，并理解其图像的关键性质。
• 运用指数函数为现实世界情景建模，包括处理复利与连续复利等金融问题。
• 掌握有理表达式（分式）的四则运算与化简。
• 绘制并分析倒数函数与一般有理函数，包括确定其渐近线、根、截距和端点行为。
• 掌握倒数函数的组合变换，并分析其定义域、值域和反函数。
• 掌握根式的化简与运算，求解根式方程，并能检验并舍弃增根。
• 绘制并分析根式函数，包括确定其定义域、值域、截距等图像关键特征。
• 掌握圆的标准方程与一般方程，并能运用配方法由方程求出圆心和半径。
• 求解圆、抛物线与直线的交点问题，并计算其截距。
• 理解并应用抛物线的焦点-准线定义。
• 掌握三角学基础，包括三角函数的定义、弧度制以及单位圆的应用。
• 掌握三角函数的图像绘制与性质分析，包括应用图像变换并描述变换后的性质，并能运用三角函数模型解决现实世界问题。
• 推导并应用正弦定理与余弦定理，解决现实情境中的解三角形问题。

几何

来源：Geometry

成功完成本课程后，学生将具备以下能力：

全等、相似与证明

• 证明对顶角定理。
• 证明有关平行线的内错角、同旁内角、外角等定理及其逆定理。
• 证明邻补角垂直定理、垂直平分线定理及其逆定理。
• 将平移、轴对称、位似、拉伸及复合变换应用于二维图形。
• 运用函数表示坐标平面中的几何变换，并用其求出图形的像。
• 理解并应用 ASA（角边角）、AAS（角角边）、SAS（边角边）、SSS（边边边）和 HL（斜边直角边）三角形全等判定准则。
• 阐释如何运用刚体运动（等距变换）证明两个图形全等。
• 理解并应用全等关系所具有的自反性、对称性和传递性。
• 证明两个三角形全等，并应用「全等三角形的对应部分相等」（CPCTC）的性质。
• 理解多边形的相似性，包括处理面积比的计算，并阐释如何运用相似变换证明两个多边形相似。
• 理解并应用 AA（角角）、SSS（边边边）和 SAS（边角边）三角形相似判定准则。
• 证明两个三角形相似，并应用「相似三角形的对应部分成比例」（CPSTP）及「相似三角形的对应角相等」的性质。
• 理解并应用三角形中位线定理和三角形比例定理。
• 证明三角形中位线定理。

圆与弧度制

• 圆的基础知识：半径、直径、弦、圆内与圆外、周长、弧、扇形和弓形。
• 计算圆与扇形的周长和面积，并解决相关问题。
• 解决有关圆周角的问题，包括应用圆周角定理、泰勒斯定理，以及圆内接四边形的相关问题。
• 解决有关圆的切线问题（含两切线、两割线、一割线与一切线等情况），并应用弦切角定理。
• 证明所有圆都相似。
• 理解弧度，进行弧度与角度的换算，并运用弧度计算弧长和扇形面积。

坐标几何

• 处理坐标平面中的平行线与垂直线。
• 距离公式及其推导，并运用该公式求解点到直线的距离。
• 分割有向线段，解决相关问题，并应用中点公式。
• 计算坐标平面内多边形的周长与面积。
• 求解坐标平面内圆的方程。
• 通过配方法确定圆的圆心与半径。
• 计算圆的截距，并求解圆与直线的交点。
• 求解圆的切线方程。
• 运用直径和弦的垂直平分线性质解决坐标平面中的问题。
• 在坐标平面中应用泰勒斯定理。

三角形、四边形与三角学

• 理解、应用并证明三角形外角定理。
• 理解并应用勾股定理及其逆定理。
• 掌握 45-45-90 度和 30-60-90 度特殊直角三角形。
• 计算 45-45-90 度、30-60-90 度特殊直角三角形和等边三角形的面积。
• 证明三角形内角和等于 180 度。
• 证明等腰三角形定理及其逆定理，以及其他相关结论。
• 理解三角形的中线和重心，应用重心比定理，并求解三角形的重心坐标。
• 证明重心定理和重心比定理，并推导三角形的重心坐标公式。
• 证明平行四边形的性质，以及有关平行四边形和矩形关系的定理。
• 运用三角比计算直角三角形的边长和角度。
• 掌握倒数三角比。
• 识记特殊角的三角比及其推导过程。
• 理解相似直角三角形中三角比的关系。
• 运用三角学知识计算直角三角形的面积。
• 理解直角三角形中的余角，以及三角函数与其互余函数的关系。
• 运用三角学为现实世界及数学问题建模求解，包括涉及多个直角三角形的案例。

立体几何

• 识别三维图形，并正确应用与立体几何相关的术语。
• 利用几何体的展开图计算表面积。
• 应用三维空间中的距离公式。
• 应用多面体的欧拉公式，并理解五种柏拉图立体的意义。
• 处理相似立体的表面积和体积关系。
• 计算各类三维图形的表面积和体积，包括正方体、长方体、棱锥、圆柱、圆锥、球体及正棱台。
• 计算旋转体的体积。

概率与组合学

• 掌握概率论基本概念，包括样本空间、对立事件、复合事件和维恩图。
• 计算涉及事件并集与交集的概率，并运用这些思想解决现实世界的问题。
• 应用加法法则并理解互斥事件。
• 掌握条件概率，包括乘法法则及其推导、全概率公式、独立事件和树状图。
• 应用加法原理和乘法原理。
• 确定元素的排列方式，并计算排列与组合。
• 运用组合学方法计算概率。

代数 I

来源：Algebra I

成功完成本课程后，学生将具备以下能力：

• 掌握线性方程（一元一次方程），包括含有一个或多个待定系数的方程，并能将其应用于解决涉及连续整数、行程、工程及混合物等类型的实际问题。
• 熟练求解线性不等式。学生将学习使用区间表示法描述解集，求区间的并集与交集，解不等式组，绘制不等式解集的图像，并运用不等式对实际情景进行建模。
• 熟练掌握二元一次方程，包括其点斜式和标准式，并能熟练判定直线的性质。学生还将能够描述坐标平面中平行线与垂直线的位置关系。
• 精通运用代入消元法和加减消元法求解二元一次方程组，包括处理系数为分数和小数，以及无解和有无穷多解的情况。学生将能把方程组的解与两直线交点联系起来，并运用所学进行情景建模。此外，学生将初步接触非线性方程组。
• 求解简单的平方根、立方根和高次根方程，并能识别无实数解的情况。
• 加深对单位及其应用的理解，包括运用代数方法进行单位换算，以及处理正、反比例关系问题。
• 探究根式和分式，并培养处理和求解相关方程的能力。
• 开启函数的学习之旅。学生将接触到函数的多种表示法、垂直线检验法、定义域、值域、全局最值、末端趋势、函数的单调性、函数的运算（包括函数复合）以及反函数等核心概念。
• 掌握绝对值的运算法则，求解简单的绝对值方程和不等式，并能绘制和分析绝对值函数的图像。
• 为指数方程和指数函数的学习打下坚实基础，包括代数式的化简、方程的求解、指数函数图像的绘制，及其在指数增长和衰减模型中的应用。
• 熟练掌握多项式的运算，包括多项式的化简、加、减、乘和因式分解。
• 运用多种方法求解二次方程，包括应用零乘积法则、配方法和求根公式。
• 绘制并分析二次函数的图像，运用多种方法计算对称轴，并求解直线与二次函数的交点。
• 运用二次函数对竖直运动、营收、成本及利润等真实世界情景进行建模。
• 理解数列的规范表示法，掌握递推数列、等差数列、等比数列及其应用。

预代数

来源：Prealgebra

成功完成本课程后，学生将具备以下能力：

• 解决有关比例、百分比、单位速率和比例关系的问题，并能运用这些概念解决实际问题。
• 掌握负数和有理数的加、减、乘、除四则运算，并解决相关的实际问题和数学问题。
• 理解并应用数论的基本概念，如整除性法则、算术基本定理，并将素数、素因数分解与已学过的最大公因数、最小公倍数等概念建立联系。
• 熟练运算含指数和根式的代数式，包括分数指数、负指数、指数与根式的运算法则，以及科学记数法。
• 遵循运算顺序对包含负数、有理数、分数指数、负指数及根式的复杂表达式进行求值。
• 构建、求值、化简和因式分解代主式，包括对简单分式的基本处理。
• 求解单步和多步的线性方程与不等式，包括涉及分式、交叉相乘法和多个变量的情况。
• 绘制线性方程的图像，计算并描述图像的关键特征，并掌握斜截式。
• 使用代入法求解方程组，并解释其解与两直线交点的几何意义。
• 理解并应用基本几何概念，包括线段、角及其性质，三角形及其分类，多边形与四边形，以及各类图形的面积与周长计算。
• 通过集中趋势、离散程度、偏态和离群值等概念来概括和呈现数据，并使用频数分布表、点图、箱线图和直方图实现数据可视化并解读其分布。

五年级数学

来源：5th Grade Math

成功完成本课程后，学生将具备以下能力：

• 构建并计算数值表达式，包括含有多重括号的算式。
• 理解负数，能在数轴上表示和比较负数，并理解绝对值的概念。
• 掌握单位数及多位数的乘法。
• 熟练进行整数除法，包括理解余数的意义，并能运用多种策略完成除数是两位数的除法。
• 掌握异分母分数和带分数的加减法，能借助直观模型解释运算，并解决相关应用题。
• 掌握分数乘法的概念，包括带分数的乘法运算。
• 能够计算分数除法，包括除以整数和分数，理解并应用倒数的概念，并解决相关的实际问题。
• 理解并应用小数的数位系统，能以多种形式读写小数、比较大小、进行取舍，并初步了解有效数字。
• 能够估算小数，并进行小数的加减运算，包括处理小数位数不同的情况。
• 运用多种策略进行小数的乘除法，包括掌握标准竖式算法。
• 在进行小数乘除法时，能对积和商进行估算。
• 理解指数的意义，并能计算底数为整数、分数和小数的指数表达式。
• 能在公制单位和英制单位之间进行换算。
• 运用线状图表示和解读数据，包括含有分数的数据。
• 理解并运用坐标解决实际问题，并在地图上表示位置。
• 识别、描述和比较数据中体现的数字规律和关系。
• 使用小正方体和公式计算长方体的体积，并解决涉及体积和二维图形分类的实际问题。
• 能根据图形的属性，按层级关系对四边形进行分类。

四年级数学

来源：4th Grade Math

成功完成本课程后，学生将具备以下能力：

• 掌握整数的数位知识，包括比较多位数的大小和进行取近似数。
• 掌握七位数以内多位整数的加减法。
• 运用面积模型和数位策略进行多位数乘法。
• 运用面积模型、盒子模型和数位策略进行多位数除以一位数的除法。
• 掌握多位数加、减、乘、除的估算方法。
• 掌握分数的基础知识，包括分数的性质与等值分数、通分、化简为最简分数，以及带分数与假分数的互化。能运用多种策略比较分数大小。
• 掌握同分母分数及带分数的加减法，以及分数与整数的乘法。
• 初步认识小数，包括小数与分数的互化、比较小数大小，以及进行小数的加法。
• 测量与数据：认识常用的计量单位并进行换算，能运用线状图表示和解读数据。
• 几何基础：认识点、线、射线、线段、平行线、垂直线、圆和角，并掌握角的度量。
• 代数思维初步：学习用字母表示数，建立并解决简单的数学问题，发现并推导数字之间的规律。
• 在整个课程中，通过解决多步骤的实际问题和数学问题，来综合运用所学技能。

了解完这些，我不觉得还有人会问「为什么美国中小学生学的数学比我们简单？」这种问题了。

另外，如果要研究美国数学教育的话，SMPY 也是一个不可错过的资料。这里简单介绍一下：

「数学早慧青年研究」（Study of Mathematically Precocious Youth，简称 SMPY；官网主页）是一项由 Julian Stanley 创立的、针对高智商学生的纵向「人才搜寻」研究。它尤其关注在初中阶段就在 SAT 数学部分（SAT-M）取得高分的数学天才（目标是筛选出万里挑一的人才）。该研究发源于马里兰州地区，现已扩展至美国大部分地区。SMPY 不仅研究这些早慧青年，还资助他们参与高级课程和接受加速教育，这些项目通常与其大本营——约翰霍普金斯大学合作举办。

← 返回目录