要简单地解释 Anki 中制卡与复习之间的关系,可以将制卡看作编码记忆的过程。编码越精细,后续的复习就会越轻松[1]。当然,长期以来,我们并没有对这一影响做详尽的分析。本期我们将引入之前所提及的记忆模型,将制卡对复习的影响量化,让大家直观地感受到制卡的重要性。
为了让大家更清楚地看到制卡与复习效率的关系,我用 Python 编写了一个简单的复习模拟器,输出一些模拟结果的可视化图像供大家参考。
模拟脚本地址:
https://github.com/L-M-Sherlock/space_repetition_simulators模拟条件
- 间隔系数:2.5
- 保留率:0.9
- 初始间隔:1
- 新卡片总量:10000
- 每日新卡片上限:50
- 每日复习上限:不限
- 模拟周期:300 天
基准情况
我们先以 Anki 算法的默认参数作为基准,假设一个人的制卡水平一般,那么他的复习过程会近似于 Anki 默认的复习规划。
每日的复习量模拟如下:
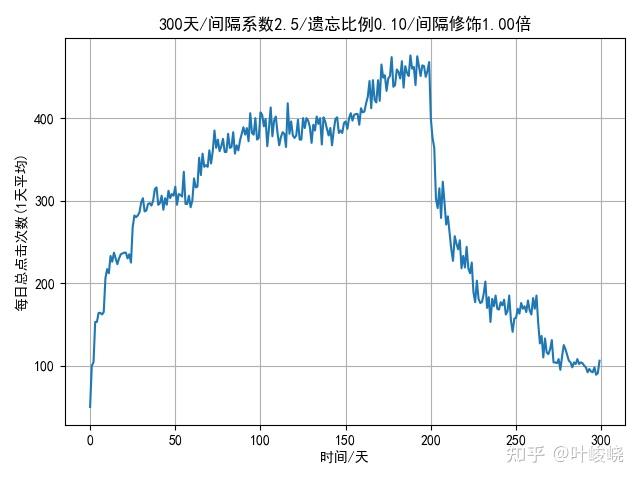
- 总重复次数:88515
- 平均每日重复次数:295
制卡水平
以上图为基准,我们就可以根据制卡水平来调整模拟参数,从而对比不同学习者的复习效率。
什么?怎么判断制卡水平?这个看起来很难量化,但是只要我们从复习行为的角度来看,就能将制卡水平转换为记忆稳定性的初始值[2][3]。
怎么理解呢?这里就需要看看 SuperMemo 的做法了。SuperMemo 会根据学习者的复习反馈,逐步调整间隔,保证每次复习都是发生在回忆概率为 90% 的时刻。那么只要我们看看第一个间隔的长度,就能知道记忆稳定性的初始值。而我们不断复习的目标,实际上就是不断提高记忆稳定性。记忆稳定性的初始值高,就相当于领先在起跑线上。
好了,废话不多说,先看看我自己用 SuperMemo 这几个月来,SuperMemo 算法估计的第一个间隔长度吧:
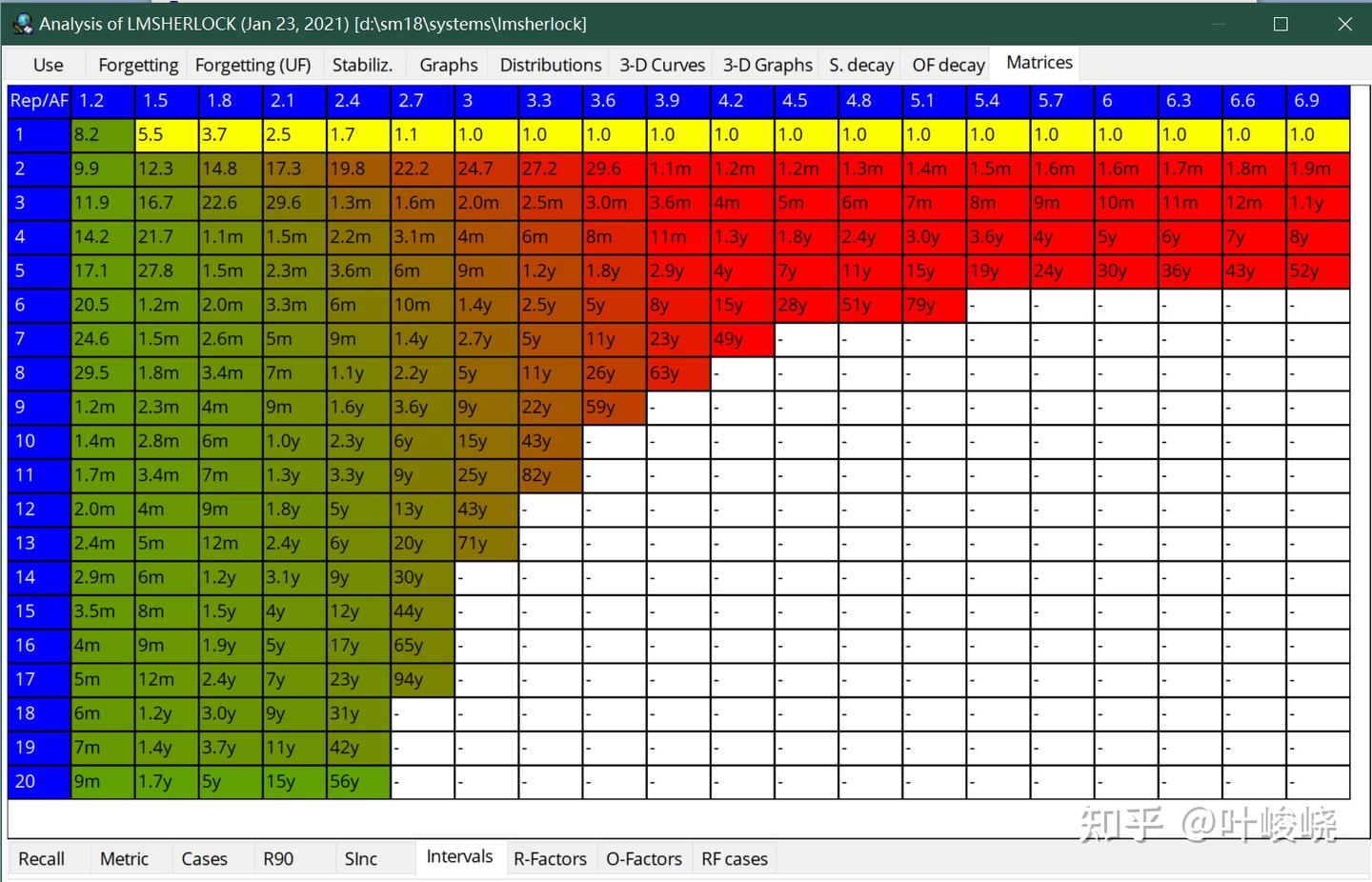
8.2 约等于 8,也就是说我复习的第一个间隔是 8 天。如果在 Anki 中,新卡片的毕业间隔是 1 天,即使是简单间隔也有 3 天[4]。让我们看看如果记忆稳定的初值为 8,模拟的结果如何:
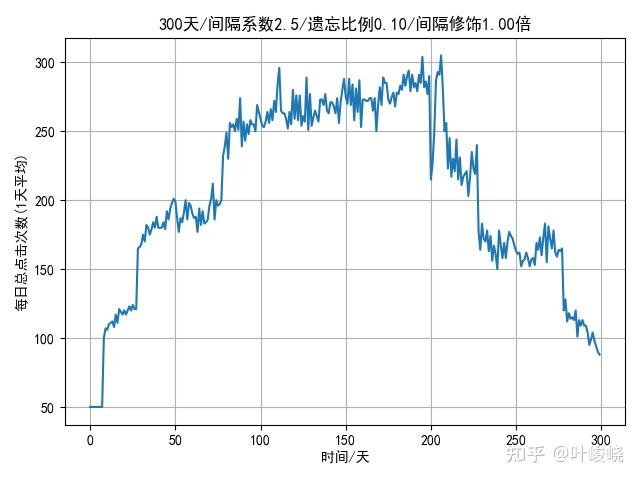
- 总重复次数:62130
- 平均每日重复次数:207
比基准情况整整少了 1/3,而基准情况其实已经比一些批量制卡要好上不少了。
如果卡片做的差一点(大段文字直接糊上去、批量制卡等等),每天的保留率都达不到 90%,那么模拟的结果可能是:
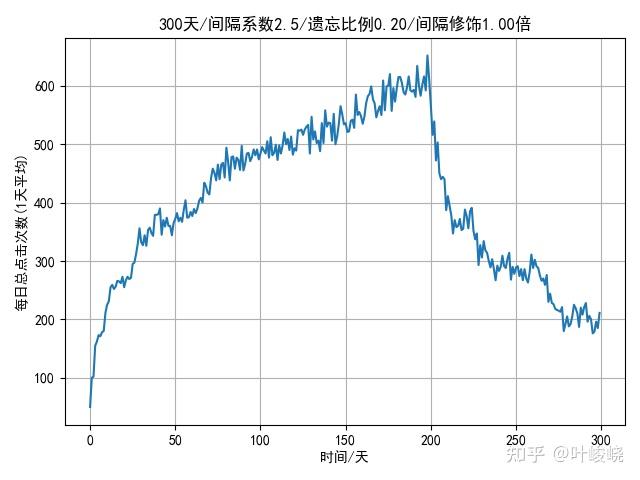
- 总重复次数:120123
- 平均每日重复次数:400
比基准情况多了 1/3,更是比我的模拟结果多了整整一倍。由此可见,不同的制卡习惯所造成复习过程的差异可能会很大。
另外,本模拟没有考虑每次复习的回忆时间。从直觉上来说,下功夫做的卡片回忆起来更快,那么好好制卡的效率就更高了。
进一步阅读
本期重点论述了制卡对复习效率的重要影响,建议大家制卡时多下功夫。关于如何制卡,以前写过/翻译过很多相关文章,我整理了一个收藏夹,方便大家查阅:制卡原则与知识表述本期重点论述了制卡对复习效率的重要影响,建议大家制卡时多下功夫。关于如何制卡,以前写过/翻译过很多相关文章,我整理了一个收藏夹,方便大家查阅:
制卡原则与知识表述参考
1. 记忆研究者反复发现对记忆的编码越精细,记忆也就会更持久。精细的编码本身就相当于你构造的联系的丰富程度。 https://zhuanlan.zhihu.com/p/651317222. 记忆稳定性是指一批记忆在一次复习后遗忘率达到 10% 所需的时间。 ./343115387.html
3. 值得注意的是,随着复习的早期进行,稳定性往往急剧增加,并且在几十年后接近极低的稳定性增长水平。这可以解释为这样一个事实,即记忆在个体的整体知识结构中找到了自己的位置,获得了高度的稳定性 ./268782211.html
4. 毕业间隔:学习新卡片后连续选择【一般】的间隔; 简单间隔:学习新卡片后选择【简单】的间隔; ./42921090.html

