学习的时候，怎么理解知识？怎么更快的理解知识？

问题描述

答案是重构知识，形成自己的知识结构。由于文字天然是线性的，而知识结构是网状的，理解知识的第一步就是理解文本，将承载知识的文本重构成概念网络。

那怎么重构呢？先拆解，再整合。

怎么拆解？不断发问，对文本提问，然后尝试用文本内容来回答。

在这个过程中，你将会把文本中的概念与观点与自己已有的知识联系起来。同时你将会推断作者意有所指但没有成文的细节。

这样一来，你就会逐步整合出自己的概念网络。

这样说有点抽象，这里有几个例子可供参考：

以下内容摘自 @Thoughts Memo 汉化组的译文《间隔重复的有效实践》

示例

以下许多例子可能过于详尽：我们制作的抽认卡数量远超主题实际所需。但这是为了阐释一般规则。随着经验的积累，你会逐渐掌握某个特定主题需要多少问题，而且你的知识网络中不同部分之间的联系程度也会有所不同。

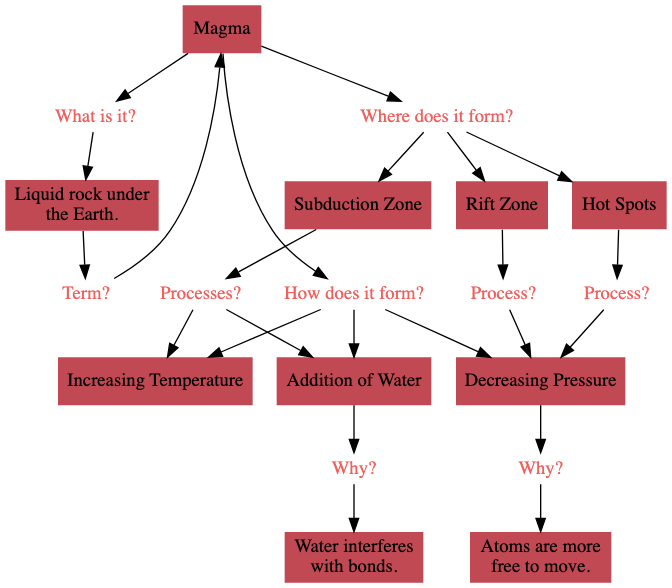
示例：岩浆的形成

以下内容摘自我的地质学笔记：

——————

岩浆是存在于地球表面以下的液态岩石。

形成岩浆的三个过程是：

温度升高：温度升高可以使岩石熔化。
压力降低：当压力降低时，原子能够更自由地移动，岩石就会转变为液态。
加入水分：水能降低岩石的熔点，因为水分子会破坏岩石的晶体键。

岩浆在三个地方形成：

热点： 地球深部的高温岩石在上升过程中，由于周围压力逐渐降低，最终熔化形成岩浆。
裂谷带： 当地壳板块分离时，下方密度较小的热岩石会上升填充裂隙。随着压力减小，这些岩石开始熔化。
俯冲带： 含水量丰富的海洋板块下沉至地幔。水分受热后上升，渗入上方的岩石中，引发岩石熔化。

——————

让我们系统地整理这些信息。我们需要记住三个要点：

岩浆的定义
岩浆的形成过程
岩浆的形成地点

首先是岩浆的定义：

问题	答案
岩浆是什么？	地球表面以下的熔融岩石。
地球表面以下的熔融岩石叫什么？	岩浆。

接下来，我们需要了解岩浆的形成过程。值得注意的是，我们应该将形成过程列表和其详细解释分开，以保持每个学习要点的简洁性。

因此，我们先列出岩浆的形成机制：

问题	答案
岩浆形成的主要过程有哪些？	温度升高、压力降低以及水的加入。

接下来，我们需要对每个过程进行详细解释。关于温度升高导致岩石熔化这一点，我们无需多作解释：

问题	答案
为什么压力降低会导致岩石熔化？	因为岩石中的原子获得了更大的运动自由度
为什么加入水会降低岩石的熔点？	因为水分子会破坏岩石矿物中的化学键

第三：岩浆形成的地点。我们同样将地点列表与具体细节分开：

Question	Answer
岩浆主要在哪些地方形成？	地幔热点区域、地壳裂谷带和板块俯冲带。

然后我们深入探讨细节。对于每个岩浆形成的地点，我们需要了解其中涉及的具体过程，以及完整的因果关系。同时，我们还会反过来思考：哪些地质环境涉及了特定的岩浆形成过程。

问题	答案
热点区域的岩浆形成过程是什么？	减压熔融。
裂谷带的岩浆形成过程是什么？	减压熔融。
俯冲带的岩浆形成过程是什么？	温度升高和水分增加。
哪些地质环境下会因压力释放而形成岩浆？	热点和裂谷带。
哪些地质环境下会因温度升高和水分增加而形成岩浆？	俯冲带。
热点地区的岩浆是如何形成的？	当高温地幔物质上涌时，压力降低导致其发生熔融。
裂谷带的岩浆是如何形成的？	当板块分离时，高温岩石上涌填充裂隙，压力降低导致其发生熔融。
俯冲带的岩浆是如何形成的？	含水的地壳俯冲到地幔中，水转化为蒸汽并上升，水分的加入使上覆岩石发生熔融。

我们可以这样可视化所得到的知识图谱：

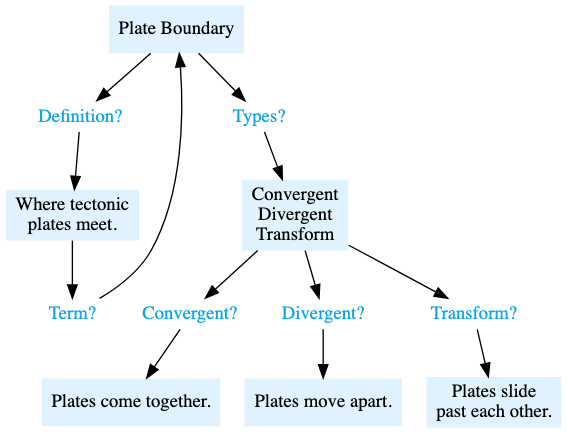
示例：板块构造理论

以下是关键信息：

——————

地球表面的地壳板块在相互接触的区域形成「板块边界」。板块边界可以分为三种类型：

汇聚型边界：两个板块相互靠近并发生碰撞。
离散型边界：两个板块相互分离，向相反方向移动。
转换型边界：两个板块沿着边界平行滑动。

——————

遵循抽认卡双向设计的原则，我们为「板块边界」这一概念制作两张抽认卡：

问题	答案
什么是板块边界？	地壳板块相互接触的区域。
地壳板块相互接触的区域被称为什么？	板块边界。

关于不同类型的板块边界，我们只需从概念到具体类型的方向提问（无需问「什么是转换型边界？」因为名称本身已经揭示了其性质）：

问题	答案
板块边界有哪几种类型？	汇聚型边界、离散型边界和转换型边界。

对于每种类型的板块边界，我们同样采用两种提问方式：

问题	答案
定义：汇聚型边界	构造板块相互靠近并碰撞的区域。
定义：离散型边界	构造板块相互远离的区域。
定义：转换型边界	构造板块沿着边界相对滑动的区域。
构造板块相互靠近的地质现象称为什么？	汇聚型边界。
构造板块相互远离的地质现象称为什么？	离散型边界。
构造板块相对滑动的地质现象称为什么？	转换型边界。

图示展现了这些问题如何在知识图谱中连接各个概念：

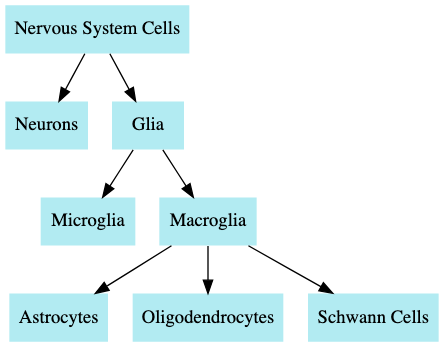
示例：神经细胞

——————

神经系统中的细胞主要分为两类：神经元和神经胶质细胞。神经胶质细胞可进一步分为大胶质细胞和小胶质细胞。其中，大胶质细胞又包括三种类型：星形胶质细胞、少突胶质细胞和施万细胞。

——————

这种结构可以通过以下图示直观地呈现：

基于这种层级结构，我们可以设计一些由上至下的问题：

问题	答案
神经系统由哪些类型的细胞构成？	神经元和胶质细胞。
胶质细胞可以分为哪些类型？	小胶质细胞和大胶质细胞。
大胶质细胞包括哪些类型？	星形胶质细胞、少突胶质细胞和施万细胞。

以下是一些自下而上的问题。当答案明显时，我们通常不会问这些问题。例如，「小胶质细胞/大胶质细胞属于什么类型」这个问题的答案是显而易见的。

问题	答案
星形胶质细胞属于哪一类？	大胶质细胞。
少突胶质细胞属于哪一类？	大胶质细胞。
施万细胞属于哪一类？	大胶质细胞。

示例：神经元类型

这是一个简短的例子，说明如何保持卡片内容简洁，并使用层级结构来分解复杂信息。

以下是我的神经科学笔记摘录：

——————

神经元可以根据其功能分为三类：

感觉神经元：将感觉信息传入大脑。
运动神经元：向肌肉发送运动指令。
中间神经元：在中枢神经系统内部进行连接。这类神经元可进一步分为：

局部：与周围神经元形成局部回路。
中继：具有长轴突，负责在不同脑区之间传递信息。

——————

让我们先从一个错误的示范开始，即在一张卡片中塞入过多信息。

问题	答案
神经元的功能类别有哪些?	感觉神经元：负责将感觉信息传入大脑。运动神经元：负责向肌肉发送运动指令。中间神经元：负责在中枢神经系统内部进行连接。（太长了）
中间神经元有哪些不同类型?	局部：与附近的神经元形成神经回路。中继：具有较长的轴突，负责不同脑区之间的信息传递。（太长了）

现在，让我们将术语与定义分开：

问题	答案
神经元可以分为哪几类主要功能类型？	感觉、运动和中间。
感觉神经元的主要功能是什么？	将外界环境的信息传入大脑的神经元。
运动神经元的主要作用是什么？	将大脑的指令传递给肌肉的神经元。
中间神经元在神经系统中扮演什么角色？	在中枢神经系统内部进行信息传递和处理的神经元。
中间神经元可以细分为哪两种类型？	局部和中继。
局部中间神经元的主要特征是什么？	与附近的神经元形成局部神经回路的中间神经元。
中继中间神经元的关键特点是什么？	具有较长的轴突，能够在不同脑区之间传递信息的中间神经元。

现在我们进行反向提问：请根据给出的定义回答相应的神经科学术语。

问题	答案
将信息传入大脑的神经元称为什么？	感觉神经元。
向肌肉发送指令的神经元称为什么？	运动神经元。
在中枢神经系统内部相互连接的神经元称为什么？	中间神经元。
与周围神经元形成局部回路的中间神经元称为什么？	局部中间神经元。
在大脑不同区域之间传递信息的中间神经元称为什么？	中继中间神经元。

示例：向量空间

以下是我们将要学习的内容：

——————

简单来说，向量空间是一个集合，其中的元素称为向量，这些向量可以进行加法运算和数乘运算。

更严格的数学定义是：在数域 $\mathbb{F}$ 上的向量空间是一个集合 $V$ ，以及两种运算：

向量加法： $V \times V \to V$
标量乘法： $V \times \mathbb{F} \to V$

这两种运算需要满足以下公理：

加法交换律

$u + v = v + u$

加法结合律

$u + (v + w) = (u + v) + w$

加法单位元

$\exists 0 \in V : v + 0 = v$

加法逆元

$\forall v \in V, \exists -v \in V : v + (-v) = 0$

标量乘法单位元

$1v = v$

分配律

$\forall v \in V, a,b \in \mathbb{F} : (a+b)v = av + bv$

——————

我们需要将其分解。让我们一步一步来。

首先，我们要区分非正式（直观）定义和正式定义：

问题	答案
简单来说，什么是向量空间？	向量空间是一个数学概念，它描述了一个包含特定元素（称为向量）的集合。这些向量可以相互相加，也可以被数字（称为标量）放大或缩小。
从数学角度严格定义，什么是向量空间？	在数学中，向量空间是指在某个数域 $\mathbb{F}$ 上定义的一个集合 $V$，其配备了两种基本运算：向量加法和标量乘法。

我们添加了一个关于符号的简短问题（你可以选择跳过这个问题，这是一个示例）：

问题	答案
向量空间的元素叫什么？	向量。

关于运算符号的问题：

问题	答案
向量加法运算的数学表示是什么？	$V \times V \to V$
标量乘法运算的数学表示是什么？	$V \times \mathbb{F} \to V$

关于公理的问题：

问题	答案
定义向量空间的基本公理有哪些？	1. 加法交换律 2. 加法结合律 3. 加法单位元 4. 加法逆元 5. 标量乘法的单位元 6. 分配律

最后，让我们来询问每个公理的具体含义：

问题	答案
向量空间公理：加法交换律	$u + v = v + u$
向量空间公理：加法结合律	$u + (v + w) = (u + v) + w$
向量空间公理：加法零元	$\exists 0 \in V : v + 0 = v$
向量空间公理：加法逆元	$\forall v \in V, \exists -v \in V : v + (-v) = 0$
向量空间公理：标量乘法的单位元	$1v = v$
向量空间公理：分配律	$\forall v \in V, a,b \in \mathbb{F} : (a+b)v = av + bv$

下图可以帮助你直观地理解这些抽认卡及其之间的关系：

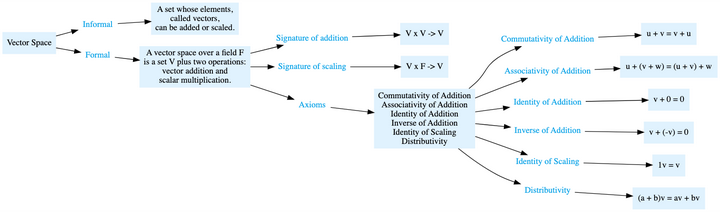
为了更全面地掌握这些概念，你还可以创建反向问题：

问题	答案
什么是允许其元素进行加法和数乘运算的集合？	向量空间
请给出这个公理的名称：$u + v = v + u$	加法交换律
请给出这个公理的名称：$u + (v + w) = (u + v) + w$	加法结合律
请给出这个公理的名称：$\exists 0 \in V : v + 0 = v$	加法单位元
请给出这个公理的名称：$\forall v \in V, \exists -v \in V : v + (-v) = 0$	加法逆元
请给出这个公理的名称：1v=v	标量乘法的单位元
请给出这个公理的名称：$\forall v \in V, a,b \in \mathbb{F} : (a+b)v = av + bv$	分配律

示例：奇偶群

——————

奇偶群是一个简单而富有洞察力的群论例子，它描述了偶数和奇数相加的规律。该群的基础集合为{偶，奇}，其中「偶」表示所有偶数，「奇」表示所有奇数。群的运算表如下：

+	偶	奇
偶	偶	奇
奇	奇	偶

「偶」是单位元。这个群是阿贝尔群。

——————

我们可以创建相应的抽认卡：

问题	答案
什么是奇偶群？	一个描述偶数和奇数加法规则的群。
奇偶群的阶是多少？	2
奇偶群的基础集合是什么？	{偶,奇}
奇偶群的单位元是什么？	偶
奇偶群的运算是什么？	基于偶数和奇数的加法规则
偶 + 偶 =	偶
偶 + 奇 =	奇
奇 + 偶 =	奇
奇 + 奇 =	偶
奇偶群是否为阿贝尔群？为什么？	是的，因为满足加法交换律。

示例：逻辑后果

摘自我的逻辑学笔记：

——————

逻辑后果的两个概念是：

语义后果：如果在所有使 $P$ 为真的解释中， $Q$ 也必定为真，那么 $Q$ 是 $P$ 的语义后果。这种关系用符号 $P \models Q$ 表示。
句法后果：如果存在一个从 $P$ 到 $Q$ 的证明，那么 $Q$ 是 $P$ 的句法后果。这种关系用符号 $P \vdash Q$ 表示。

简而言之，语义后果关注的是命题在各种可能解释下的真值关系，而句法后果则聚焦于命题之间的形式化推理过程。

——————

让我们从最基本的问题入手：

问题	答案
逻辑后果的两个核心概念是什么？	语义后果和句法后果。

接下来，我们将深入探讨与语义后果相关的具体问题：

问题	答案
请定义语义后果。	如果在所有使 $P$ 为真的解释中，$Q$ 也必定为真，那么 $Q$ 是 $P$ 的语义后果。
用什么符号表示「$Q$ 是 $P$ 的语义后果」？	$P \models Q$
$P \models Q$ 表达了什么意思？	$Q$ 是 $P$ 的语义后果
语义后果是通过什么来连接句子的？	解释。
在逻辑后果的概念中，哪一种涉及到解释？	语义后果。

然后是句法结果：

问题	答案
请定义句法后果	如果存在一个从 $P$ 到 $Q$ 的证明，那么 $Q$ 是 $P$ 的句法后果。
用什么符号表示「$Q$ 是 $P$ 的句法后果」？	$P \vdash Q$
$P \vdash Q$ 表达了什么意思？	$Q$ 是 $P$ 的句法后果
句法后果是通过什么来连接句子的？	证明。
在逻辑后果的概念中，哪一种涉及到证明？	句法后果。

示例：时期划分

时间线是一个绝佳的例子，展示了如何通过层次化分解信息来帮助我们学习长序列。有时这种分解工作已经为我们事先完成了。

——————

地质年代表（GTS）将地球的地质历史记录划分为四个相互嵌套的时间单位：

宙是最大的时间单位，每个宙持续数亿年之久。
宙进一步细分为若干个代，每个代的持续时间从数千万年到数亿年不等。
代再往下划分为纪，每个纪的时间跨度从数百万年到数千万年不等。
最后，纪被细分为世，每个世持续数十万年到数百万年。

地球历史上的四个宙，按从最古老到最近的顺序排列如下：

冥古宙（从 45 亿年前到 40 亿年前）
太古宙（从 40 亿年前到 25 亿年前）
元古宙（从 25 亿年前到 5.38 亿年前）
显生宙（从 5.38 亿年前持续至今）

——————

我们需要了解以下三个方面：

地质年代表的定义。
地质年代表如何划分地球的历史。
地球历史中的四个宙。

让我们从最基本的概念入手，即地质年代表的定义：

问题	答案
地质年代表是什么？	地球历史的时间线。
地球历史的时间线被称为什么？	地质年代表。

地质时间单位按从大到小的顺序排列为：宙、代、纪、世。我们可以使用序列脚本来生成相关的学习卡片。以下是输入数据：

地质时间单位
宙
代
纪
世

运行 cat units.txt | ./sequence.py > units.csv，然后将 units.csv 导入到Mochi，我们就能得到这些抽认卡：

问题	答案
地质时间单位：请按从大到小的顺序列出所有单位	宙、代、纪、世。
地质时间单位：最大的时间单位是什么？	宙。
地质时间单位：第二大的时间单位是什么？	代。
地质时间单位：第三大的时间单位是什么？	纪。
地质时间单位：最小的时间单位是什么？	世。
地质时间单位：宙在序列中排第几？	1。
地质时间单位：代在序列中排第几？	2。
地质时间单位：纪在序列中排第几？	3。
地质时间单位：世在序列中排第几？	4。
地质时间单位：宙的下一级单位是什么？	代。
地质时间单位：代的下一级单位是什么？	纪。
地质时间单位：纪的下一级单位是什么？	世。
地质时间单位：代的上一级单位是什么？	宙。
地质时间单位：纪的上一级单位是什么？	代。
地质时间单位：世的上一级单位是什么？	纪。

其实你不需要全部都记。以下几张可能就足够了：

问题	答案
地质年代单位的层级是什么，从大到小排列？	宙、代、纪、世。
地质年代中最大的时间单位是什么？	宙。
地质年代中第二大的时间单位是什么？	代。
地质年代中第三大的时间单位是什么？	纪。
地质年代中最小的时间单位是什么？	世。

既然这是一个概念层级结构，我们还需要了解每个单位的定义：

问题	答案
什么是宙？	地质年代划分的一个单位。
什么是代？	地质年代划分的一个单位。
什么是纪？	地质年代划分的一个单位。
什么是世？	地质年代划分的一个单位。

另外，由于每个单位都有其持续时间，我们还需要了解它们的时间跨度。这个问题可以从正反两个方向来提出：

问题	答案
一个宙的持续时间是多久？	数亿年。
哪个地质年代单位持续数亿年？	宙。
一个代的持续时间是多久？	数千万至数亿年。
哪个地质年代单位持续数千万至数亿年？	代。
一个纪的持续时间是多久？	数百万至数千万年。
哪个地质年代单位持续数百万至数千万年？	纪。
一个世的持续时间是多久？	数十万至数百万年。
哪个地质年代单位持续数十万至数百万年？	世。

接下来我们将讨论四个宙。这些宙构成了一个序列，我们不会再完整地走完整个流程，因为你可能已经再次使用了这些：

问题	答案
请按从最古老到最新的顺序列出地球历史的宙	冥古宙、太古宙、元古宙、显生宙
第一个宙是什么？	冥古宙
第二个宙是什么？	太古宙
第三个宙是什么？	元古宙
第四个宙是什么？	显生宙

我们也会问每个宙的开始和结束，前驱和后继：

问题	答案
冥古宙从何时开始？	45 亿年前
冥古宙在何时结束？	40 亿年前
哪个宙开始于 45 亿年前？	冥古宙
哪个宙结束于 40 亿年前？	冥古宙
太古宙的起始时间是？	40 亿年前
太古宙的终止时间是？	25 亿年前
40 亿年前开始的是哪个宙？	太古宙
25 亿年前结束的是哪个宙？	太古宙
元古宙从何时开始？	25 亿年前
元古宙在何时结束？	5.38 亿年前
25 亿年前开始的是哪个宙？	元古宙
5.38 亿年前结束的是哪个宙？	元古宙
显生宙的开始时间是？	5.38 亿年前
显生宙何时结束？	现在（仍在持续）
5.38亿年前开始的是哪个宙？	显生宙
目前仍在持续的宙是哪一个？	显生宙

示例：有理数

让我们将这个概念提交到间隔重复中：

——————

有理数集合，用符号 $\mathbb{Q}$ 表示，是所有可以表示为分数形式的数的集合，其中分子和分母都是整数，且分母不能为零。

用数学语言严格定义如下：

$\mathbb{Q} = \left\{\, \frac{p}{q} \,\, \middle| \,\, p, q \in \mathbb{Z} \land q \neq 0 \,\right\}$

这里的 $\mathbb{Q}$ 代表「商」(quotient)。

——————

在设计抽认卡时，我们可以通过概念图来直观地展示学习内容。首先，我们从核心概念——有理数开始：

接着，我们添加一个表示符号的节点，并通过两个相互关联的问题将其连接：

问题	答案
有理数集合的数学符号是什么？	$\mathbb{Q}$
数学符号 $\mathbb{Q}$ 表示什么？	有理数集合

最后，我们可以加入有理数的严格定义和通俗解释：

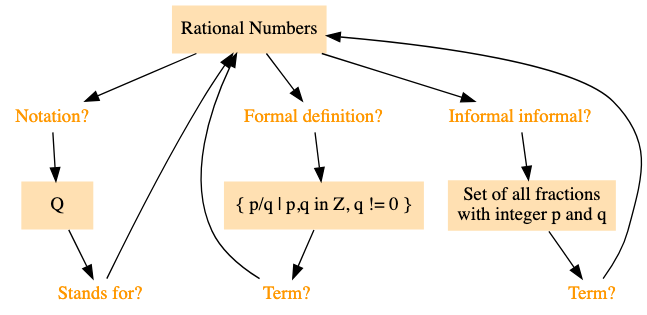
问题	答案
通俗地说，有理数集是什么？	有理数集是由所有可以表示为分数形式的数组成的集合，其中分子和分母都是整数，且分母不为零。
数学上严格定义，有理数集是什么？	$$\mathbb{Q} = \left{\, \frac{p}{q} \,\, \middle
整数之间的比值构成的集合在数学中称为什么？	有理数集。
集合 $$\left\{\, \frac{p}{q} \,\, \middle\| \,\, p, q \in \Z \land q \neq 0 \,\right\}$$ 在数学中表示什么？	有理数集。

关于数学符号的补充说明：$\mathbb{Q}$ 在表示有理数集时的含义：

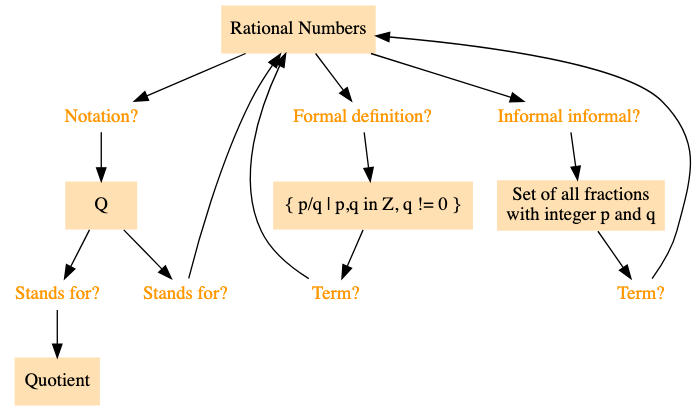
问题	答案
在数学中，为什么用 $\mathbb{Q}$ 来表示有理数集？	Q 代表英文单词「quotient」(商)

示例：正则表达式

这个例子展示了如何通过两种方式提问。

以下问答卡片展示了从概念到具体正则表达式语法的对应关系：

问题	答案
在正则表达式中，用什么符号匹配一行文本的开头？	^
在正则表达式中，用什么符号匹配一行文本的结尾？	$
在正则表达式中，用什么模式匹配任意单个数字？	\d

除上述内容外，还可添加从正则表达式到概念的卡片：

问题	答案
^ 匹配什么？	行的开始
$ 匹配什么？	行的结束
\d 匹配什么？	0 到 9 之间的任意数字

示例：电压

这是一个展示如何以不同方式提问的范例。

——————

$A$ 和 $B$ 两点之间的电压可以通过以下两种方式定义：

两点之间的电势差。
电荷量为 $1C$ 的粒子从 $A$ 点移动到 $B$ 点所做的功。

——————

这里的思路是：

首先，我们从电势差和功两个角度来询问电压的定义。
其次，我们还要询问每个定义所对应的专业术语。

据此，我们可以制作出以下抽认卡：

问题	答案
从电势的角度来看，电压是什么？	两点之间的电势差。
从功的角度来看，电压是什么？	单位电荷（1 库仑）从一点移动到另一点所做的功。
两点之间的电势差通常称为什么？	电压。
单位电荷在两点之间移动所做的功通常称为什么？	电压。

示例：同分异构体

——————

当两种化合物具有相同的化学式（即各元素的原子数相同），但三维结构不同时，我们称这两种化合物互为同分异构体。

异构体可以分为以下几类：

结构异构体：指分子式相同但原子连接方式不同的化合物。
立体异构体：指分子式和化学键相同，但空间排列不同的化合物。立体异构体可以进一步分为：

构象异构体：可以通过单键旋转相互转化的异构体。
构型异构体：不能通过单键旋转相互转化，必须打断化学键才能转化的异构体。构型异构体又可细分为：

对映异构体：互为不能重合的镜像的一对异构体。由于它们对平面偏振光的旋转方向不同，也被称为光学异构体。
非对映异构体：不是对映异构体的立体异构体。其中一个重要的类型是：

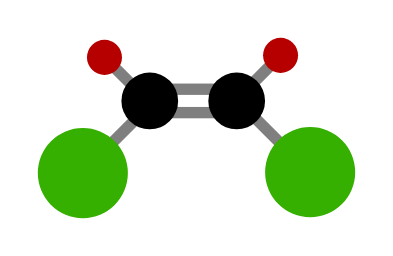
顺式/反式异构体：在具有刚性结构的分子中，当两个官能团可能处于同侧或异侧时形成的异构体。当两个官能团位于刚性结构的同一侧时，称为顺式异构体；当它们位于相对的两侧时，称为反式异构体。

下图展示了一个顺式异构体的例子：

下图展示了一个反式异构体的例子：

——————

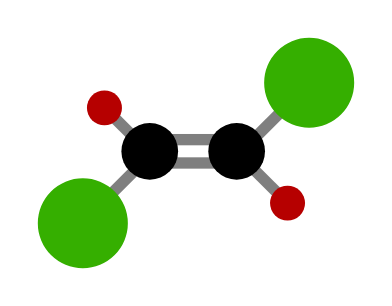
这个概念体系相对简单明了：我们需要学习一个定义的层次结构。我们可以将学习任务分为两个部分：

首先，掌握定义。练习从术语到定义，以及从定义到术语的互相转换。
其次，理解层次结构：学习各种异构体的类型和亚类型之间的关系。

让我们从定义开始。首先我们按照正向顺序提出问题：

问题	答案
什么是异构体？	当两种化合物具有相同分子式但三维结构不同，它们互为异构体。
什么是结构异构体？	具有相同分子式，但原子之间的连接顺序或方式不同的化合物。
什么是立体异构体？	分子式和化学键连接方式完全相同，但原子在三维空间中的排列不同的化合物。
什么是构象异构体？	可以通过单键周围的自由旋转相互转化的异构体。
什么是构型异构体？	必须打断化学键才能相互转化的异构体。
什么是对映异构体？	互为镜像但不能重合。
什么是非对映异构体？	属于立体异构体但不是对映异构体。
什么是顺反异构体？	两个官能团可以位于刚性结构同侧（顺式）或异侧（反式）的异构体。

然后是反向定义：

问题	答案
分子式相同但三维结构不同的化合物，称为什么？	异构体
分子式相同但化学键连接方式不同的异构体，称为什么？	结构异构体
化学键连接相同但空间排列不同的异构体，称为什么？	立体异构体
可通过单键自由旋转相互转化的异构体，称为什么？	构象异构体
需要断键才能相互转化的异构体，称为什么？	构型异构体
与镜像不能重合的异构体，称为什么？	对映异构体
属于立体异构体但不是对映异构体，称为什么？	非对映异构体
官能团位于刚性结构同侧或异侧的异构体，称为什么？	顺式/反式异构体

为了保持每个知识点的独立性，我们省略了一些信息。现在需要提出问题来回忆那些被省略的信息：

问题	答案
对映异构体的另一个专业术语是什么？	光学异构体。
为什么对映异构体也被称为光学异构体？	这是由于它们能够旋转平面偏振光的特性。
光学异构体是指什么？	这是对映异构体的另一种专业表述。
什么是顺式异构体？	两个官能团位于刚性结构同一侧的异构体。
当一个异构体的两个官能团位于刚性结构的同一侧时，称为什么？	顺式异构体。
什么是反式异构体？	两个官能团位于刚性结构相对两侧的异构体。
当一个异构体的两个官能团位于刚性结构的相对两侧时，称为什么？	反式异构体。

现在，我们来探讨这些概念在化学分类体系中的层级关系。我们首先从概念的层级结构出发，从上层概念到下层概念进行提问：

问题	答案
异构体可以分为哪两大类？	结构异构体和立体异构体。
立体异构体又可以细分为哪两类？	构象异构体和构型异构体。
构型异构体包括哪两种？	对映异构体和非对映异构体。
非对映异构体中最常见的是哪种？	顺式/反式异构体。

然后从下层到上层：

问题	答案
结构异构体属于？	异构体
立体异构体属于？	异构体
构象异构体属于？	立体异构体
构型异构体属于？	立体异构体
对映异构体属于？	构型异构体
非对映异构体属于？	构型异构体
顺式/反式异构体属于？	非对映异构体

最后，举几个例子：

问题	答案
下图所示的是哪种异构体？	顺式异构体
下图所示的是哪种异构体？	反式异构体

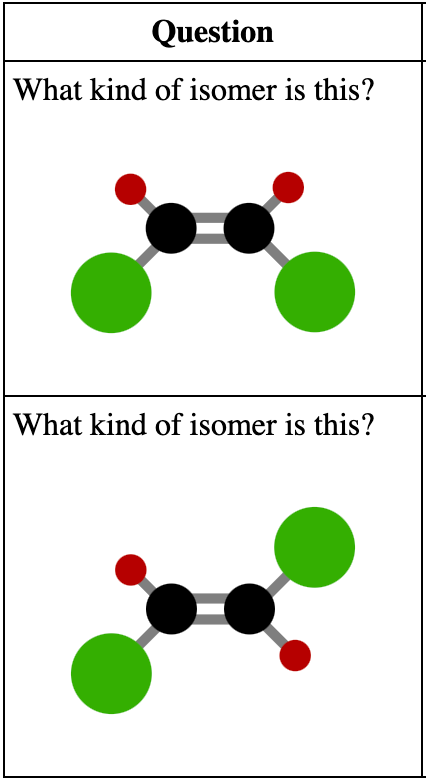
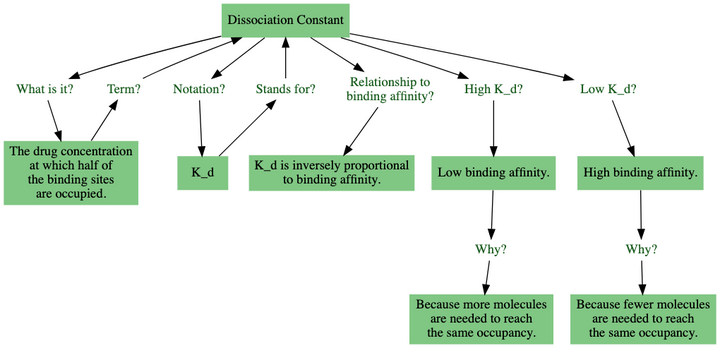
示例：药理学

——————

药物的解离常数（ $K_d$ ）是指在实验中，当一半的结合位点被药物分子占据时所对应的药物浓度。

——————

这个例子展示了如何缓存你的见解。从这段描述中，我们可以进一步推导出：

当 $K_d$ 值较高时，表明药物对结合位点的亲和力低，这是因为需要更高的药物浓度才能达到相同的结合程度。
相反，当 $K_d$ 值较低时，意味着药物对结合位点的亲和力高，因为只需较低的浓度就能实现相同的占有率。

根据上述两点，我们还可以得出一个重要结论：

$K_d$ 与结合亲和力成反比关系。

基于这些信息，我们可以提出一系列问题：

问题	答案
药物占据一半结合位点时的浓度，其专业术语是什么？	解离常数。
解离常数通常用什么符号表示？	$K_d$
$K_d$ 代表什么？	解离常数。
$K_d$ 值较低意味着什么？	药物具有高结合亲和力。
为什么 $K_d$ 值低能反映出高结合亲和力？	因为较少的药物分子就能达到相同的占有率。
$K_d$ 值较高代表什么？	药物具有低结合亲和力。
为什么 $K_d$ 值高表明结合亲和力低？	因为需要更多的药物分子才能达到相同的占有率。
如果已知药物的结合亲和力高，这说明其 $K_d$ 值如何？	$K_d$ 值较低。
反之，若药物的结合亲和力低，其 $K_d$ 值会如何？	$K_d$ 值较高。
请描述 $K_d$ 与结合亲和力之间的关系。	$K_d$ 与结合亲和力成反比。
$K_d$ 与结合亲和力成比例关系。	反。