第二十九章间隔重复的技术深度剖析

注：本章将展开阐述在第十八章^[1]中引入的概念。

⠀⠀⠀摘要：Math Academy 采用了一种创新的间隔重复算法——部分隐式重复（Fractional Implicit Repetition, FIRe），用于计算学生的学习特征曲线。FIRe 将间隔重复的概念扩展到分层知识结构中，使得在高级主题上的重复能够隐式地涓滴到相关的基础主题中。该算法能够处理部分包含关系，并通过部分包含关系扩展重复流，从而优化学习效果的分配。间隔重复过程的速度会针对每个学生在每个特定主题上进行个性化调整，其中学生的能力和主题的难度是两个相互制约的调整因素。

部分隐式重复（FIRe）

为了计算学生的间隔重复学习特征曲线，Math Academy 采用了一种新兴的间隔重复算法，名为部分隐式重复（Fractional Implicit Repetition, FIRe）。FIRe 将传统的间隔重复扩展到具有层级结构的知识体系中，在这个算法中：

高级主题的重复练习会通过知识间的包含关系，隐式「涓滴」到相关的基础主题，并且
频繁获得隐式重复的基础主题会适当降低这些重复的权重（因为它们通常发生得过早，在效果上不能完全算作下一次重复）。

| 具体实例

让我们用一个具体例子来阐述这个概念。请回想一下，「两位数乘一位数」这个技能实际上包含了「一位数相乘」和「一位数加两位数」这两个基础技能。

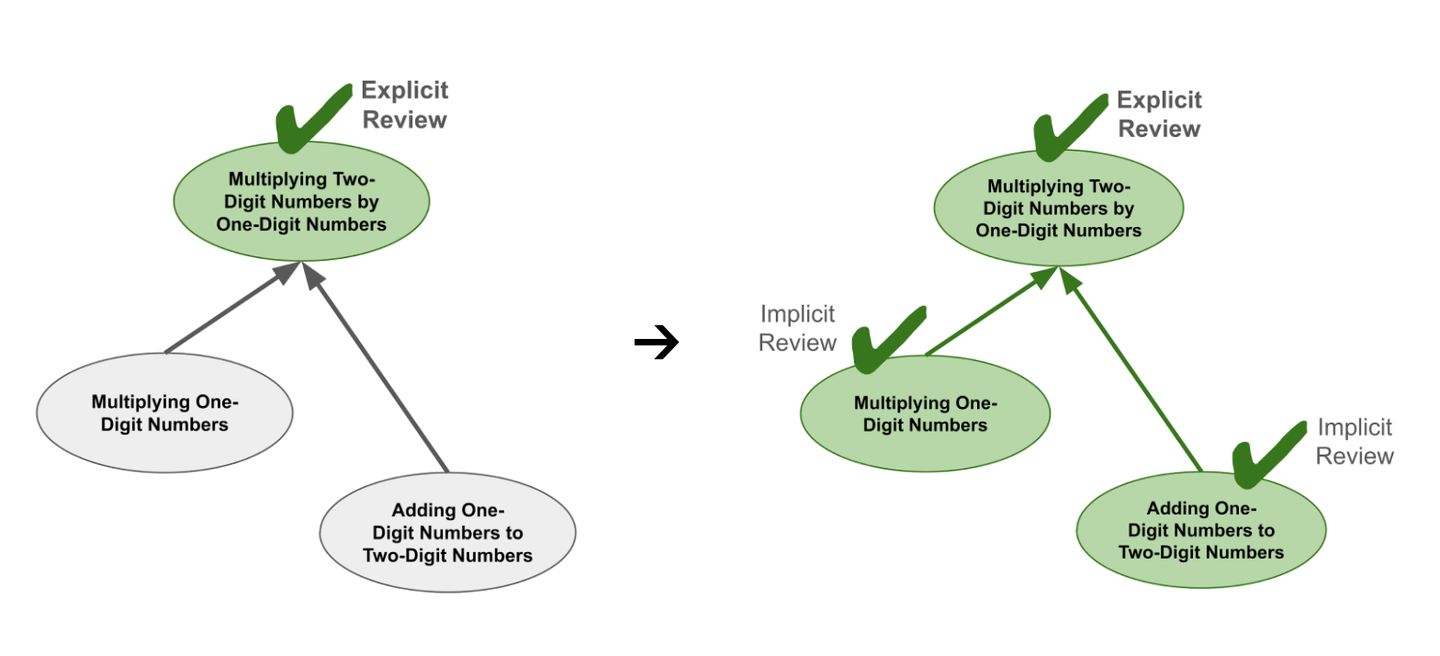
假设你成功通过了「两位数乘一位数」的重复练习，这次成功的练习不仅仅针对这一特定技能，它还会回顾「一位数相乘」和「一位数加两位数」这两个基础技能。这是因为你刚刚证明了你仍然熟练掌握这些基础技能。

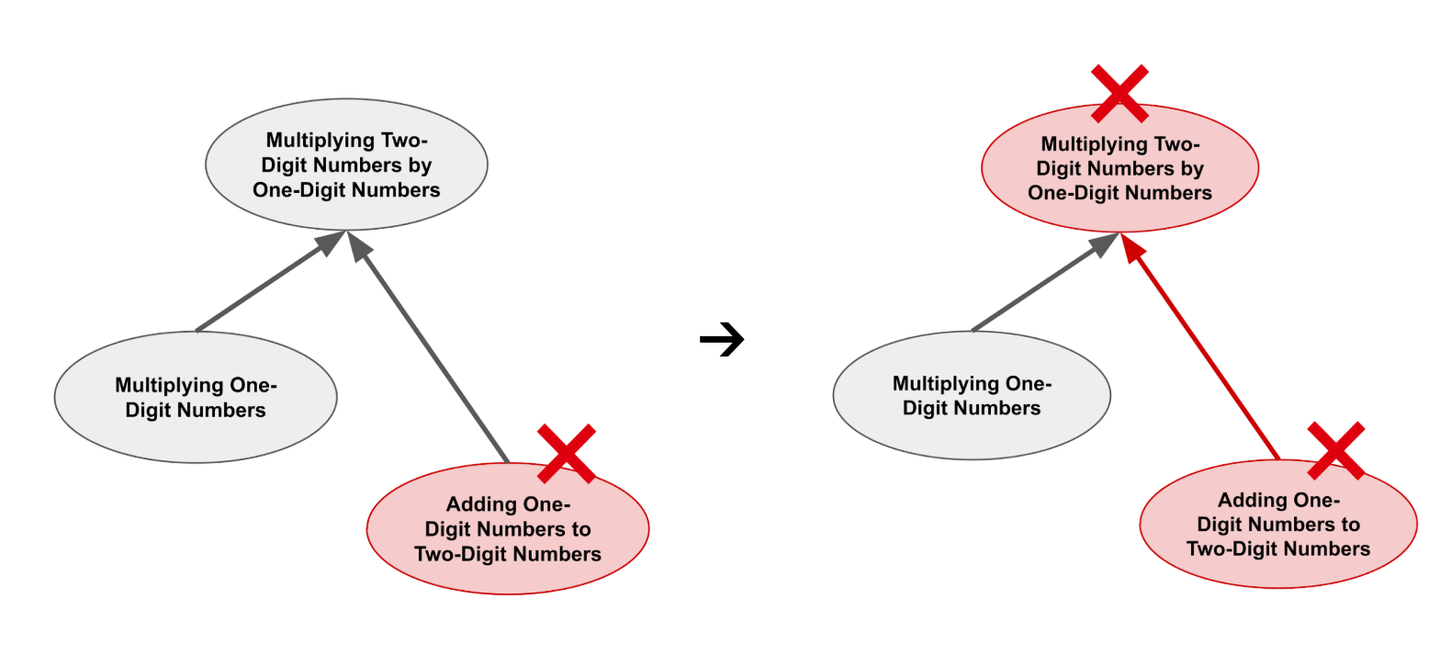
相反，如果你在「一位数加两位数」的重复练习中失败了，这次失败不仅影响这个特定技能，还会「连带影响」到「两位数乘一位数」这个更复杂的技能。毕竟，如果你连一位数加两位数都做不到，你就更不可能完成两位数乘一位数的计算了。同理，如果你在「一位数相乘」的重复练习中失败，也会产生类似的连锁反应。

| 重复流的可视化

需要注意的是，重复流（repetition flows）可以延伸很多层——不仅仅是直接包含的主题，还有被包含主题所包含的「二阶」主题，然后是被二阶主题包含的三阶主题，以此类推。

在视觉上，得分（credit）像闪电一样向下流经知识图。

罚分（penalty）像生长的树木一样向上流经知识图。

| 部分包含

FIRe 还自然地处理部分包含的情况，在这种情况下，一个较简单主题只有某些部分在一个高级主题中被隐式练习。这在更高等的数学中更常见。

例如，在微积分中，高级积分技巧如分部积分要求你计算各种数学函数的积分，如多项式、指数函数和三角函数。但其中一些函数可能只出现在分部积分问题的一部分中。所以，如果你完成了一次分部积分的重复练习，你应该只获得对每个部分包含主题的一部分重复练习。

下图中，我们用数字权重标注主题间的包含关系，表示学习高级主题时涉及各个基础主题的程度。你可以将每个权重理解为：从高级主题中随机选取一个问题时，它包含某个基础主题内容的概率。

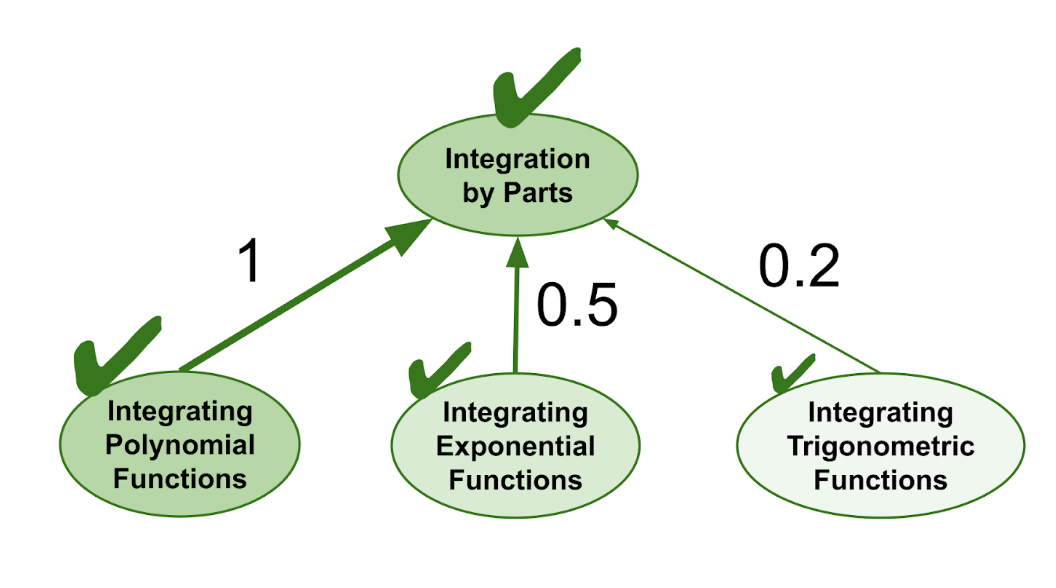
FIRe 通过这种部分包含，将重复流延伸到多个层级。最终结果是：

重复练习沿着完全包含关系构成的「主干」畅通无阻地传递，
同时沿着从主干分支出去的部分包含关系逐渐衰减。

手动设置包含权重

| 直接且关键的前置知识就足够了

由于包含权重需要手动设置，为知识图谱中每对主题都设置明确的权重是不切实际的。我们的系统包含数千个主题，如果列出所有可能的主题对，权重矩阵将包含数千万个条目。那么，我们该如何设置这些庞大的权重数据呢？

事实上，我们并不需要明确设置矩阵中的每一个权重。只需要为满足以下条件的主题对设置权重即可：

权重有一个非零的值，
无法通过重复流推断出权重，
两个主题在前置知识图中的距离较近。

并且我们假定，除了在重复流中隐式计算得出的权重外，其他所有权重均为零。这一假设基于以下理由：

权重的大小反映了隐式重复所产生的学习效果。为了使隐式重复能够有效减少显式复习的需求，它必须与足够显著的学习效果相关联。
如果重复流能够推断出某个权重，那么手动设置该权重通常不会改变结果（除非手动设置是为了纠正重复流可能错误推断的值）。
如果两个主题在前置知识图中相距较远，即使它们之间存在完全包含关系，其权重对减少复习需求的影响也不会太大。这是因为当学生学习到更高级的主题时，他们往往已经在较基础的主题完成了大部分的显式复习。

值得注意的是，满足上述条件的权重通常分布在直接关联和关键的前置知识连接上，而这些连接的数量在规模上与主题总数呈线性关系。这一特点使得手动设置包含权重变得可行：只需为每个直接关联或关键的前置知识分配一个权重即可。

值得注意的是，在知识图谱中，即使某些主题之间的直接关联或关键前置知识的关联强度低至零，也是常见现象。这种情况通常出现在学习某个主题时，学生只需对其前置知识有概念性的理解，而不必精通到能够独立解决相关问题的程度。

| 非祖先包含关系与掌握标准

为了符合课程标准，有时需要在多个课程中设置等效主题，其中高级课程中的等效主题会对低级课程中教授的相同技能进行更深入的处理。然而，这些较简单的等效主题通常不会被要求作为更高级等效主题的前置知识。

例如，基于代数的统计课程和基于微积分的统计课程会有许多涵盖相同技能的等效主题。尽管基于微积分的统计课程会提供这些技能的更高级处理方法，但基于代数的统计课程中相对应的等效主题并不会被视为前置知识。

即使简单的等效主题不会通过直接关联或关键前置知识路径来成为高级等效主题的「祖先」，我们仍然可以在它们之间设置完全包含的权重关系，这样完成高级主题的学生也会自动获得相应简单等效主题的得分。这种关系被称为非祖先包含关系。

非祖先包含关系，结合基于课程的掌握标准（即任何参加该课程的学生被自动视为已掌握的低级课程主题），也可用于为低级课程中的末端主题分配得分。课程的掌握标准包括以下低级课程主题：

那些「足够基础」的主题，可以完全假设学生已经掌握；或
那些位于课程诊断测试中可能评估为最简单主题「之下」的主题。

直观地说，掌握标准的上界标志着判断学生是否有可能参加某门课程的分界线。

学生-主题学习速度

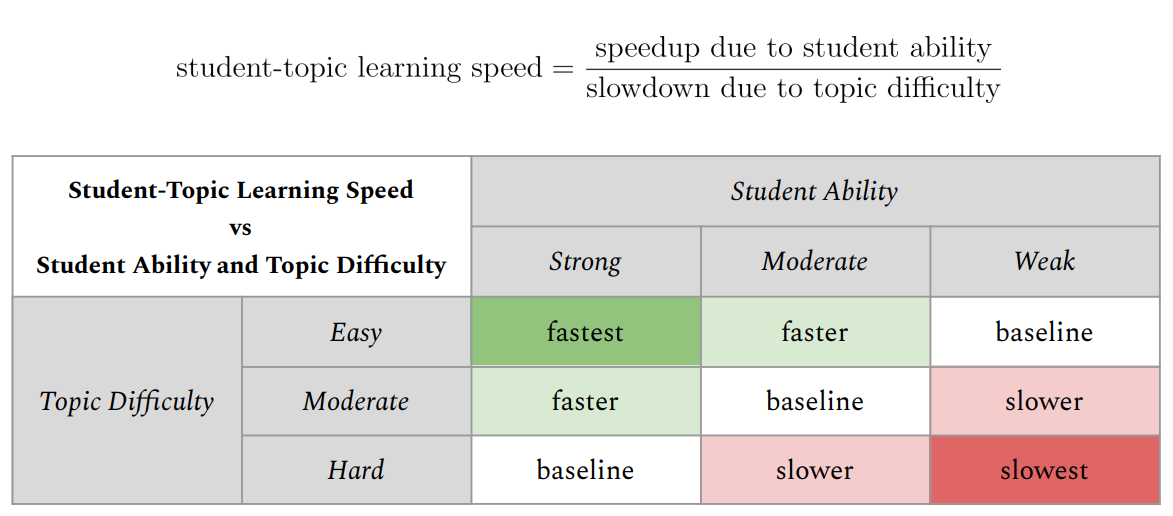
| 学生能力与主题难度的比率关系

学生能力和主题难度是两个相互制衡的因素——较高的学生能力会提升整体学习速度，而较高的主题难度则会降低学习速度。因此，要计算学生在特定主题上的学习速度，我们需要：

计算学生能力带来的加速效应，
计算主题难度导致的减速效应，然后
求出二者的比率。

| 在单个主题层面测量学生能力

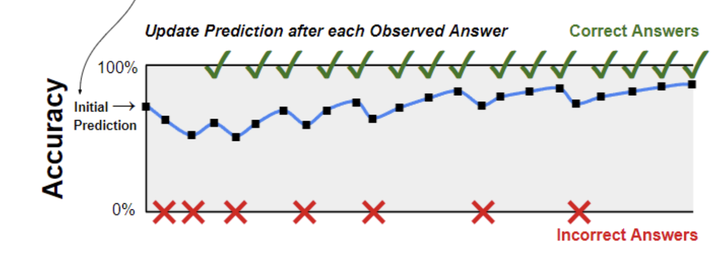
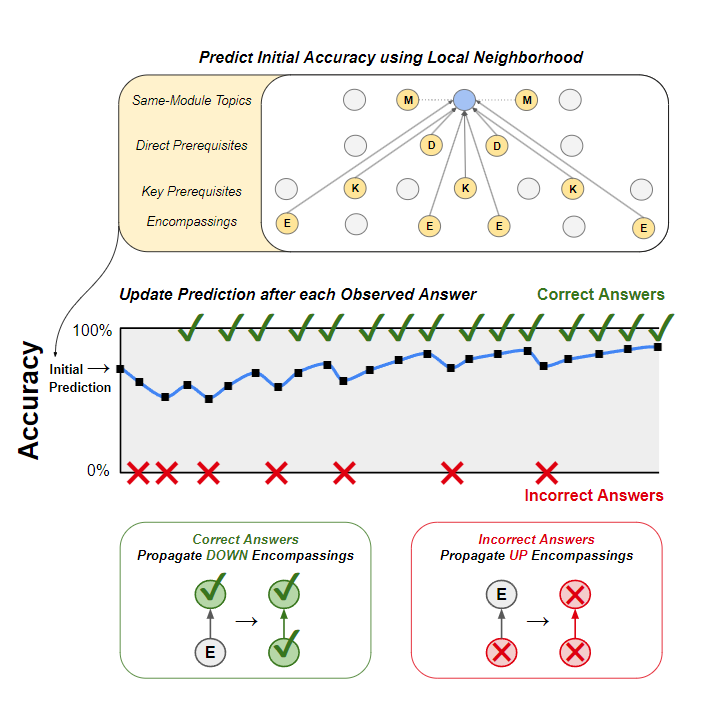
学生能力是在单个具体主题的精细层面上进行测量的——我们会追踪学生答题的准确率，对近期答题结果给予更高权重，并且还会进行能力评估的传播：

将正确答案的影响向下传递至包含在内的更简单的子主题，以及
将错误答案的影响向上传递至包含该主题的更高级主题。

为了确定一个主题准确率的初始值，我们会基于该主题的局部关联网络进行预测，这个网络包括其直接前置知识、关键前置知识、上层包含关系以及同一模块中的相关主题。

| 测量主题难度

主题难度是通过计算所有认真学习的学生在评估中回答该主题相关问题时的整体准确率来测量的。

理论上，如果能够在每个主题上完美精确地测量学生能力，那么就不再需要主题难度这一指标，学生-主题学习速度可以完全基于学生能力来确定。但在实际应用中，依赖主题难度指标仍有两个重要原因：

它能改善初始预测效果。虽然我们已经掌握了特定学生在其他主题上的学习速度信息，但主题难度能提供该特定主题对其他学生的学习速度信息。这是一个独立且信息丰富的信号源。
它自然地起到校正的作用。当主题难度较高时，它会降低学习速度——这是合理的，因为高难度主题通常导致评估表现不佳，而这主要是由于学生没有进行足够的复习所致。同样，当主题难度较低时，它会提高学习速度——这也是合理的，因为低难度主题通常表现为极高的评估成绩，这表明学生可能不需要目前所接受的那么多复习。

宏观结构

从宏观角度看，Math Academy 的间隔重复模型结构可以概括如下：

$\begin{align*} repNum &\to \max \left( 0, \phantom{,} repNum + speed \cdot decay^{\, failed} \cdot netWork \right) \\ memory &\to \max \left( 0, \phantom{,} memory + netWork \right) (0.5)^{ \, days \, / \, interval} \end{align*}$

repNum：学生在特定主题上成功完成的间隔重复轮数。

在以下定义中，「重复」指的是在适当时间进行的成功复习。
days：自上次重复以来经过的天数。
interval：第 repNum 次重复和第 repNum+1 次重复之间的理想间隔天数。
memory（记忆值）：表示学生在距离上次重复一段时间后的记忆保留率期望。记忆值会随时间逐渐衰退，当记忆值降至某个阈值时，就需要进行下一次重复。另外，如果重复的时间过早（记忆值仍然较高），系统会相应降低该次重复的权重。
speed（学习速度）：根据学生在特定主题上的表现来衡量其学习速度。这个参数决定了学生在间隔重复学习过程中进步或退步的快慢。
failed（失败标记）：重复失败记为 1，通过则为 0。
netWork（净效用）：衡量学生在一次重复中产生的实际学习效果。重复通过时，netWork 为正值；失败时为负值。

在成功的重复中，完成质量越高，netWork 的正值就越大；在失败的重复中，表现越差，netWork 的负值就越大。

如果重复比预期间隔提前进行（即 memory 记忆值仍然较高），netWork 的数值会相应减少

注意，在高级主题上的成功练习也会算做对其包含的较简单主题的隐式练习；同样，在较简单主题上的失败也会对以其为基础的更高级主题产生负面影响。
decay（衰减值）：当学生在复习中失败时，此参数表示其在间隔重复学习过程中后退速度与前进速度的比值。

decay 衰减值是一个从 1 开始的正数，它随着重复的时间远远超过理想间隔而增大，即随着记忆严重衰退而增加。

引入衰减值的目的是为了模拟严重的知识衰退现象，例如广为人知的「暑假滑坡」。在这种情况下，上学年末期学习的内容可能在暑假期间被严重遗忘，以至于在新学年开始时需要更频繁地复习，甚至需要完全重新学习。

第二十三章利用认知学习策略需要技术 - 知乎

第二十七章诊断性考试的技术深度剖析 - 知乎

Thoughts Memo 汉化组译制
感谢主要译者 claude-3.5-sonnet，校对Jarrett Ye、白侑
原文：The Math Academy Way: Using the Power of Science to Supercharge Student Learning

参考

1. 第十八章间隔重复（分散练习） ./1895420939283440005.html

专栏：The Math Academy Way

← 返回目录