遗忘曲线

公式

遗忘曲线描述了回忆的概率随时间推移而下降的情况

• 其中：
• R - 回忆概率(记忆的可提取性)
• S - 记忆痕迹的强度(记忆的稳定性)
• t - 时间

解释

在大量的记忆细节中，遗忘曲线的形状将取决于：(1)记忆的复杂性(即从记忆中统一地提取各个知识细节的难度)，(2)记忆的稳定性(即各个细节在记忆中的建立程度)。例如，一组简单的法语单词，在同一天记忆，可能会排列成一条符合上述公式的曲线。那些法语单词的复杂度会很低（因为它们很容易），稳定性也很低（因为它们刚刚学会）。那些法语单词会随着时间的推移，以相同的概率，一个一个地被遗忘。在时间 t 之后，回忆起某个单词的概率将是 R（可提取性），随着时间走向无穷大，回忆概率将接近零。但是，如果将所有的单词再次复习，其稳定性会增加，保留时间会延长。这在间隔重复中使用，以最小化无限期保留记忆的成本。

幂律还是指数

遗忘是指数型的，然而，不同稳定性的遗忘率的叠加将使遗忘遵循幂律。换句话说，当不同复杂性的记忆混合在一起时，遗忘曲线的形状会发生变化，用负幂函数可能会更好地逼近（最初由赫尔曼·艾宾浩斯在1885 年发现^[1]）。绘制不同稳定性记忆的遗忘曲线就不那么有趣了。它可以比作为不同时间生产的不同保质期的产品确定同一个过期日。幂律近似还面临 t=0 点的问题。另一方面，指数遗忘的力量似乎是毁灭性的。幸运的是，对于表述良好的材料^[2]，由于仅经过几次复习就发展出了高记忆稳定性，衰减常数非常低。

由于记忆干扰^[3]的随机性，遗忘是指数性的

更多内容请看：遗忘的指数性

数据

间隔重复软件 SuperMemo 常规收集数据并显示一组取决于记忆稳定性和知识复杂性的遗忘曲线。每个用户和每个知识集合都会被分配一组 400 条的遗忘曲线，用于不同的稳定性和复杂程度的组合。此外，较新的 SuperMemos 还保留了400 条曲线，其中时间由记忆可提取性估计来表示。这种丰富的数据集有助于 SuperMemo 对每个学生的记忆保持一个准确的模型。

用 SuperMemo 收集的曲线实例。

• 异质知识第一次复习的幂律曲线
• 同质知识二轮复习的指数曲线
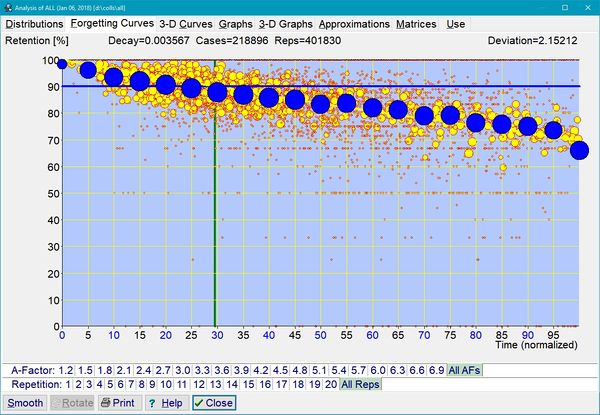
• 不同稳定性和记忆复杂程度的累计归一化曲线（从超过 38 万次重复中提取的 214,000 多个数据点）。
• 不同稳定性水平的 3D 曲线(可提取性对数轴相对于时间反转)

另见

• 艾宾浩斯遗忘曲线的误差^[1]
• 稳定化曲线
• 长期记忆的双组分模型^[4]

例子

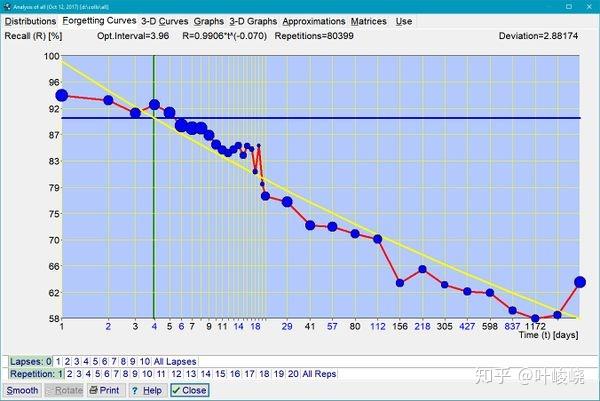
图：用 SuperMemo 收集的新学知识的第一条遗忘曲线。由于学习过程中新鲜引入的学习材料具有异质性，本例采用幂近似。由于缺乏按记忆复杂性的分离，导致不同衰减常数的指数遗忘叠加。在半对数图上，幂律回归曲线呈对数型（黄色），且出现几乎直线。曲线显示，在所提出的案例中，记忆力在 4 年内仅仅下降到 58%，这可以解释为记忆知识在现实生活中的高复用性。在可提取性达到 90% 时，第一个最佳复习间隔是3.96天。遗忘曲线可以用公式 R=0.9906*power(interval, -0.07)来描述，其中 0.9906 为一天后的回忆率，而 -0.07 为衰减常数。在这种情况下，该公式得出 4 天后 90% 的回忆率。80,399 个重复案例被用来绘制所呈现的图表。如果材料中含有较多的难点知识（特别是表述不清的知识^[2]），或者是记忆能力较差的新学生，则会出现更陡峭的记忆力下降。间隔 15-20 的曲线不规则来自于较小的重复样本(对数刻度上较后的间隔类别包含了较宽的间隔范围)

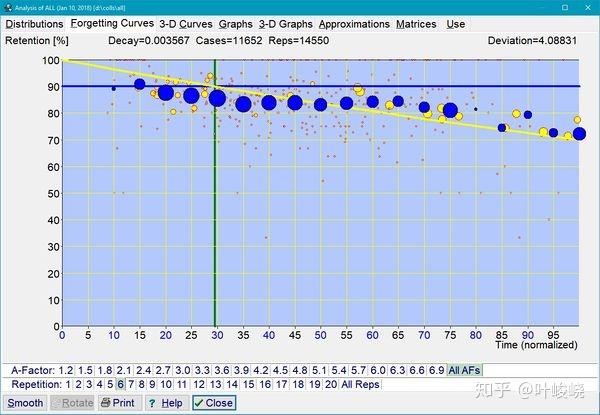
图：SuperMemo 学习材料在相当于第 6 次最佳间隔复习后的指数遗忘曲线。14,550 次的重复已被用来绘制所呈现的图表

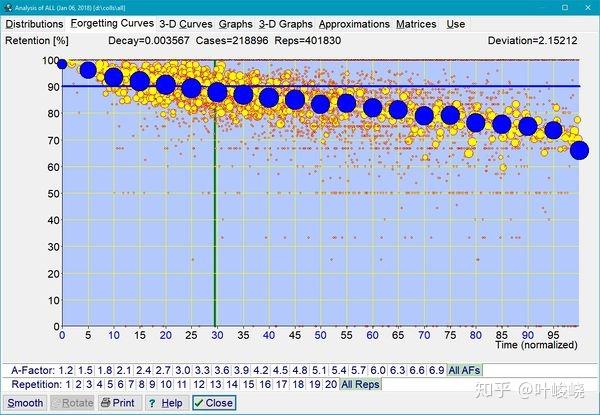
图：混合复杂性和混合稳定性的学习材料的累积遗忘曲线。该图是通过400 条遗忘曲线的叠加得到的，归一化的衰减常数为 0.003567，对应的是在 100% 的呈现时间跨度下，回忆率为 70%（即图右边缘的 R=70%）。图中包含了 401,828 个重复案例。单个曲线用黄色数据点表示。累积曲线由蓝色数据点表示，显示所有 400 条曲线的平均召回率。圆圈的大小与数据样本的大小相对应。

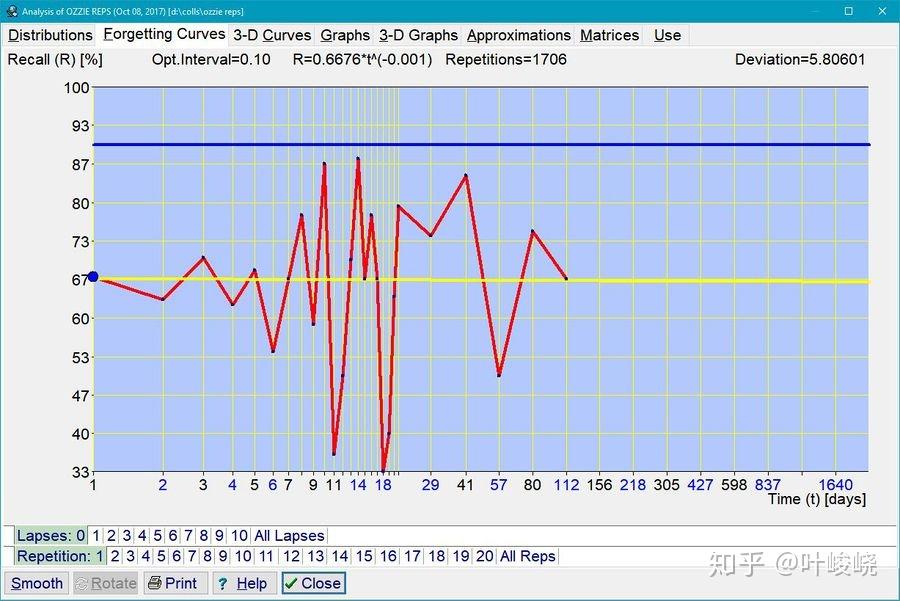
图：一个学龄前儿童的 SuperMemo 集合中的遗忘曲线。没有遗忘表明没有进行有意的陈述性学习。衰减常数几乎为零，这使得最佳间隔没有意义。已记录了 1706 个重复案例。这种平坦的遗忘曲线在旧版本的 SuperMemo 中会被忽视，因为以成人为中心的假设，即在 Day=0 时，可提取性是 100%。随着时间的推移，这条遗忘曲线会向下倾斜，产生一个典型的成人学习曲线图。这个过程可能需要几年的时间，不应该人为地加速，例如通过强制手段。这条曲线是语义脑的一种假设性表达方式。

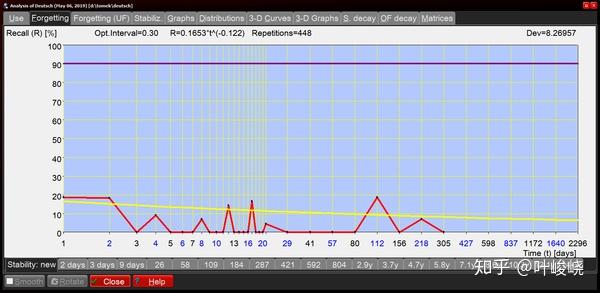
图：优秀的教育者都知道，你不能从外在激励孩子。缺乏内在动机，缺乏记忆技巧，所以 SuperMemo 不适合孩子。在所介绍的案例中，一条遗忘曲线显示，一个 7 岁的孩子在被胁迫学习外语词汇的过程中，表现出灾难性的糟糕。这是一个典型的无语义学习^[5]的案例。这条曲线与孩子的智商没有关系。在这个年龄段，只要使用 SuperMemo 是完全自愿的，有些孩子可能已经表现出一些成功的经验。

原文：Forgetting curve - supermemo.guru

← 返回目录