神经网络:方兴未艾
20 世纪 80 年代中期,我读到迈克尔-阿比伯的《大脑、机器和数学》。这本书巩固了我认为大脑是高效计算机器的观点。
只要对大脑工作机制感兴趣,那么神经网络天然是令人着迷的,而几乎所有人都是如此。在学习计算机科学时(1985-1990年),我对大脑和神经网络有了新的、计算性的看法。神经网络有自行构建模型这个非同寻常的能力,人们很自然地就想到用它来研究记忆数据,来回答记忆如何工作的问题。然而,神经网络有一个重大缺点,就是神经网络不揭露其内部机制。这有点像大脑本身的问题,大脑可以做各种神奇的事情,但却很难说出大脑内部如何运转。编写神经网络软件是很有趣的,我在 1989 年就稍有尝试。但将神经网络应用起来就没那么有意思了。
SuperMemo 的代数方法胜过了神经网络,原因有二:(1)我想回答的记忆方面的问题似乎总是太简单,似乎不用涉及到神经网络,(2)网络需要数据,这些数据从用户学习中产生,而用户学习需要算法,这个算法需要回答记忆的简单问题。在这场先有鸡还是先有蛋的竞赛中,比起利用现有数据和神经网络在那抓耳挠腮,我的大脑还是领先一步。
代数方法的优越性,更体现在求解最优间隔时,只需画出遗忘曲线,使用回归方法,找出回忆率低于 90% 的点即可。这在我的 1985 年的实验[1]中更为极端,我的「遗忘曲线」只由 5 个点组成。我还能选一个我最喜欢的。这简直是学龄前习题。不需要高射炮打蚊子。
1990 年,研究间歇学习模型[2],是我最有可能采用神经网络的时刻。1990 年 7 月 6 日,在与 Murakowski 进行了长达 7 小时的讨论后,我们得出结论,神经网络可以回答一些问题。然而,我的电脑已经在用代数爬山算法疯狂计算数据了。从本质上讲,爬山算法类似于神经网络中的特征提取。一旦我算出了答案,我采用神经网络的动力就消失了。我不需要更好的计算办法。我需要的是更好的数据。
尽管如此,在 1990 年代中期,有越来越多人提问, SuperMemo 算法是否足够有适应性,以及是否有可能在算法中应用神经网络。这些问题的提出者大多不是很了解 SuperMemo 工作效果还不错,能让我们满意。SM-2[3] 这一最早的算法甚至沿用到了今天,其用户大概已达到百万量级。记忆的不满往往源自不合理的期望,这种期望要归咎于学校课程安排。闷闷不乐的情绪,则是因为不善于构建知识来健康地学习[4]的冲动诱发的,而这样的冲动也是从学校中带出来的恶习。SuperMemo 算法无法疗愈对学习的不满。这些算法一贯表现良好,在过去的三十年中给人们带来进步,这是可以量化测量的。对很多用户来说,神经网络就像万能药,有改良一切的本领。
采用神经网络的要求
在 20 世纪 90 年代,发给 SuperMemo World 的邮件经常暗示道,神经网络方法会更优越。即使 SuperMemo 已经推广了十年,学生们还是会写出一系列错误的断言:
SuperMemo 没有考虑到用户能力与需求的不同。相反,SuperMemo 假设每个学习者都是「坏的学习者」。因此每个学习者都会有相同的重复时间间隔。其底层算法是硬性规定的,因此如果你学习方式不同,或者更善于学习,SuperMemo 算法效率不会太高。[...]神经网络能考虑到学习者类型差异很大,不同类型需要不同的最优重复间隔。在复习新单词时,学习者不断「告诉」程序他们做得多好/多坏,他们的学习者类型也水落石出了。有了这种反馈之后,程序能够在必要时适应学习者类型,并优化内在重复间隔。
这些话表明对他 SuperMemo 缺乏了解。SuperMemo 并没有使用什么 「坏学生模型」,只是在还没收集学生记忆数据时,先使用较短的间隔。选择较短间隔的依据是这样能更快收敛到最优解。换句话说,SuperMemo 能够适应学生个体的需要,而「低于平均水平学生的模型」可能指还没收集数据的起始点。神经网络在训练之前也需要选取某个模型,保证时间安排不是完全无规可循的。
在 SuperMemo 中,平均学生模型只是初始条件,之后还会继续计算学生的真实记忆模型。
在有限维的轨迹优化中,有了不错的初始状态猜测,收敛速度就能很快。不过在 SuperMemo 中不是这样,因为最优间隔函数只有简简单单 3 个维度。在一般情况下,对解的搜索可能会失败,而优化也不会成功。与旧版 SuperMemo 中用于研究目的的单价矩阵不同,神经网络算法如果没有经过预训练,结果会是一团乱麻。这就是为什么先前的学习数据被用来更新 SuperMemo 中使用的平均或低于平均的学生模型,以达到最大的收敛速度。
请注意,在 SM-17 算法中,这个平均学生模型更加不重要,因为 SM-17 算法对学习过程中多个参数和函数使用了最佳拟合(比如条目难度,稳定性增长函数)。因此 SuperMemo 总能充分利用现有数据,给出最好结果(使用我们目前最先进的记忆模型知识)。
一个多世纪以来,遗忘曲线的大致形状已经为人所知(见:艾宾浩斯遗忘曲线的错误[5])。SuperMemo 收集了关于不同难度和不同记忆稳定性的条目的遗忘曲线形状的精确数据。从遗忘曲线中,SuperMemo 很容易得出最优间隔。数据只来自一个学生,每一次重复都有助于提高计算精度。换句话说,随着你每一分钟使用 SuperMemo,程序都会越来越了解你。不仅如此,在一两个月后,它就足够了解你了。你永远不需要担心算法的效率问题。
神经网络周围笼罩着神秘的光环。神经网络能够揭示所研究现象的隐藏属性。我们很容易忘记,如果输入了错误的信息,或者缺少一些重要信息,神经网络很容易失败。这就是唯一一例有效应用于间隔重复的神经网络的问题:David Calinski 的 MemAid。
MemAid 的神经网络设计,错在了使用间隔和重复次数作为输入来表示记忆的状态,而这两个变量与稳定性:可提取性不对应。稳定性和可提取性已经证明是描述长期记忆痕迹状态的必要条件[6]。换句话说,MemAid 中的神经网络并没有得到计算最优间隔所需的所有信息。更好的设计会是对完整的重复历史进行编码,例如,使用稳定性和可提取性变量。需要完整的重复历史来说明大量呈现的间隔效应,或在延迟重复中对通过成绩的稳定性的显著提升。然而,Calinski 的设计也能满足在「最优」间隔中学习的基本要求,而很少偏离间隔重复的规则(与算法 SM-2 差不多好)。
SuperMemo 是否缺乏灵活性?
认为 SuperMemo 是有偏见的而神经网络不偏不倚,此言差矣。没有什么能阻止 SuperMemo 中的优化矩阵偏离记忆模型,并产生意想不到的结果。诚然,多年来,随着对记忆工作机制的了解越来越充分,SuperMemo 算法又增添了更多限制,以及定制的小算法。不过这些都不是胡乱猜测的结果。SuperMemo 算法中「偏见」的进步只是反映了前些年的发现。这些发现同样会影响任何神经网络实现,以最大化其表现。
认为 SuperMemo 中优化矩阵的原始预设值是偏见的说法也不对。这些预设值相当于神经网络中的预训练。缺乏预训练的神经网络地收敛到最佳模型也会比较慢。这就是为什么 SuperMemo 是经过普通学生模型「预训练」的。
间隔增长率由最优间隔矩阵决定,而且绝不是恒定的。此外,最优间隔矩阵在时间上的变化取决于用户的表现。只有在使用数月或数年后,算法才感觉像固定下来,稳定不变(算法变化的速度与可用的学习数据量成反比)。算法最终的收敛,反映了人类记忆系统的不变性。使用代数法还是神经网络法来处理优化问题并不重要。最终一个间隔重复函数会现身,反映用户记忆的真实性质。有鉴于此,算法收敛速度应该算作是算法质量的指标。换句话说,间隔函数「固定」下来的速度越快越好。
最后,还有一个领域,神经网络必须使用现有的记忆模型知识(即携带一些偏见),否则就会失去效率。实验性的神经网络 SuperMemo、MemAid 以及 FullRecall 都表现出了一个固有的弱点。当间隔产生预期的效果(如测量的遗忘指数的特定水平)时,网络就会达到稳定。每次网络偏离最优模型时,都会根据重复过程中得到的评分,对最优间隔的数值进行启发式猜测(例如,评分=5 对应于 SuperMemo NN 中最优间隔的 130% 或 MemAid 中的 120%)。另一方面,代数式 SuperMemo 可以计算出一个难度估计,使用准确的保留率测量,并产生一个准确的稳定性增长矩阵的调整值。换句话说,它不会猜测最优间隔。它为那个特定的重复计算出它的精确值。对记忆矩阵的调整是加权的,并产生一个稳定的非振荡收敛。换句话说,正是这种记忆模型使得消除猜测因素成为可能。就这一点而言,代数式 SuperMemo 比神经网络 SuperMemo 的偏见要小。
微调间隔重复算法是徒劳无功的
SM-17 算法是重大进步,然而,许多用户不会注意到这种改进,而坚持使用旧算法。这个认知问题导致了"SM3+ 迷思",我在这篇文章中试图破除这个迷思。同时,新算法对于研究进展是价值连城的。换句话说,实际需求和理论需求之间不不协调。 我在1994 年接受过《Enter》杂志采访,其中所言至今仍然适用:
我们已经看到,进化论代表了 SuperMemo,心理学领域的发现与该方法相吻合,分子生物学的事实和来自沃兹尼亚克模型的结论似乎相辅相成。现在是时候看看所描述的机制是如何在程序中发挥作用的了。在重复的过程中,SuperMemo 为学习者绘制了遗忘曲线,并在保留率(即记忆知识的比例)下降到先前定义的水平时,安排重复。换句话说,SuperMemo 检查你一周后的记忆程度,如果你的记忆低于预期,它会要求你在不到一周的时间内进行重复。否则,它就会在更长的时间后检查你的记忆,并相应增加间隔时间。这个简单的画面有一点小问题,那就是不同难度的项目必须以不同的时间间隔进行重复,而且随着学习过程的进行,时间间隔也会增加。此外,对于一个普通人来说,最优的重复间隔必须是已知的,而且必须在程序能够收集真正的学生的数据之前使用这些间隔。显然,必须有整个数学仪器的参与,以使整个机器运转起来。总而言之,沃兹尼亚克说,在他的一生中,至少有 30 天他有过这样的印象:SuperMemo 中使用的算法已经得到了显著的升级。每一个案例似乎都是一个重大的突破。整个开发过程只是一长串的试验和错误,测试,改进,实施新的想法,等等。不幸的是,那些好日子已经过去了。自 1991 年以来,该算法没有任何突破性的改进。一些安慰可能来自于这样一个事实:从那时起,软件开始快速发展,为用户提供了新的选择和解决方案。那么,SuperMemo 是否还能更好、更快、更有效?沃兹尼亚克是悲观的。任何对算法的进一步微调,应用人工智能或神经网络都会被淹没在干扰的噪音中。毕竟,我们不是在与世隔绝的情况下学习。当程序将下一次重复安排在 365 天后,而事实却在更早的时间被偶然想起,SuperMemo 没有办法知道这个偶然的回忆,它将在之前计划的时间执行重复的工作。这不是最理想的,但它不能通过改进算法来补救。现在改进 SuperMemo 就像在嘈杂的汽车装配车间里对无线电接收器进行微调。SuperMemo World 的人现在不太关注科学。在他们看来,在科学发明之后,SuperMemo 的社会发明时机已经到来。
Dreger 的神经网络项目
1997 年 5 月 20 日,我在前网络 BBS 时代的网友 Bartek Dreger 想出了一个好主意。他还在波兹南科技大学的计算机科学研究所写了关于 SuperMemo 的硕士论文。这将比我自己的晚 8 年,只不过他将使用神经网络来观察它们的表现。尽管他比我年轻近 20 岁,但他的计划是在我在本文其他地方经常提到的那个伟大的 Weglarz 操作研究团队中尝试这个项目。早在 1990 年,Nawrocki 博士就提出了使用神经网络来改进 SuperMemo 的想法。Roman Slowinski 教授的伟大思想将成为监督者。这可能真的有效。
到 1997 年 6 月,我的另一个网友 Piotr Wierzejewski 也加入了这个项目。然后又有三个计算机科学的学生上阵。这是个可爱的团队,由五个年轻人组成,年龄加起来 100 岁。很快,这个项目遇上在线 SuperMemo 的想法,进一步扩展,昵称为:WebSorb(用于从网络(web)吸收(absorb)知识)。我们犯了热情勃发的年轻团队常犯的问题,把计划扩充得太满,最后,只有一小部分目标被实现了。只有在线 SuperMemo 的想法不断发展,虽然非常曲折,中途有一些小项目诞生了又消亡了(例如 e-SuperMemo, Quizer, Super-Memorizer, Memorathoner 等),直到 3GEMs 出现,成为 supermemo.net,最终演变成今天的 supermemo.com。
青年在类似项目中的最大优势是创造力和激情。最大的障碍是学校教育,以及后来的其他义务,包括生孩子。这个神奇的智囊团成了学校这个古老问题的受害者:将一个在激情中诞生的项目转化为一个有截止日期、报告、测试、考试和成绩的学校苦差事。正如这里[3]所解释的那样,SuperMemo也是在那种危险的学校环境中诞生的。成功的关键是为自由而战。枷锁熄灭激情。SuperMemo 的想法之所以在学校教育的压力下幸存下来,是我有推动教育自由的志向。
神经网络式 SuperMemo:为什么记忆模型对 SuperMemo 算法至关重要?
为间隔重复神经网络提出的特征提取是基于这里描述的长期记忆的两个组成部分的存在而得到充分证明的。
记忆双组分模型[6]能够充分表示学习中原子记忆轨迹的状态。有这两个记忆变量,计算最优间隔才有可能,也能将间隔效应纳入考虑。延迟重复的记忆稳定性增长的函数也是已知的。综上所述,只简单的优化算法,SuperMemo 中确定最优重复间隔就是小菜一碟。神经网络则需要对每个项目的全部重复历史进行编码,而最明显的编码选择是记忆稳定性 (S)和记忆可提取性 (R)。换句话说,设计间隔重复算法都依赖相同的基础假设无论算法是代数的还是网络的。毋庸置疑,代数式的解决方案是简单快捷的,收敛速度快,也不需要预训练(最优间隔矩阵或稳定性增长矩阵充分表达了记忆模型)。
基于完整重复历史的神经网络,对于计算记忆稳定性,效果和爬山算法相同。爬山算法对于计算记忆稳定性就是更优越/快速的工具。爬山算法和神经网络有同样的局限,即输出答案的质量受制于输入问题(数据)的质量。
神经网络式 SuperMemo: 设计
我们与 Bartek Dreger 一起设计了一个简单的 ANN 系统来处理间隔重复问题(1997 年 12 月)。请注意,如果没有 Krzysztof Krawiec 博士的专业知识,这个项目是不可能完成的,他对完善设计很有帮助。
存档警告:为什么使用文字档案?
重复间隔问题包括在人类学习的过程中计算最优的重复间隔。这些间隔是针对单个信息(后来被称为项目)和给定的个人而计算的。整个输入数据是学生在学习过程中的项目重复中获得的成绩。到目前为止,这个问题通过一系列连续的算法得到了最有效的解决,这些算法在商业上被称为 SuperMemo,由沃兹尼亚克[7]博士在波兰的 SuperMemo World 开发。沃兹尼亚克在开发最新版本的算法(算法 SM-8[8])时使用的记忆模型[9]不能被视为对人类长期记忆的最终代数描述。最值得注意的是,突触模式的复杂性和项目难度之间的关系还不太了解。一旦采用神经网络来提供记忆状态、评分和项目难度之间的充分映射,就可能对这种关系有更多的了解。
若使用目前最先进的解决方案,在实时学习过程中应用神经网络的技术可能性,还取决于对神经网络遇到问题给出可用定义,而定义这些问题时,合理应用当前对学习过程的理解不可或缺。面对数千条目的重复中得到的历史评分输入,神经网络不可能当即生成出解决方案。实时生成解决方案的计算复杂度和空间复杂度,自然会远远超出网络的实时学习和反应能力。
利用 Wozniak 的长期记忆双组分模型,我们推测以下神经网络解决方案可能会加快收敛,提升高重复间隔的准确性。
描述给定记忆痕迹的状态所需的两个记忆变量是记忆的可提取性(R)和稳定性(S)(Wozniak, Gorzelanczyk, Murakowski, 1995。下面的方程式将 R 和 S 联系起来:
(1) R=e-k/S*t
其中:
- k 是常数
- t 是时间
利用公式(1),给定稳定性,可以得出可提取性随时间的变化;与此同时,给定稳定性和遗忘指数,我们也能确定最佳的重复间隔。
描述重复后稳定性变化的函数的确切代数形状尚不清楚。不过有实验数据表明,对于时机适当的重复,稳定性通常会增加 1.3 到 3 倍,其增量取决于条目难度(难度越大,增加越少)。为让神经网络计算稳定性函数,其预训练可以使用最优间隔重复的估计值,这些值来自 SM-8 算法[8] 的优化矩阵的实验数据。
(2) Si+1=fs(R,Si,D,G)
其中:
- Si 是第 i 次重复后的稳定性
- R 是重复前的可提取性
- D 是条目难度
- G 是第 i 次重复的评分
稳定性函数是第一个需要利用神经网络确定的函数。第二个函数则是项目难度函数,其输入参数与稳定性函数输入参数类似:
(3) Di+1=fd(R,S,Di,G)
其中:
- Di 是第 i 次重复后的条目难度近似值
- R 是重复前的可提取性
- S 是第 i 次重复后的稳定性
- G 是第 i 次重复的评分
因此,一个有四个输入(D、R、S 和 G)和两个输出(S 和 D)的神经网络可以用来封装计算重复间隔所需的全部知识(见:重复间隔神经网络的实现)。
为了验证上述方法的可行性,我们将采取以下方法:
- 神经网络的预训练将根据从算法 SM-8[8] 中使用的函数得出的近似 S 和 D 函数以及收集的实验数据进行。
- 这样一个预训练的网络将被实现为一个 SuperMemo Plug-In DLL,它将取代 SuperMemo 8 for Windows 所使用的标准 sm8opt.dll。在神经网络 DLL 的 alpha 测试中,网络的教学将在一个真正的学习过程中继续进行。一个专门为实验目的而设计的程序将被用来提供累积的结果和一个结果的神经网络。该程序将使用在alpha测试中使用的神经网络来训练将参加 beta 测试的网络。alpha 测试网络将被送入一个输入参数矩阵,其输出将被用作结果网络的训练数据。
- 在最后一步,神经网络的测试将通过互联网直接从 SuperMemo 网站向所有志愿者开放。志愿者只被要求将他们的结果网络提交给实验的最后阶段,在这个阶段,最终的网络将被开发。同样,测试版网络将全部用于训练结果网络。神经网络式 SuperMemo 的未来用户(如果该项目出现成功)将获得一个对人类记忆有相当了解的网络,并能够进一步完善其对学习过程中特定学生的日常活动和特定学习材料的干扰的反应。
所有间隔算法都有一个主要问题,就是是比较最优间隔函数的输出与实际应用特定重复间隔的结果之间,存在一定延迟。在每次重复时,必须记住前一次重复的网络状态,以便生成网络的新状态。在实践中,这相当于在重复之间存储了大量的网络状态。
幸运的是,沃兹尼亚克模型意味着 S 函数和 D 函数与时间无关(有趣的是,它们也可能与用户无关!);因此,可以采取以下方法来简化程序:
| 时间时刻 | T1 | T2 | T3 |
|---|---|---|---|
| 决策 | I1 N1O1=N1(I1) | I2 N2O2=N2(I2) | I3 N3O3=N3(I3) |
| 上一次决策的结果 | O*1 E1=O*1-O1 | O*2 E2=O*2-O2 | |
| 教学评估 | O'1=N2(I1) E'1=O*1-O'1 | O'2=N3(I2) E'2=O*2-O'2 |
其中:
- Ei 是一个与 Oi 的误差约束(见记忆稳定性的误差修正和项目难度的误差修正)
- E'i 是一个与 O'i 的误差约束
- Ii 是 Ti 处的输入数据
- Ni 是 Ti 处的网络状态
- Oi 是 Ni 在给定 Ii 后的输出决策,即在 Ti 进行第 i 次重复后的决策
- O*i 是一个最优输出决策,应该在 Ti 而不是 Oi 处获得;它可以从评分和 Oi 中计算出来(评分表明 Oi 应该如何改变以获得更好的近似值)
- O'i 是 Ni+1 在给定 Ii 后的输出决策,即在 Ti+1 进行第 i 次重复后的决策
- Ti 是某一项目第 i 次重复的时间
上述方法只需要在 Ti-1 和 Ti 发生的重复之间为每个项目存储 Ii-1,大大节省了学习过程中存储的数据量(E'i 和 Ei 一样对训练有价值)。这样,所提出的解决方案在空间复杂度上与算法 SM-8[8] 相当!在整个过程中,只需要记住神经网络的一个(当前)状态。
这些是目前讨论的项目的实现假设:
- 神经网络:单向,分层,有弹性的反向传播;一个有四个神经元的输入层,一个有两个神经元的输出层,以及两个隐藏层(每层 15 个神经元)。
- 项目难度解释:与算法 SM-8 中相同,即由 A-系数定义
- 对每个条目存储以下内容:最后一次重复日期,稳定性(最后一次重复时的),可提取性(最后一次重复时的),项目难度,最后评分
- 默认遗忘指数: 10%
- 神经网络 DLL 输入(在每次重复时):项目编号和当前评分
- 网络 DLL 输出(在每次重复时):下次重复日期
- 神经网络 DLL 实现语言:C++
- 神经网络 DLL 的 shell, SuperMemo 98 for Windows(与 32 位 SM8OPT.DLL shell 相同)
神经网络式 SuperMemo: 实现
该网络实际上已经得到了间隔重复算法的支持。它的唯一作用是随着时间的推移对性能进行微调。这正是所有 SuperMemo 算法如在算法 SM-5[10] 中所做的那样。在这个意义上,这个设计并没有要求网络进行发现。它要求在发现的基础上进行改进。该模型是在设计中加入的。
存档警告:为什么使用文字档案?
基本假设
记忆的状态将只用两个变量即可描述:可提取性(R)和稳定性(S)(Wozniak, Gorzelanczyk, Murakowski, 1995。下面的方程将 R 和 S 联系起来:
(1) R=e-k/S*t
其中:
- k 是常数
- t 是时间
为简单起见,我们将设定 k=1 来统一定义稳定性。
输入和输出
以下函数将由网络求解:
(2) Si+1=fs(R, Si, D, G)
(3) Di+1=fd(R, S, Di, G)
输入给定的 R、S、D 和 G,神经网络应该输出稳定性(S)和条目难度(D):
(4) (Ri, Si, Di, Gi) => (Di+1,Si+1)
其中:
- Ri 是第 i 次重复前的可提取性
- Si 是第 i 次重复前的稳定性
- Si+1 是第 i 次重复后的稳定性
- Di 是第 i 次重复前的条目难度
- Di+1 是第 i 次重复后的条目难度
- Gi 是第 i 次复习时的评分
针对难度 D 的错误修正
目标难度定义为 SM-8 算法中,第二个间隔和第一个间隔的比率。;神经网络插件 (NN.DLL)将记录对所有条目记录目标难度,并将其用于训练网络:
(5) Do=I2/I1
其中:
- Do 是用于误差修正的指导性难度(Do 越高,难度越小)
- I1 是为有关条目计算的第一个最优间隔(对所有条目都一样)
- I2 是为该条目计算的第二个最优间隔
重要!最优间隔 I1 和 I2 不是网络在验证前提出的间隔,而是在提出的间隔已经执行和验证后用于误差修正的间隔(见稳定性 S 的误差修正)!
难度的初始值将设为 3.5,即 D1=3.5。这只是为了与算法 SM-8 相似。由于初始难度未知,所以不能用初始难度求解第一个间隔。第一次评分之后,由于第二个最优间隔也是未知,所以仍然无法进行误差修正。一旦得知第二个最优间隔,Do 就可以用来对输出的 D 进行误差修正。
为了避免神经网络的收敛问题,下列公式可用于求出正确的 D 输出:
(6) Dopt=0.9*Di+0.1*Do
其中:
- Dopt 是在第 i 次重复后用于误差修正的难度
- Di 是第 i 次重复前的难度
- Do 是指导性难度,由公式 (5) 可得
公式 (6) 中的收敛系数 0.9 是随意取的,可能会根据神经网络表现而改变。
稳定性 S 的误差修正
下列公式是将公式 (1) 中遗忘指数取 10%,令 k=1 而得出的。这个公式方便转换稳定性和最优间隔:I=-ln(0.9)*S
在最好情况下,神经网络应该每次重复都生成一次所需遗忘指数。只要已知稳定性 S (见公式 (1)),变化遗忘指数也很容易使用。为了简单起见,进一步分析中遗忘指数取 10%。
为了加速收敛,神经网络将测量 25 类重复的遗忘指数。这 25 类重复的划分是根据 (1) 五个难度类别:1-1.5、1.5-2.5、2.5-3.5、3.5-5 和 5 以上,和 (2) 五种间隔时长类别:1-5、5-20、20-100、100-500 和 500 天以上。我们将这些类别的遗忘指数测量值表示为 FI(Dm,In)。此外,我们还测算总体遗忘指数 FItot,并将其用于稳定性的误差修正。
最终目标是在所有类别的遗忘指数达到 10% 。下列公式将用于误差修正以保证结果的稳定性:
(7) FIopt(m,n)=(10*FItot+Cases(m,n)*FI(m,n)) /(10+Cases(m,n))
其中:
- FIopt(m,n) 是属于 (m,n) 类的重复之后,用于误差修正的遗忘指数
- FItot 是总体遗忘指数,以重复次数衡量
- Cases(m,n) 是用于衡量类别 (m,n) 中遗忘指数,以重复次数计量
公式 (7) 中的公式应该是在单独类别的案例数量增加时,将纠错的权重从总体遗忘指数转移到特定类别记录的遗忘指数上。很明显,对于 Cases(m,n)=0,我们有 FIopt(m,n)=FItot。对于 Cases(m,n)=10,整体和类别 FI 的权重平衡,对于大量的案例,FIopt(m,n) 接近 FI(m,n)。
下表说明了 FIopt(m,n)、评分和使用的间隔校正之间的假定关系:
| 评分 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| FIopt(m,n)>10% | 40% | 60% | 80% | 无修正 | 无修正 | 无修正 |
| FIopt(m,n)=10% | 无修正 | 无修正 | 无修正 | 无修正 | 无修正 | 无修正 |
| FIopt(m,n)<10% | 无修正 | 无修正 | 无修正 | 110% | 120% | 130% |
在 SuperMemo 中,小于 3 的评分代表遗忘,而评分等于 3 或大于 3 则代表充分回忆。这就是为什么在 FI 达标的情况下,不对合格的平分进行修正,而在 FI 大于要求的情况下,不对不合格的评分进行修正。在应用间隔为 10 天的情况下,对过度遗忘率和评分 = 2 的示例性修正是 80%。因此,网络将被指示假定间隔 = 8 为正确。然后,正确的稳定性将从 S=-8/ln(0.9) 中得出,并用于纠错。间隔修正的值是任意的,但不应该破坏网络的收敛性。在不可能出现稳定性问题的情况下,可以减少修正值(注意,学习过程中的环境噪声将大大超过无效选择修正因子的影响!)。类似的修正曾经被应用于连续的 SuperMemo 算法中,结果令人鼓舞。
边界条件
为了加速收敛,将对神经网络施加以下额外约束:
- 连续两次重复的间隔增长倍数必须至少是 1.1(因此,难度不能低于 1.1)
- 第一次重复的间隔增长倍数不能超过 8,以后的重复中不能超过 4
- 第一个间隔必须在 1 到 40 天之间
- 难度度量不能超过 8
这些条件不会使网络更有偏见,因为在过去十年使用 SuperMemo 及其实施的实践中,这些条件已被证明是真实且完全合理的。
预训练
在预训练阶段,将使用公式(2)和(3)的如下形式:
(8) Di+1:=Di+(0.1-(5-G)*(0.08+(5-G)*0.02))
(9) Si+1:=Si*Di*(0.5+1/i)
其中 D1=3.5, S1=-3/ln(0.9)。
公式 (8) 是由 SM-2 算法推导出来的(见 E-系数公式)。公式(9)是由算法 SM-8 中的矩阵 OF 大致导出的。D1=3.5 对应于算法 SM-8 中的相同设置。S1=-3/ln(0.9) 对应于第一个间隔 3 天和遗忘指数 10%。3 天的数值接近于各种学生和学习材料难度的平均值。
预训练也将使用上一段中提到的边界条件。
神经网络存在多种问题,实现、bug、收敛、干扰等等。研究神经网络的唯一有效方法是将其应用到真正的 SuperMemo 中,看看神经网络如何使用真实数据工作的。我有个想法是把算法写入一个 DLL 里。我们可以在同一程序 shell 中研究算法的变体。我们对 SM-2 算法、SM-8 算法 都有类似尝试,现在对神经网络也可如法炮制。不幸的是,这个 DLL 想法的实现还是为时过早。参加项目的孩子们热情如炽,而他们一毕业便散做满天星,在其他地方找到工作,娶妻结婚,而我从来没有机会在我自己的学习中尝试这个插件,在我最喜欢的 shell 中,当时是 SuperMemo 9(又名 SuperMemo 98)。
神经网络 SuperMemo 是学生项目,其唯一目的是验证神经网络应用于间隔重复的可行性。毋庸置疑,神经网络是可行的。此外,所有可以想象到的有效优化工具,只要充分打磨,必然会产生与 SuperMemo 目前所实现的类似结果。换句话说,只要学习程序能够快速收敛到最优模型,并产生期待中的知识保留率,用于完成目标的优化工具是次要的。
考虑到这个项目早期阶段的问题数量,我怀疑成功的插件会改变我对神经网络的想法。我是程序员,喜好摆弄东西,我喜欢看我创造的东西。神经网络对我来说显得太黑箱了。至于这个团队,他们今天的事业都很成功。这些孩子们后来还为其他一些 SuperMemo 工作做出了贡献。青年有蓬勃创意,青年是难解谜团,能启动这个项目,我不胜欢欣。
David Calinski 和 FullRecall
大卫-卡林斯基(生于 1981 年)是 20 世纪 90 年代早期年轻的 SuperMemo 爱好者之一。他对加速学习、心理学、精神病学等方面表现出丰富的兴趣。
我很快就认识到了他的才能,并希望在一些 SuperMemo 项目中招募他,包括 SuperMemo for Linux,然而,许多天才喜欢独行。在某些时候,他从 SuperMemo 转向了他自己的应用程序(FullRecall,见后文),从那时起,他就不会放弃他的项目。
我们关于神经网络的讨论始于 2001 年。David 是 SuperMemo 的粉丝,然而,他也承认自己从未真正研究过该算法。这导致他写下如下批评:
我不知道 SM 算法的具体细节(我从来没有对它感兴趣过),但重要的是想法纲领。SM 的算法输入一些数据(如重复次数、项目难度、当前评分等),并返回计算出的下一个最优间隔。这个算法即使是 「聪明的」,也就是能以某种方式纠正自己,也仍然是愚蠢的——其修正能力不超过其设计所赋予的。
他是对的,算法 SM-17 与长期记忆的双组分模型有内在的联系,然而,这两者是相得益彰的。这种结合只能由反面证据来打破,而反面证据到目前整整三十年还没有出现。
大卫的立场是完全有道理的。这都是关于建模和先验知识。对大卫来说,SM-8 算法很复杂。神经网络似乎是消除复杂度的简单方式。对我来说,我自己的算法就像乘法表一样简单。这种建模差异往往会导致认知上的分歧,这是件好事。如果没有这些差异,我们今天对间隔重复中的神经网络的了解就会少得多!
在 2004 年,我写信给大卫:「对 SuperMemo 中使用的算法的进一步改进不可能导致学习的进一步加速。然而,在处理异常情况方面仍有改进的余地,如大幅延迟的重复、短时间集中展示、处理内容改变的项目、处理项目之间的语义联系等等。有趣的是,该算法的最大进步可能来自于对人类长期记忆模型的更好定义。特别是,描述不同可提取性水平的记忆稳定性变化的功能正在被更好地理解。这可以极大地简化算法。更简单的模型需要更少的变量,这就简化了优化工作。基于记忆痕迹的稳定性和可提取性的算法也可以更好地处理低可提取性的项目。然而,由于在学习过程中,异常的项目案例只占少数,而且测试一个新的算法需要几年的时间,目前还不清楚是否会进行这样的实施。」
大卫开发了他自己的神经网络 MemAid。后来他将其转化为商业产品。从免费到商业的转变是艰难的,原因显而易见,因为用户往往更喜欢价格下降。尽管经历了种种波折,大卫还是坚持了下来,他的 DIY 修理工以及对科学和编程的热情总是让他占了上风。像 Anki 一样,他试图保持他程序的跨平台性,这对简单性有一些限制和要求。用他的话说:「我喜欢速度,喜欢没有边界,喜欢不只依赖一种方案、系统、电脑等。」
今天 FullRecall 是免费的。见 changelong。
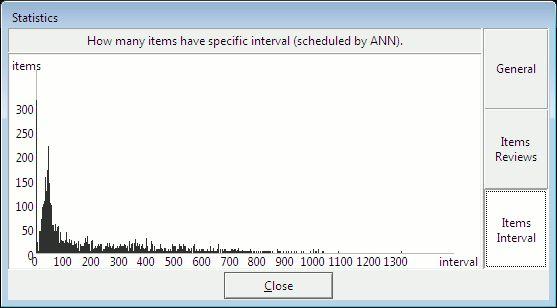
图:FullRecall 中的间隔分布。在神经网络的帮助下安排复习。
开源的 MemAid 项目于 2006 年关闭,但 FullRecall 继续进行。另一个受 MemAid 启发的项目也是如此:Mnemosyne。然而,Mnemosyne 选择了他们自己版本的算法 SM-2。时至今日,Mnemosyne 产生的数据可供间隔重复爱好者或 Mnemosyne 项目的研究人员使用。
与 Calinski 一样,Peter Bienstman 对较新的算法持怀疑态度:「SuperMemo 现在使用 SM-11。然而,我们有点怀疑较新的 SM 算法的巨大复杂性是否提供了统计学上的相关好处。但是,这也是我们希望通过数据收集找出的事实之一。」
「统计学上的相关利益」取决于标准。对于用户来说,实际的算法可能是次要的。对于研究来说,算法 SM-17是一个金矿(和 Mnemosyne 等所有程序能产生的数据一样多)。
为什么 FullRecall 的神经网络是有缺陷的?
两个记忆变量对于表示间隔重复中的原子记忆来说,既是必要的也是充分的。此外,这两个变量还可以用来解释大量呈现中的间隔效应。它们还可以解释这里讨论的高遗忘指数对长期保留的好处。这两个长期记忆的变量,我们称之为:稳定性和可提取性,是表示记忆状态的必要条件。任何想要在间隔和回忆之间的关系中找到模式的神经网络必须在其输入中接收完整的记忆状态,否则它将永远无法计算出最优间隔。这种状态可能有完整的重复历史的形式。它也可以是稳定性:可提取性对(如果它可以被计算出来)。它也可以是重复历史上的任何其他代码,从中可以计算出记忆的状态。
FullRecall 神经网络的设计并不符合这些标准:
- 输入:last_interval_computed_by_ann(根据 ANN 得出的最后一次间隔)[0-2048天](如果不是复习,而是第一次展示,则为零)
- 输入:real_interval_since_last_review [0-2048天] (与上面的注释相同)
- 输入:number_of_repetitions_of_an_item_so_far (目前为止条目的重复次数)[0-128]
- 输入: current_grade(目前评分)[0-5, 5 是最好的]
- ANN 给我们的输出是:new_interval(新间隔)[0-2048]
间隔和重复次数都不能反映记忆的稳定性和可提取性。可能在使用间隔效应的大量内容学习中重复多次,但是记忆稳定性提升却微乎其微。长间隔的次优计划可能导致稳定性和可提取性较低。简而言之,对于相同的间隔,记忆的状态将取决于重复的时间分布。
可以举例说明:在 1000 天内安排 10 次重复,如果安排是 9 天内 9 次重复,其中有 991 天的间隔,那么最终记忆稳定性接近于 0(假设没有其他干扰)。与此同时,如果输入相同,而间隔安排最优,那么可提取性将接近 100%, 而稳定性也极高,因而可以安排接近 1000 天的最优间隔。
只有用户分毫不差地按照最优间隔重复安排复习,神经网络才能有不错的表现。要实现这点,神经网络只有经过预训练才可行,比如使用 SM-2 算法 预训练。此时神经网络会很不稳定,也无法收敛到最优解,因为有很多偏离最优安排的复习,比如神经网络误差导致的复习,这些复习会让神经网络偏离原始状态,而原始状态下神经网络还能根据输入计算记忆情况。
在理想化的情况下,稳定性和可提取性对于单一的单突触关联来说是足够的。在现实生活中,参与联想的语义网络很可能涉及一些这样的理想单元记忆。这就是为什么 SuperMemo 使用绝对条目难度。在 SM-17 算法中,绝对条目难度是由默认的遗忘指数为 10% 时,第一次优化安排的复习的记忆稳定性的最大增幅决定的。FullRecall 网络没有输入项目难度的可靠衡量,因而神经网络低效问题更加严重。
根据用户报告,FullRecall 网络似乎工作得相当好。根据目前的分析,该网络可能采用了精心选择的边界条件,然而,这样就相当于回到了 SuperMemo 旧版本中采用的算法 SM-2。不用说,那个老的 SuperMemo 算法比 SuperMemo 中新的基于矩阵的代数算法更有偏见,可塑性更差。
如果 FullRecall 网络是预先训练好的,例如在算法 SM-2 的帮助下,学生严格地坚持他或她的重复,网络可能工作得很好,因为间隔与记忆的稳定性有很好的关联,特别是如果信息被重复的次数所加强。然而,如果没有适当的边界条件,在渐进阅读中,该网络肯定会失败,因为它可能收到错误的记忆状态信息。根据不同的情况,相同的重复次数:间隔对可能出现在稳定性=0 和最大稳定性对应的终身记忆中。同样,对于网络中的同一输入对,可提取性也可能在 0-1 范围内变化。例如,在考试前频繁地进行子集复习,然后是较长时间的学习中断(例如由溢出引起的),可能对应于非常低的稳定性和可提取性,尽管在同一时期提供与正确执行一系列间隔复习相同的输入(具有高稳定性和高于 0.9 的可提取性)。在渐进阅读中,过载、自动延期、项目提前、筛选集复习和间隔效应对网络来说是不可见的。
假设设计良好,那么 FullRecall 的缺陷只会在间断性学习中显示出来,这可能会触发边界条件。这不应该减损软件本身的价值。它只是要强调,神经网络的设计并不容易,而且可能会变成劣质的。它甚至可能不如旧的、据说可塑性较低的代数算法。
简而言之,FullRecall 网络输入并没有反映出计算最优间隔所需的所有必要信息。特别是,重复次数是衡量记忆稳定性或可提取性的一个非常差的标准。更好的方法是对整个重复历史进行编码,或者使用稳定性和可提取性变量来计算记忆的状态。稳定性和可提取性都必须是可以从网络输入中计算出来的。
SuperMemo 中神经网络的前景
在我们与 Calinski 的讨论中(2001年),我总结了我的保留意见,并发誓要继续走老的「保守」道路。17 年后,我很高兴。在运用神经网络进行间隔重复的领域里,并没有什么进展。可能 SuperMemo 本身也在抑制这一进展。但与此同时,算法SM-17 已经揭示了在间隔重复和理解人类记忆方面继续进步仍是可能的。假以时日,定有进益。
SuperMemo 将沿用其代数算法,理由如下:
- 已知的模型:在我们不知道映射现象的基本模型的情况下,神经网络更有优势。遗忘的模型是众所周知的,这使得计算重复间隔时使用的代数优化方法容易进行微调。众所周知的模型也使得 SuperMemo 能够抵抗不平衡的数据集,这可能困扰着神经网络,特别是在学习的初始阶段。最后但同样重要的是,记忆的双组分模型的有效性已经在许多方面得到了证明,在设计网络时放弃该模型,以阻止偏见的名义,将是浪费。这种方法可能只具有研究价值
- 过拟合:由于数组值的个案加权变化,SuperMemo 中使用的优化数组不会受到「过拟合」的影响。不需要进行预训练,因为事先知道最优间隔的函数的近似形状。不存在数据表示问题,因为所有磕磕碰碰的数据输入都会在时间上被「权衡」出来
- 等价性:从数学上讲,对于连续函数,在具有 n 个参数的映射函数中,n 个输入网络等同于 n 维数组,除了「参数解析问题」。参数解析问题的范围,即参数值范围的有限数量,强烈依赖于函数。对 SuperMemo 所显示的优化数组的短暂窥探表明,「参数解析」远远好于这种特殊类型的函数的实际需要,尤其是考虑到数据中的大量「噪音」。SuperMemo 中使用的爬坡算法让人想起了旨在重新加权网络的算法
- 研究:SuperMemo 中矩阵的使用使我们很容易看到「进行中的记忆」。神经网络就没有那么好观察了。它们不能有效地揭示其结论。你无法看到一条遗忘曲线如何影响最优间隔的函数。这意味着,神经网络的黑箱性质使得它们作为记忆研究工具不那么有趣
- 收敛性:算法的复杂性并不是由记忆模型的复杂性造成的。大部分的复杂性来自于工具的使用,这些工具被认为是为了在不损害其稳定性的情况下加快优化程序的收敛速度。这种微调之所以能够实现,是因为我们对底层记忆模型有很好的了解,以及多年来收集的实际学习数据,这些数据帮助我们精确地确定了模型各个组成部分的最优近似函数
- 遗忘曲线:确定给定遗忘指数的最优间隔的唯一方法是知道给定难度等级和记忆稳定性的(近似)遗忘曲线。如果一个神经网络不试图映射遗忘曲线,它将总是围绕最优间隔的值振荡(好的评分会增加该值,而坏的评分会减少该值)。由于数据噪音的存在,这只是一个理论上的问题。然而,它说明了稳定性-可提取性-困难-时间关系的符号表示的力量,而不是几乎无限多的可能遗忘曲线数据集。如果神经网络不使用遗忘曲线的加权映射,它将永远不会收敛。换句话说,它将一直围绕着最佳模型进行振荡。如果神经网络权衡了状态历史和/或采用了遗忘曲线,它将采取与现在的 SuperMemo 算法相同的方法,而这种方法首先是要被网络所避免的
总之,神经网络可以用来计算间隔,但从计算能力、研究价值、稳定性以及重中之重的收敛速度来看,神经网络似乎不是最好的工具。设计最优神经网络会遇到与设计代数优化程序类似的困难。最后,在「经典」SuperMemo中设置的边界条件也会迟早出现在网络设计中(可以看:神经网络 SuperMemo)。
与其他函数逼近手段一样,工具选择不同,或是对算法稍一微调,收敛速度和映射准确性便有天壤之别。神经网络可用于求算一些所知尚少的附属函数,这些附属函数可用于加快代数算法的收敛速度。例如,时至今日,条目难度估计问题还没有完全破解。我们只是告诉用户要让知识表述简单。任何教育家,只要意识到人类记忆存在限制,都会提出这一建议的。
总目录:0 目录《间隔重复的历史》
Thoughts Memo 汉化组译制
原文:1997: Employing neural networks
参考
1. 1985:SuperMemo 的诞生 ./95111167.html2. 1990:记忆的通用公式 ./429504395.html
3. SuperMemo 1.0: 日志 (1987) ./97887756.html
4. 死记硬背(填鸭式学习) ./360416156.html
5. 艾宾浩斯遗忘曲线的错误 ./156672476.html
6. 1988:记忆的两个组成成分 ./99505568.html
7. 彼得 · 沃兹尼亚克 ./303204832.html
8. 1995:超媒体 SuperMemo ./447640544.html
9. 记忆的神经统计模型 ./277483881.html
10. 1989: SuperMemo 适应用户记忆 ./205600711.html

