[本科毕设] 基于 LSTM 和间隔重复模型的复习算法研究

没想到自己毕业快一年了，我的论文还在 IEEE TKDE 的 Early Access 阶段^[1]。之前说好要将论文内容发在知乎上，但怕中间出什么幺蛾子，我还是打算等到正式刊出后再发。不过那篇顶刊论文其实是我毕业论文的浓缩版，所以我这里直接公开我的本科毕设，大家就能了解那篇论文的主要内容了。这篇本科毕设放在学校档案室最终也是发霉，还不如发在知乎上供大家学习参考。

注：这篇论文为了水到 40 页，塞了很多无聊的背景介绍，大家可以直接从第 3 章开始看。论文篇幅较长，请善用知乎自带的目录功能。本论文的 Latex 源码请见：

hithesis/examples/hitbook/chinese at master · L-M-Sherlock/hithesis · GitHub

哈尔滨工业大学深圳校区毕业设计（论文）

题目：基于 LSTM 和间隔重复模型的复习算法研究

作者：叶峻峣

导师：苏敬勇

答辩日期：2022 年 6 月 2 日

摘要

间隔重复是一种记忆方法，学习者按照给定的复习周期重复记忆，可以有效地形成长期记忆。为了提高记忆效率，间隔重复的调度算法需要对学生的长期记忆进行建模，并优化复习的成本。该文提出了一种间隔重复调度算法，包含了长期记忆预测和复习最优规划两个部分。

在长期记忆预测方面，该文分析了现有的记忆模型预测误差较大的原因，认为传统模型缺乏对记忆行为时序特征的挖掘和利用。通过使用长短时记忆循环神经网络（LSTM）对记忆行为序列进行学习，结合半衰期回归（half-life regression, HLR）模型，该文提出了 LSTM-HLR 模型，相对目前最先进的模型，降低了 80% 的预测误差。

在复习最优规划部分，该文对最优化的目标进行了探讨，认为最小化学习者的复习成本是一个有实际意义的指标。通过使用 LSTM-HLR 预测长期记忆的动态变化，该部分构建了一个马尔科夫决策过程，并将最优化问题转化为随机最短路径问题。基于随机动态规划方法，计算得到最优的复习策略 SSP-MMC。与最先进的方法相比，SSP-MMC 节省了 15.12% 的复习时间。

关键词：间隔重复；长期记忆；长短时记忆网络；随机最优控制

第 1 章绪论

1.1 研究背景与意义

在学习中，记忆发挥着重要的作用。大量基本认知任务依赖于记忆，例如，学生通过阅读材料来学习时，需要从记忆中检索大量背景知识，才能理解材料内容[1]。可以说，记忆是学习中重要的一环。Ebbinghaus 在 1885 年通过定量实验分析，发现了遗忘曲线，其刻画了在没有复习的情况下，记忆随着时间衰退的现象[2]。为了克服遗忘，传统的记忆方式是集中重复，即在短时间内大量重复一段材料。有神经科学实验表明，集中重复是一种低效的记忆方式，因为集中重复不能有效地增强神经元连接强度的长期增益效应[3]。与集中重复不同，间隔重复是一种将复习分散到多天内进行的记忆方法。有大量记忆任务实验[4]和生物学实验[5]表明，间隔重复能有效地增强长期记忆，在效果上优于集中重复。

近年来，有大量研究表明，在间隔重复中，间隔的长短会影响记忆的效果[6-7]。怎样的间隔安排是最好的，一直是该领域的热点问题。随着教育技术不断发展，间隔重复的应用范围也越来越广，特别是在在线学习平台上为学习者安排复习任务。许多研究表明，除了语言学习[8]领域外，间隔重复在医学[9]、统计学[10]、历史[11]等领域也同样有效。

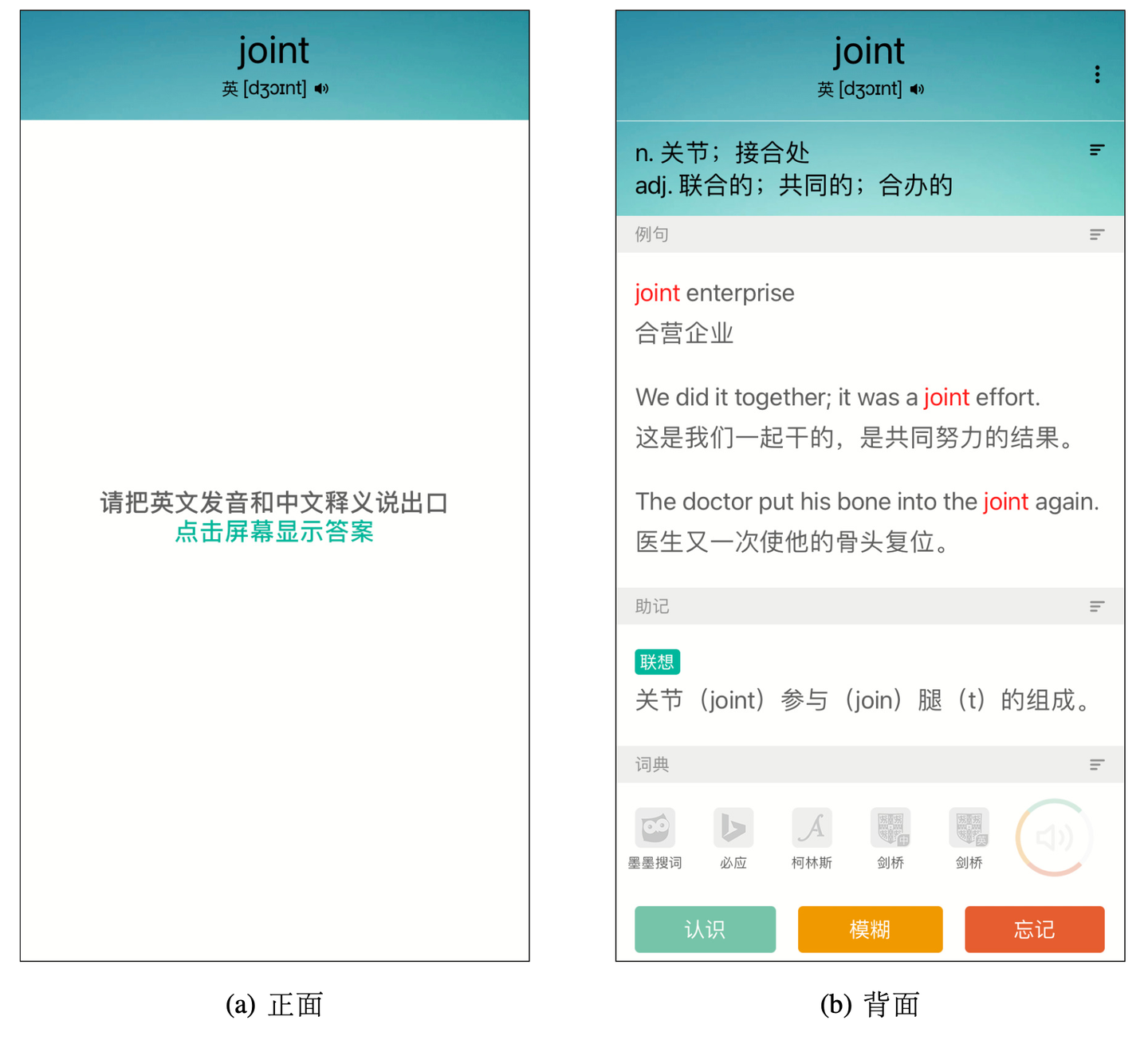
在大多数间隔重复的实践中，材料是以抽认卡的形式呈现的，如图 1-1 所示，并使用简单的调度表确定每张抽认卡的复习时间。关于如何设计一个更有效的间隔复习调度算法的问题有着丰富的历史。从 Leitner 盒到第一个间隔重复软件 SuperMemo，他们都是以设计者的经验和个人实验为基础，使用简单的规则启发式算法。许多间隔重复软件（Anki, Mnemosyne 等）仍然使用这些算法。由于硬编码的参数和缺乏理论证明，这些算法不能适应不同的学习者和材料。同时，它们的性能也不能得到保证。

随着在线学习平台的普及，越来越多的学生在网上学习，这使得收集大规模学习数据成为可能。在大数据的基础上，通过数据挖掘和机器学习构建智能间隔重复系统的研究已经兴起。而复习调度算法是智能间隔重复系统的核心之一。在墨墨背单词这个支持学习者记忆词汇的语言学习应用中，一个高效的间隔重复调度算法可以节省数百万学习者的时间，并帮助他们记住更多的单词。

根据定义，间隔重复天然地产生一系列时间序列事件，然而目前对复习调度算法研究普遍基于人工挑选的特征，且缺乏对时序信息的利用。此外，大部分研究往往只专注于间隔重复系统的某一模块，对其余模块进行了简化处理。这使得调度算法往往运行在过度理想化的环境中，无法用于真实的在线学习平台。

1.2 本文的主要工作

本项工作将构建一套完整的间隔重复系统，提高学习者的记忆效率，其包含记忆预测与复习调度两个模块。

复习调度的本质是如何在合适的时机安排复习，以最大化学习者的长期记忆。这要求系统应能预测学习者的长期记忆状态。有多项工作[12-13]使用回忆概率和记忆半衰期来描述长期记忆，将长期记忆预测建模为一个回归问题。本项工作构建了 LSTM-HLR 模型，利用学习者在间隔重复过程中产生的时序数据训练，对学习者的记忆半衰期和回忆概率进行预测。而在复习调度算法的相关研究中，学习者被假定在有限的时间内记忆材料，

并期望在截止期限到来时能最大化所记忆的材料数量[14]。考虑到记忆和遗忘存在随机性，可作为随机最优控制问题来研究。

在本文中，本文根据收集到的数以百万计的记忆数据，建立了用于模拟学习者长期记忆的 LSTM-HLR 模型。本文设定了一个具有实际意义的明确的优化目标：使学习者形成长期记忆的记忆成本最小化。为了实现这一目标，本文提出了一种新颖的间隔重复调度算法，即 SSP-MMC（Stochastic-Shortest-Path-Minimize-Memorization-Cost）。

目前拥有完整时序信息的大规模数据集是清远墨墨教育科技有限公司在墨墨背单词 APP 上收集的学习者记忆行为数据，考虑到数据限制和项目时间限制，本文没有在其他学习领域测试本文的复习调度算法。

本文的工作为间隔重复调度算法提供了一个更接近实际环境的长期记忆模型，并通过现实世界的数据进行了测试。本文找到了一个可能的间隔重复调度的优化问题和相应的最优化方法。综上所述，本文的主要贡献是：

建立并公开发布本文的间隔重复日志数据集，这是第一个包含时间序列信息的数据集。
据本文所知，这是第一个采用时间序列特征来模拟长期记忆的工作。
在预测长期记忆和优化复习调度方面，LSTM-HLR 和 SSP-MMC 优于最先进的基线。

1.3 本文的结构安排

第二章（背景）首先，为了更好地理解这项工作所需的相关理论概念，一一介绍了相关领域的历史发展。然后列出了在这个问题领域已经完成的或与本文试图解决的问题相关的一些工作。

第三章（方法）介绍了系统的组成模块和模块设计，包括记忆预测和复习规划两个部分，和将两者结合起来的间隔重复系统。

第四章（实验）详细介绍了数据集、实验设置，包括参数设置和模型结构。

第五章（分析与讨论）给出了实验结果和分析，并讨论了这项工作可以扩展的方式。它还从可持续性和伦理道德的角度列出了这项工作可能产生的影响。

最后，（结论）对本文的研究结果进行了总结。

第 2 章间隔重复调度算法相关工作

本工作主要涉及对记忆模型、调度算法的设计，应用了循环神经网络和最优控制相关的工具。因此，本章将先介绍记忆模型和调度算法的相关工作，然后补充循环神经网络和最优控制的基本原理。

2.1 长期记忆预测模型

2.1.1 Ebbinghaus

Ebbinghaus 关于遗忘曲线的经典研究表明[2]，如果在首次记忆材料后不进行复习，材料就会逐渐被忘记。遗忘的程度与不进行复习的时间存在函数关系：

$\begin{equation} b = \frac{k}{(\log t)^c + k} \end{equation}$ (2-1)

式中

$b$ ———再次记忆时节省的时间与第一次记忆所花时间之比，相当于第二次记忆时还保留多少第一次记忆的内容；

$t$ ———第二次记忆与第一次记忆之间间隔的时间；

$c$ 和 $k$ 这两个参数并未明确定义，但观察其二阶导数可知， $k$ 越大，遗忘的速度越慢， $c$ 越大，遗忘的速度越快。Ebbinghaus 在它的研究中尚未给出不同的记忆过程对这些参数的影响。

2.1.2 Wickelgren 广义幂律

Wixted 和 Carpenter[15]指出，回忆的概率随着时间以幂函数衰减:

$m=\lambda(1+\beta t)^{-\varPsi}$ (2-2)

式中

$\lambda$ ———代表初始学习程度的常数；

$\beta$ ———时间比例因子；

$\varPsi$ ———遗忘率；

在这项工作中，Wixted 对比了幂函数和指数函数对艾宾浩斯对遗忘曲线的拟合度，发现幂函数能更好地拟合艾宾浩斯的遗忘数据。在一项使用大数据来预测和改进学习者记忆保留的工作中，研究人员结合广义幂律函数，提出 DASH 模型来估计学习者对材料的遗忘情况，通过材料的难度、学习者的能力和学习历史来估计公式 (2-2) 中的参数大小[16]。

2.1.3 ACT-R 陈述性记忆模块

Pavlikp 和 Anderson[17]使用以下模型来描述遗忘过程

$m_\mathrm{n}(t_\mathrm{1..n}) = \beta + \ln(\sum\limits_{k=1}^n t_\mathrm{k}^{-d_\mathrm{k}})$ (2-3)

式中

$m$ ———记忆的强度；

$d$ ———第 $k$ 次复习时的记忆强度衰减率；

$\beta$ ———材料难度;

$p(m) = \frac{1}{1+e^{\frac{\tau-m}{s}}}$ (2-4)

式中

$\tau$ ———激活阈值参数；

$s$ ———控制激活中噪声的影响，描述了回忆对激活变化的敏感性；

适应性思维特征-理性模型（Adaptive Control of Thought—Rational, ACT-R）[18]是一种认知体系结构，其包含了陈述性记忆模块，假设每次练习会尝试一条幂函数遗忘曲线，多个幂函数近似了间隔重复后的遗忘曲线。

2.1.4 多尺度上下文模型

Pashler 等人[19]通过结合两种心理学模型，得到了以下公式：

$s_{N}(t)=\sum\limits_{i=1}^{N} \gamma_\mathrm{i} \exp \left(-\frac{t}{\tau_\mathrm{i}}\right) x_\mathrm{i}(0)$ (2-5)

式中

$\tau$ ———激活阈值参数；

$s$ ———控制激活中噪声的影响，描述了回忆对激活变化的敏感性;

多尺度语境模型（Multiscale Context Model, MCM）[19]假设每次练习都会产生一条指数函数遗忘曲线，使用多个指数函数叠加来近似遗忘曲线。

2.1.5 半衰期回归模型

Settle 和 Meeder[12]提出了记忆半衰期的概念，并用指数函数来刻画回忆概率与时间的关系：

$p = 2^{-\Delta/h}$ (2-6)

式中

$p$ ———正确回忆一个项目（例如，一个单词）的概率；

$\Delta$ ———上次练习该项目以来的滞后时间；

$h$ ———学习者长期记忆中的半衰期或强度度量；

当 $\Delta = h$ 时，滞后时间等于半衰期， $p=2^{-1}=0.5$ 时，学生处于遗忘的边缘。这项工作假设回忆只能是二进制的，即回忆成功或回忆失败。

半衰期被假设随每次重复曝光呈指数增加。估计的半衰期 $\hat{h}_{\bm\Theta}$ 由下式给出：

$\begin{aligned} \hat{h}_{\bm\Theta}&=2^{\bm\Theta \cdot \bm x}\\ \bm x &= (x_\mathrm{\oplus},x_\mathrm{\ominus}, \bm{lex}) \end{aligned}$ (2-7)

$\bm x$ ———描述学生-项目对的学习历史的特征向量；

$\bm\Theta$ ———对应于 $\bm x$ 中的每个特征变量的权重；

$x_\mathrm{\oplus}$ ———学习对该项目历史回忆正确的次数；

$x_\mathrm{\ominus}$ ———学习对该项目历史回忆错误的次数；

$\bm{lex}$ ———词位向量，代表单词的标签；

由于 HLR 挑选的特征向量只包含统计信息，无法捕捉记忆在时序上的特征。此外，HLR 模型通过机器学习的方式来训练 $\bm\Theta$ 的大小。损失函数为：

$loss=(p-\hat p)^2 + \alpha(h-\hat h)^2 + \lambda||\bm\theta||^2$ (2-8)

式中

$\hat p$ ———回忆概率预测值；

$\hat h$ ———记忆半衰期预测值；

$\lambda$ ———正则化系数；

虽然 HLR 模型考虑了降低记忆半衰期的误差，但仅考虑了绝对误差，而没有考虑绝对百分比误差更接近实际情况。

2.2 间隔重复调度算法

2.2.1 Pimsleur 方法

Pimsleur 提出在外语学习中使用递增间隔进行记忆，并刻画间隔重复下遗忘曲线的变化[20]。Pimsleur 的复习间隔以 5 为底指数增长，即 5 秒、25 秒、125 秒……这套复习间隔与其基于音频的语言学习程序相结合，形成了 Pimsleur 方法。然而，由于这套复习周期是预先录制的，其无法适应学习者的实际能力和材料的实际难度。例如，一个中国学生可能会非常容易地记住 apple，但很难记住 archaeology。但在 Pimsleur 方法中，他必须按照固定的、以相同速度增长的复习间隔来复习这两个单词。

2.2.2 Leitner 系统

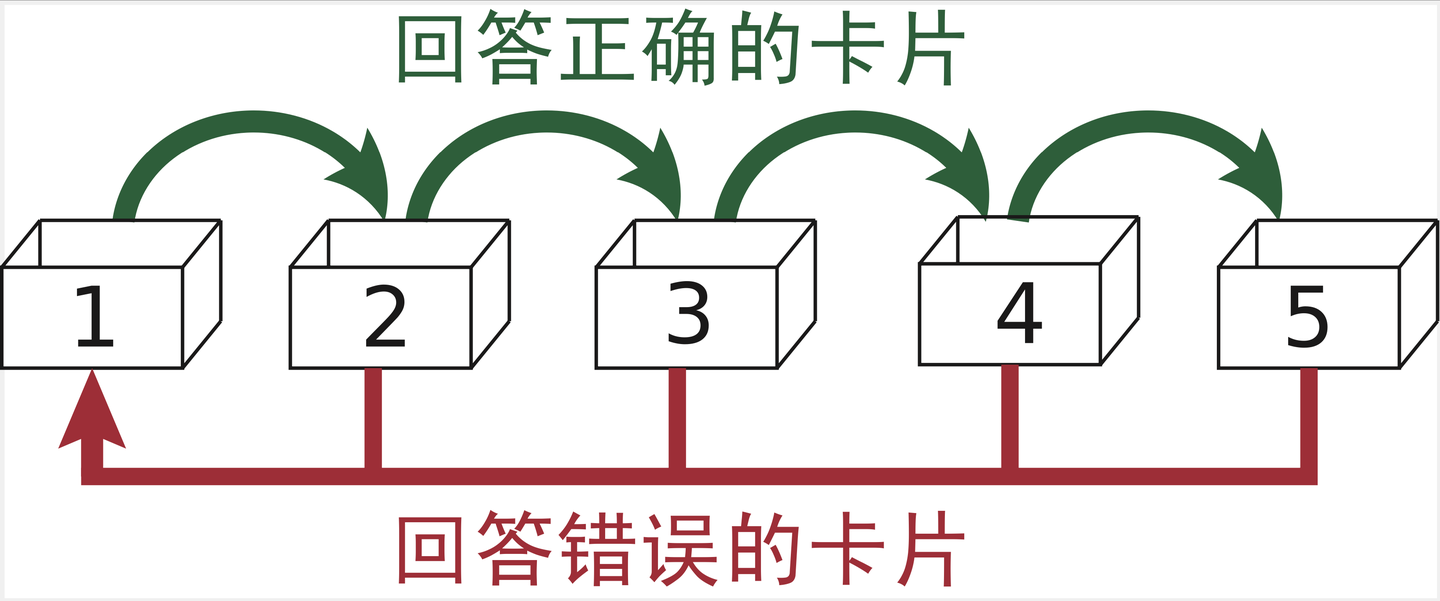
Leitner 提出了一种基于纸质抽认卡和盒子的间隔重复调度算法——Leitner盒子[21]。通过将卡片在代表不同熟练度的盒子之间进行转移，加上为不同盒子安排不同的复习周期，Leitner 盒子表现出更强的适应能力。目前依然有不少基于 Leitner 盒子的间隔重复软件，并对其进行了改进。最常见的 Leitner 盒子变体是，准备若干个盒子，对应不同的复习间隔，如“1 天”、“2 天”、“4 天”……。所有的抽认卡会先放入“1 天”的盒子内容。然后每天学习者需要复习“1 天”盒子内容的卡片，并对每张卡片进行反馈。记住的卡片将会被放入“2 天”的盒子。学习者每两天复习一次“2 天”盒子，每四天复习一次“4 天”盒子。在复习过程中被忘记的卡片将会被放回“1 天”盒子，如图 2-1 所示。用同样的例子来说明，2.2.1 节中的中国学生可能会因为记不住 archaeology 而将记有该单词的卡片放回“1 天”盒子，相比 apple 进行更频繁的复习。

2.2.3 SuperMemo 2 算法

Wozniak 提出了首个运行于计算机的间隔重复算法 SM-2[22]，其通过学习者对记忆的评分来评估电子抽认卡的难易程度，然后基于难易程度和学习者的评分来计算复习间隔。

SM-2 的伪代码如算法 2-1 所示，其中表示学习者对此次复习的评分，范围为 0～5，大于等于 3 视为回忆成功。 $n$ 表示学习者连续回忆成功的次数。I 表示学习者复习的间隔。EF 表示该记忆内容的简易程度。根据 SM-2 模型，可以得出一个重复的间隔序列：1 天、6 天、15 天、38 天……以此类推。如果学习者在复习过程中遗忘，间隔将重新从 1 天开始。并且由于简易度的下降，新的间隔序列整体短于上一次的序列，从而让学习者对每张抽认卡的回忆概率逐步提高，直到学习者能较大概率回忆起这些抽认卡。

SM-2 模型将学习者的复习间隔和回忆评分作为输入，引入简易度作为中间变量，通过硬编码的模型计算下一次间隔，实现了对不同抽认卡的独立跟踪和间隔安排。该模型的优点在于部分考虑了记忆行为的序列特征。其局限性在于，由于模型是根据经验硬编码的，不能定量地预测学习者的遗忘情况。并且模型对简易度的迭代调整较小，导致间隔的收敛速度也较为缓慢。

2.2.4 Memorize 算法

Tabibian 等人[23]引入了标记的时间点过程来表示间隔重复，并将调度视为一个最佳控制问题。

$\begin{aligned} m_\mathrm{i}(t)&=\mathbb{P}(r)=\exp (-n_\mathrm{i}(t)(t-t_\mathrm{r}))\\ \mathrm{d} n_\mathrm{i}(t)&=-\alpha_\mathrm{i} n_\mathrm{i}(t) r_\mathrm{i}(t) \mathrm{d} N_\mathrm{i}(t)+\beta_\mathrm{i} n_\mathrm{i}(t)(1-r_\mathrm{i}(t)) \mathrm{d} N_\mathrm{i}(t)\\ \mathrm{d} m_\mathrm{i}(t)&=-n_\mathrm{i}(t) m_\mathrm{i}(t) \mathrm{d} t+(1-m_\mathrm{i}(t)) \mathrm{d} N_\mathrm{i}(t) \end{aligned}$ (2-9)

式中

$m_\mathrm{i}(t)$ ——— $t$ 时刻项目 $i$ 的回忆概率；

$t-t_\mathrm{r}$ ———上次复习的时间点;

$n_\mathrm{i}(t)$ ——— $t$ 时刻项目 $i$ 的遗忘率；

$N_\mathrm{i}(t)$ ——— $t$ 时刻项目 $i$ 的复习次数；

$\alpha_\mathrm{i}$ ———回忆成功时遗忘率的变化率；

$\beta_\mathrm{i}$ ———回忆失败时遗忘率的变化率；

通过使用带跳变的随机微分方程刻画记忆的动态，Memorize 算法提出了以下优化目标，并应用随机最优控制的方法解决：

$\ell(m(t), n(t), u(t))=\frac{1}{2}(1-m(t))^{2}+\frac{1}{2} q u^{2}(t)$ (2-10)

式中

$q$ ———权衡回忆概率和复习次数的参数；

$u$ ———复习强度；

结合最小化遗忘率和复习强度与记忆系统动态，Memorize 调度算法在一定程度上拥有了处理间隔重复过程中时序信息的能力。但其系统动态没有考虑每次复习之间的间隔对遗忘率的影响。

2.2.5 基于强化学习的方法

一些论文[14, 24-26]通过设计奖励和在模拟环境中的训练，使用 RL 来最大化学习者的记忆期望。通用的马尔科夫决策过程的优化问题可以表述如下：

$\pi^{*}=\underset{\pi \in \Pi}{\operatorname{argmax}} \mathbb{E}_{s_{0}, a_{0}, \ldots}\left[\sum_{t=0}^{\infty} \gamma^{t} R(s_{t}, a_{t}) \mid \pi\right]$ (2-11)

式中

$\pi$ ———策略；

$R$ ———奖励函数；

$s$ ———状态；

$a$ ———行动；

$\gamma$ ———衰减系数；

在间隔重复中，状态即学习者此刻的所有记忆状态，行为则是此刻选择哪些记忆进行复习巩固。而奖励函数通常被定义为当前所有记忆的回忆期望。最优的间隔重复策略旨在最大化所有记忆的回忆期望。

2.3 循环神经网络

2.3.1 简单循环网络

现实中很多任务的输入在时间上不是独立的，比如语音、语言，并且这些任务的时序数据长度通常是不固定的。传统的前馈网络难以解决这些问题，于是循环神经网络运用而生。循环神经网络中的神经元同时接受其他神经元和自己过去的信息，形成了带环的网络结构，这赋予了循环神经一定的短期记忆能力。在间隔重复中，同一位学习者对同一条材料在不同时刻的复习之间是不独立的，循环神经网络正适合用于这种场景。通过输入记忆行为时序数据，循环神经网络可用于预测记忆的状态变化。

如图 2-2 所示，一个简单的 RNN 是在一个两层的前馈神经网络中加入一个隐藏层实现的。除了相邻的层之间有连接，隐藏层自身到自身也存在反馈连接。这使得当前时刻的隐藏层状态不仅与当前时刻的输入有关，也与上一时刻的隐藏层状态相关。

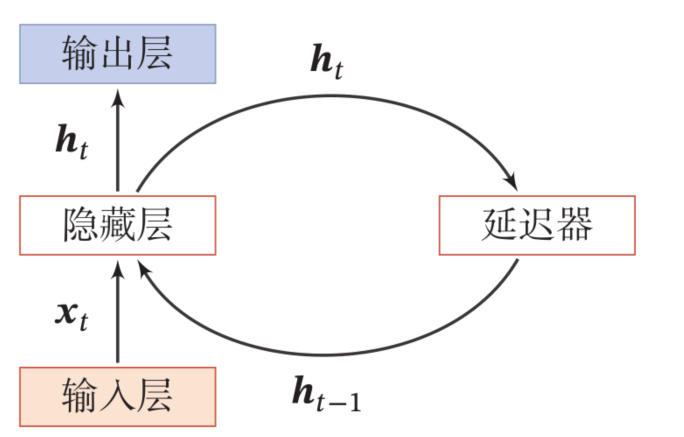
尽管 RNN 可以学习使用过去的相关信息，但在实践中，它们很难捕获长程依赖关系。为了改善该问题，引入门控机制来控制信息在循环中的积累与遗忘，是一个很好的解决方案。长短期记忆网络[27]和门控循环单元网络[28] 是这类方案的常见实现。

2.3.2 长短时记忆网络

LSTM 的整体链状结构非常类似于 RNN，但 LSTM 中单元的内部结构比 RNN 中单元的内部结构稍微复杂一些。LSTM 专门通过引入新的内部状态 c 进行线性循环信息传递，同时非线性地将信息输出到隐藏层。同时，LSTM 使用门控机制来控制信息传递的路径，包括遗忘门、输入门、输出门，每个门都有各自的用途。遗忘门确定前一存储单元的哪个部分应该被带到下一步，而输入门决定哪些值将被更新。输出门确定单元状态的哪些部分应该提供输出。

在 RNN 中，历史信息被存储在隐藏层的状态 h 中，并在每个时刻被更新，所以它可以被视为一种短期记忆。相比之下，神经网络的网络参数隐含了从训练数据中学到的经验，可以被视为一种长期记忆。LSTM 能够捕获长短期记忆的原理是，关键信息能被记忆单元 c 保存一段时间，其存续期短于长期记忆，又长于短期记忆 h。

2.3.3 门控循环单元网络

GRU 是 RNN 的另一种类型，也具有门控体系结构。它具有通过将遗忘门和输入门组合而形成的更新门。相比 LSTM，GRU 还有一些额外的变化，如单元状态 c 和隐藏状态 h 的整合。GRU 的结构相比 LSTM 更为简单，同时也改善了 RNN 的长程依赖问题。

2.4 随机最优控制

2.4.1 确定性问题的动态规划

对于一个离散时间的动态系统，每个时刻的系统状态与上一时刻的状态和决策有关。可用一个函数来描述系统动态特性。已知系统初始状态、系统动态特性和决策序列，就可以计算出任意时刻的系统状态变量[29]2-4。

在动态系统的发展过程中，系统的使用者往往有所期待。例如，对于间隔重复系统，学习者希望自己记忆材料付出的时间最少。通过引入代价函数来描述成本与系统状态、决策之间的关系，然后对每个时刻的代价进行累加，可得到总的代价值。描述总代价的函数即确定性问题的目标函数。对于动态规划可求解的问题，需要代价函数只依赖于当前时刻的状态和决策，以满足最优性原理。对于确定性系统，动态规划将求解每一个状态下的最优决策量，以最小化目标函数。

2.4.2 随机性问题的动态规划

然而，在间隔重复中，学习者的记忆反馈存在随机性，因此间隔重复系统是一个有随机性的动态系统。针对具有随机性的动态系统，动态规划将求解一个最优策略而非给出决策量的值。同时，在计算每个状态的最优策略时，随机性问题的目标函数是带期望的[29]14-16。

2.4.3 无限阶段问题的动态规划

考虑到记忆的随机性，无法保证记忆的状态能够在有限阶段内达到学习者期望的目标。因此，该对动态系统进行控制最优化需要考虑无穷多阶段的问题。这要求在动态规划求解过程中，需要遍历所有状态值。通过使用分布式异步值迭代方法，每次只需要更新一个状态对应的值函数，也能让值函数收敛到最优[29]197-200 。

2.5 本章小结

在优化间隔重复方面已经有大量的文献，从建模和预测学习者的长期记忆到基于相关记忆模型设计优化调度算法。

间隔重复和记忆模型。适应性思维特征-理性模型（Adaptive Control of Thought—Rational, ACT-R）[18]是一种认知体系结构，其包含了陈述性记忆模块，假设每次练习会尝试一条幂函数遗忘曲线，多个幂函数近似了间隔重复后的遗忘曲线。而多尺度语境模型（MCM）[19]，假设每次练习都会产生一条指数函数遗忘曲线，使用多个指数函数叠加来近似遗忘曲线。半衰期回归模型（HLR）[12]是一个可训练的间隔重复模型。为了预测学习者对特定材料的记忆半衰期，在线语言学习平台 Duolingo 的研究者使用他们的学习者日志数据进行训练。Ahmed Zaidi 等人[13]在该模型上进行了改进，将神经网络引入了该模型，并考虑了更多心理学、语言学相关的特征。但这些模型没有考虑学习者对单词记忆的反馈顺序和反馈之间的间隔，缺失了时序信息。

用间隔重复模型进行优化调度。为了平衡新材料的学习和已学材料的复习， Reddy 等人[30]提出了 Leitner 系统[21]的排队网络模型，并设计了一种启发式算法来安排复习。然而，该算法是基于 EFC 模型[30]，将记忆强度作为复习次数和 Leitner 箱位置的函数，而不是重复之间的间隔。Tabibian 等人[23]引入了标记的时间点过程来表示间隔的重复，并将调度视为一个最佳控制问题。他们想出了回忆概率和复习数量之间的权衡。由于数据集的限制，他们模型中的遗忘率只受回忆结果的影响。在 Hunziker 等人[31]的工作中，优化间隔重复的调度归结为随机序列优化问题。他们设计了一种贪婪的算法来实现学习者保持率最大化的高性能。但该算法实现高效用的充分条件很严格，可能在大多数情况下不适用。最近，强化学习也被应用于优化间隔重复的安排。一些论文[14,24-26]通过设计奖励和在模拟环境中的训练，使用 RL 来最大化学习者的记忆期望。然而，他们的算法所基于的环境过于简化，使得它不能很好地适用于现实世界。除此之外，这些算法缺乏可解释性，在不同的模拟环境中，它们的表现也不尽相同，并不总是优于启发式算法。

循环神经网络和最优控制是解决间隔重复调度问题的合适工具。首先，循环神经网络在处理时序数据上有很大的优势，特别是在间隔重复中，人类的记忆变化不仅仅依赖于单次复习的结果，也与复习时的记忆状态有关。而循环神经网络通过将历史输入编码成一个隐含状态，新一时刻的输入与隐含状态共同决定了当前输出和新的隐含状态，与人类的记忆十分类似。其次，最优控制非常适用于有明确系统动态和优化目标的问题。在间隔重复中，记忆的动态变化可以由循环神经网络捕获，优化的目标则与学习者的实际需求相关。通过将间隔重复问题化为一个无限阶段的随机动态规划问题，最优控制能够给出可解释的解决方法。

第 3 章间隔重复调度算法构建方法

3.1 记忆预测：LSTM-HLR 模型

3.1.1 数据收集

本文收集了墨墨背单词一个月的日志，包含 2.2 亿条记忆行为数据，以建立一个模型来模拟学习者的记忆。由于以下原因，本文没有使用 Duolingo 的开源数据集：

它缺乏时间序列方面的内容，如反馈和间隔的序列，而本文对数据的分析表明，历史特征对记忆状态有很大的影响。
它的回忆概率定义存在问题。Duolingo 将回忆概率定义为一个单词在特定会话中被正确回忆的次数比例，这意味着同一单词在特定会话中的多次记忆行为是独立的。然而，第一次回忆会影响学习者的记忆状态和全天的后续记忆。

从墨墨背单词收集的记忆数据记录了学习者对单词记忆的历史信息。对于任意一个记忆行为，本文用一个四元组来表示：

$e :=(u, w, t, r)$ (3-1)

式中

$e$ ———记忆行为事件；

$u$ ———学习者；

$t$ ———学习发生的时刻；

$w$ ———学习的单词；

$r$ ———学习的反馈；

其含义为一名学习者 $u$ 在时刻 $t$ 回忆单词 $w$ 并反馈 $r$ （回忆成功 r = 1；回忆失败 r = 0）的事件。

为了便于研究记忆行为事件序列，本文将历史序列特征加入其中：

$e_\mathrm{i} :=(u, w, \bm{\Delta t_\mathrm{1:i-1}}, \bm r_\mathrm{1:i-1} , \Delta t_\mathrm{i} , r_\mathrm{i})$ (3-2)

式中

$e_\mathrm{i}$ ———学习者 $u$ 对单词 $w$ 的第 $i$ 次记忆行为事件；

$\Delta t$ ———学习者对同一个单词的两次相邻回忆事件之间的时间间隔；

$\bm \Delta t_\mathrm{1:i-1}$ ———第 1 次到第 i − 1 次回忆的间隔历史序列；

$\bm r_\mathrm{1:i-1}$ ———第 1 次到第 i − 1 次回忆的反馈历史序列；

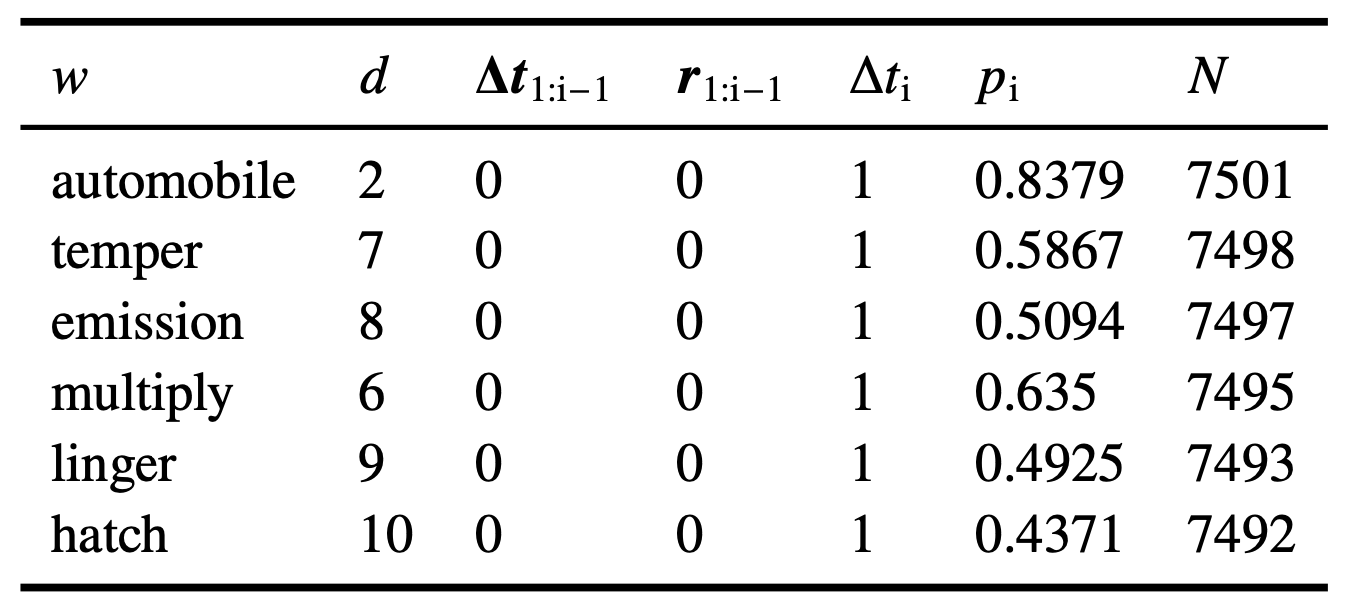
本文过滤掉其中第一个反馈为 r = 1 的日志，以排除学习者在使用间隔重复之前形成的记忆的影响。学习者的记忆行为事件的样本日志见表 3-1。

由此本文得到了包含任意学习者对任意单词的完整记忆行为历史数据。接下来，本文将基于该数据和遗忘曲线，从而引出本文对记忆半衰期的定义。

3.1.2 记忆半衰期

遗忘曲线是说，学习者停止复习后，记忆会随着时间的推移而衰退。在公式 (3-2) 定义的记忆行为事件中，回忆是二元的（即，学习者要么完全回忆起一个单词，要么忘记一个单词）。为了捕捉记忆的衰退，本文需要得到二元回忆背后潜在的概率。为了得到回忆概率，本文忽略学习者本身的影响，用学习该单词的学习者中的回忆比例 $\frac{n_\mathrm{r=1}}{N}$ 作为回忆概率 $p$ ，从而聚合得到：

$e_\mathrm{i} :=(w, \bm{\Delta t}_\mathrm{1:i-1}, \bm r_\mathrm{1:i-1}, \Delta t_\mathrm{i} , p_\mathrm{i}, N)$ (3-3)

式中

$p_\mathrm{i}$ ———有相同记忆行为历史下的学习者群体中的回忆成功比例；

$N$ ———拥有相同记忆行为历史下的学习者数量；

通过控制 $w$ 、 $\bm{\Delta t}_\mathrm{1:i-1}$ 和 $\bm r_\mathrm{1:i-1}$ ，绘制每个复习间隔 $\Delta t$ 对应的回忆概率 $p$ ，从而得到遗忘曲线。当 $N$ 足够大时，比例 $\frac{n_\mathrm{r=1}}{N}$ 接近回忆概率。然而，墨墨背单词中有将近 10 万个单词，在不同的时间序列中为每个单词收集的行为事件是稀疏的。本文需要对单词进行分组，以便在区分不同的单词和缓解数据稀疏性之间做出权衡。鉴于本文对遗忘曲线感兴趣，而材料的难度会明显影响遗忘速度。因此，本文尝试用第一次学习它们后第二天的回忆比例作为划分单词难度的标准。而图 3-1 (a) 描绘了数据集中回忆比例的分布。

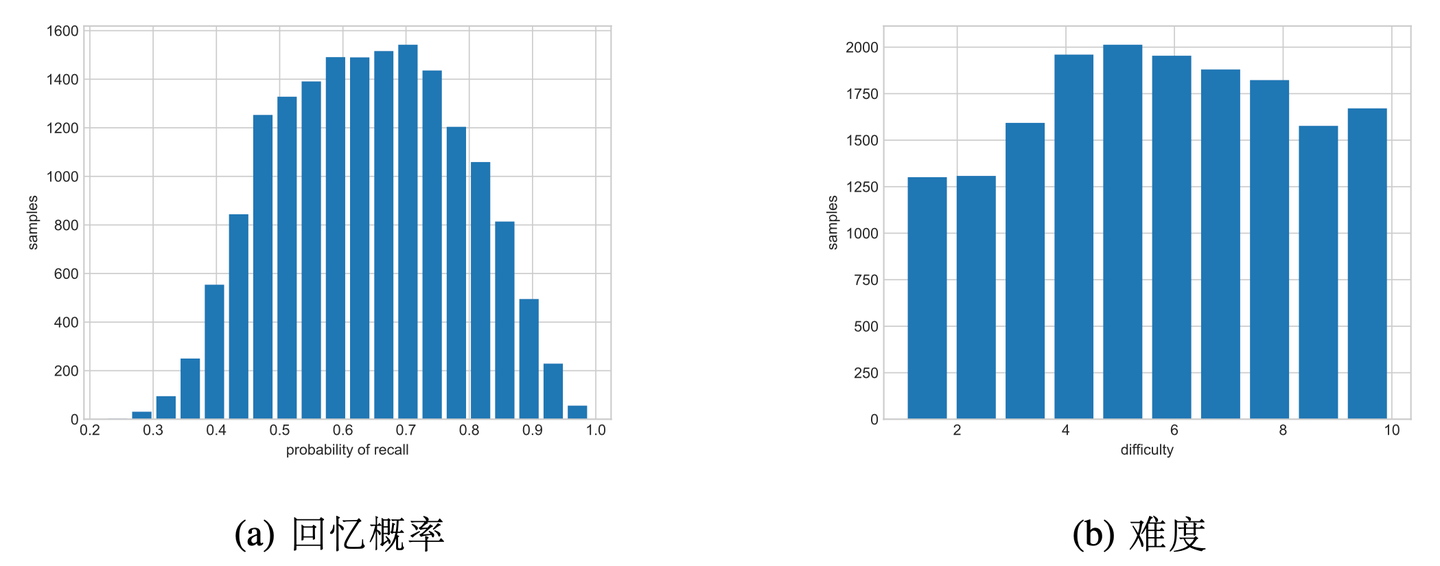
从数据分布中看到，回忆比例大多在 0.45 和 0.85 之间。为了使分组数据的平衡和密度，将单词分为 10 个难度组。分组的结果显示在图 3-1 (b) 和表 3-2 中。符号 $d$ 表示难度，数字越大，难度就越大。

使用分组后的数据，便可以绘制有足够数据支持的遗忘曲线。基于指数遗忘曲线模型 $p_\mathrm{i} = 2^{-\frac{\Delta t_\mathrm{i}}{h_\mathrm{i}}}$ 对其进行拟合，并由此得到记忆半衰期 $h_\mathrm{i}$ 。通过此方法，将 $\Delta t_\mathrm{i} , p_\mathrm{i}$ 特征降维得到 $h_\mathrm{i}$ ，再将聚合数据得到的回忆概率 $p_\mathrm{i}$ 按照时间顺序进行拼接，得到回忆概率序列 $\bm p_\mathrm{1:i-1}$ 作为特征之一。最终，数据实例为：

$e_\mathrm{i}:=(d, \bm{\Delta t}_\mathrm{1:i-1}, \bm r_\mathrm{1:i-1}, \bm p_\mathrm{1:i-1}, \Delta t_\mathrm{i} , p_\mathrm{i}, h_\mathrm{i})$ (3-4)

式中

$d$ ———单词难度分组；

$\bm p_\mathrm{1:i-1}$ ———第 1 次到第 i − 1 次回忆的回忆比例历史序列；

$h_\mathrm{i}$ ———学习者群体的记忆半衰期；

3.1.3 模型表示

本文采用了最简单 LSTM 网络，一层输入层、一层隐藏层、一层全连接层。网络的输入输出可描述如下：

$\hat{h_\mathrm{i}}=\mathrm{LSTM}(\bm{\Delta t}_\mathrm{1:i-1}, \bm r_\mathrm{1:i-1}, \bm p_\mathrm{1:i-1})$ (3-5)

式中

$\hat{h_\mathrm{i}}$ ———第 i 次回忆时的记忆半衰期预测值；

LSTM———LSTM 模型；

从由公式 (3-4) 定义的数据中取出 3 个通道时序特征用于训练 LSTM 网络，以拟合不同记忆行为历史下的记忆半衰期。模型的目标是降低记忆半衰期的预测误差，因此设置损失函数如下：

$l(e_\mathrm{i},\bm\theta)=|\frac{h_\mathrm{i}-\hat{h_\mathrm{i}}}{h_\mathrm{i}}|+C||\bm\theta||_{2}^{2}$ (3-6)

式中

$l$ ———损失函数；

$C$ ———正则化系数；

$\bm\theta$ ———模型权重；

之所以采用 h 的相对百分比误差作为损失项，是因为相同的绝对误差在不同的记忆半衰期上的代价是不同的。举例来说，10 天的绝对误差，对于一个真实半衰期为1天的记忆行为，将会导致回忆概率误差 $|p-\hat{p}|=|2^{-\frac{1}{1}}-2^{-\frac{1}{11}}|\approx 0.4389$ ，而对一个真实半衰期为 100 天的记忆行为，其导致的回忆概率误差 $p-\hat{p}=2^{-\frac{100}{100}}-2^{-\frac{100}{110}}\approx 0.0325$ 。

结合 2.1.5 节的 HLR 模型，对于任何一条数据实例，都可由下式预测学习者的回忆概率：

$\hat{p_\mathrm{i}}=2^{-\frac{\Delta t_\mathrm{i}}{\hat{h_\mathrm{i}}}}$ (3-7)

式中

$\hat{p_\mathrm{i}}$ ———第 i 次回忆时的回忆概率预测值；

3.2 复习规划：SSP-MMC 算法

3.2.1 问题设置

间隔重复方法的目的在于帮助学习者高效地形成长期记忆。而记忆半衰期反映了长期记忆的存储强度，复习次数、每次复习所花费的时间则反映了记忆的成本。所以，间隔重复调度优化的目标可以表述为：在给定记忆成本约束内，尽可能让更多的材料达到目标半衰期，或以最小的记忆成本让一定量的记忆材料达到目标半衰期。其中，后者的问题可以简化为如何以最小的记忆成本让一条记忆材料达到目标半衰期，即最小化记忆成本（Minimize Memorization Cost, MMC）。

本文在 3.1.3 节所构建的长期记忆模型满足马尔可夫性，每次记忆的状态只取决于上一次的记忆状态和当前的复习输入和结果。其中回忆结果服从一个与复习间隔有关的随机分布。由于记忆状态转移存在随机性，一条记忆材料达到目标半衰期所需的复习次数是不确定的。因此，间隔重复调度问题可以视作一个无限阶段的随机动态规划问题。考虑优化目标是让记忆半衰期达到目标水平，所以本问题存在终止状态，可以转化为一个随机最短路径问题[29]177-182（Stochastic Shortest Path, SSP）。结合优化目标，本文将算法命名为 SSP-MMC。

3.2.2 状态表示

为了解决转化为随机最短路径问题的间隔重复最小化记忆成本问题，首先要解决的是如何描述学习者长期记忆的系统动态。根据 3.1.3 节的 LSTM-HLR 模型，训练好的 LSTM 网络在预测记忆行为序列的记忆半衰期过程中，使用记忆单元 $\bm c_\mathrm{k}$ 和隐藏层 $\bm h_\mathrm{k}$ 来记录当前时刻的状态。根据网络结构，记忆单元和隐藏层的值只依赖于当前时刻的输入值和上一时刻自身的值。如果将记忆单元和隐藏层视作记忆状态，那么记忆状态 $\bm x_\mathrm{k}$ 和复习行为 $u_\mathrm{k}$ 之间的关系可用马尔可夫决策过程描述。

通过拼接记忆单元和隐藏层，记忆状态可描述如下：

$\bm x_\mathrm{k} = (\bm c_\mathrm{k},\bm h_\mathrm{k})$ (3-8)

式中

$\bm x_\mathrm{k}$ ———第 k 次复习时的记忆状态；

$\bm c_\mathrm{k}$ ———预测第 k 次复习时 LSTM 网络的记忆单元状态；

$\bm h_\mathrm{k}$ ———预测第 k 次复习时 LSTM 网络的隐藏层状态；

复习行为，即在此次复习后多少天再次复习，可描述如下：

$u_\mathrm{k}=\Delta t_\mathrm{k}$ (3-9)

式中

$u_\mathrm{k}$ ———第 k 次复习后规划的复习行为；

$\Delta t_\mathrm{k}$ ———第 k 次复习后规划的复习间隔；

随机变量，即每次复习时的结果，可描述如下：

$r_\mathrm{k} \sim B(p_\mathrm{k})$ (3-10)

式中

$r_\mathrm{k}$ ———第 k 次复习的回忆反馈；

$B$ ———伯努利分布；

$p_\mathrm{k}$ ———第 k 次复习的回忆概率；

每次复习后记忆状态的系统动态可描述如下：

$\bm x_\mathrm{k+1}=\mathrm{LSTM}(\bm x_\mathrm{k},u_\mathrm{k},r_\mathrm{k})$ (3-11)

式中

$\bm x_{k+1}$ ———记忆状态 $\bm x_\mathrm{k}$ 、复习行为 $u_\mathrm{k}$ 和记忆反馈 $r_\mathrm{k}$ 的下一个记忆状态；

通过引入决策成本和终止状态 $\bm x_N$ ，可得到图 3-2 描述的随机最短路径问题。图中的圆圈代表了记忆状态，方块是可选的复习行为，虚线箭头表示给定复习行为后的下一个记忆状态和转换概率，实线箭头表示给定记忆状态下可选的复习行为与相应的复习成本。通过计算不同记忆状态对应的记忆半衰期，可得到达到目标半衰期的记忆状态集合。该集合内的记忆状态节点即终止状态。而间隔重复中的随机最短路径问题是调度算法如何建议复习行为，以最小化达到终止记忆状态的期望复习成本。

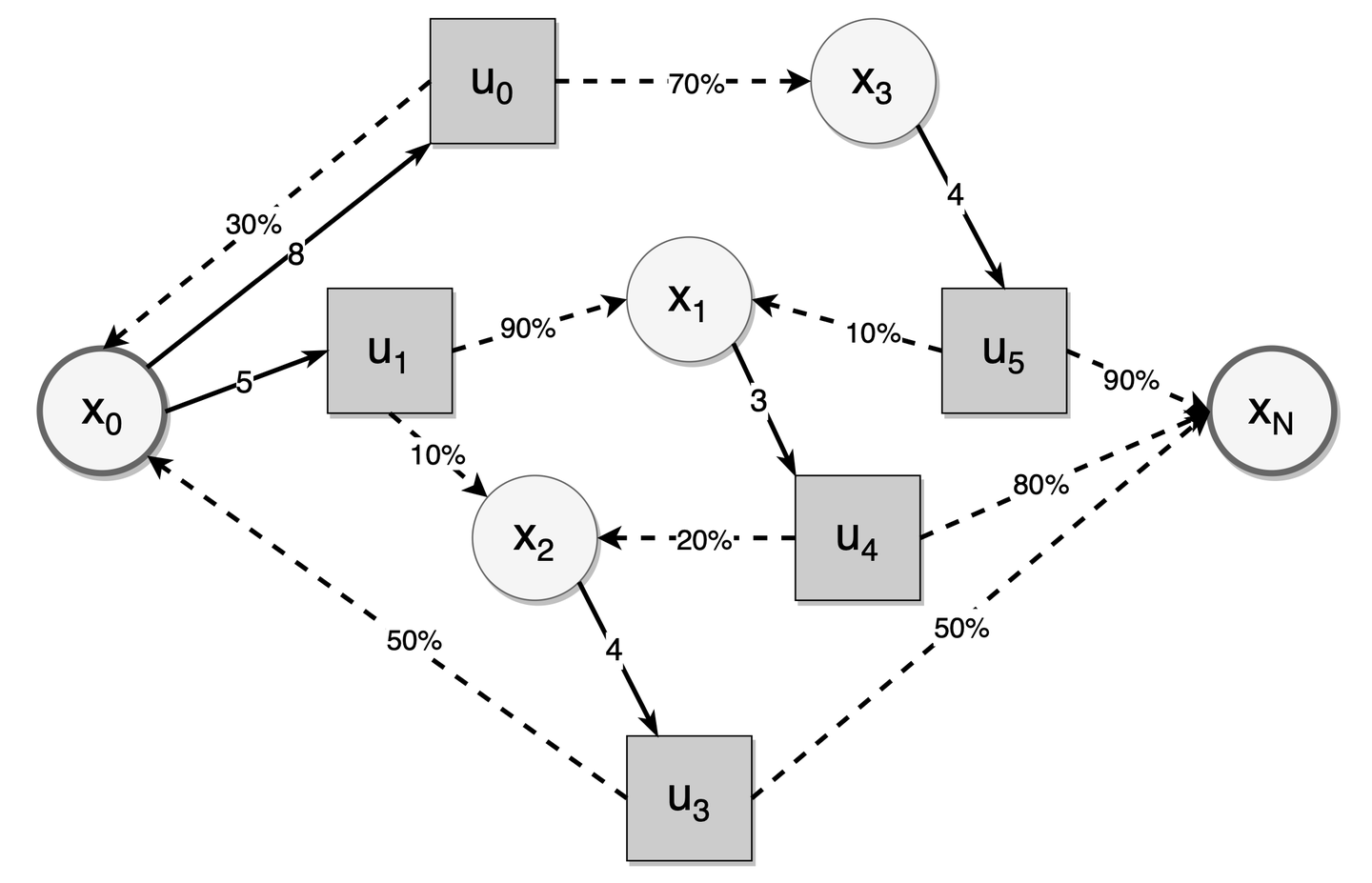
3.2.3 算法设计

根据马尔可夫决策过程的定义，SSP-MMC 的贝尔曼方程可设置如下：

$J(\bm x_\mathrm{k}) = \min\limits_{u_\mathrm{k} \in U_\mathrm{k}(\bm x_\mathrm{k})} E[g(r_\mathrm{k}) + J(\mathrm{LSTM}(\bm x_\mathrm{k},u_\mathrm{k},r_\mathrm{k}))]$ (3-12)

式中

$\bm x_0$ ———初始记忆状态；

$J$ ———记忆状态对应的复习总成本；

$U_\mathrm{k}$ ———记忆状态对应的可选复习行为集^[2]；

$g$ ———记忆状态和复习行为对应的复习代价函数^[3]；

基于该方程，可以使用动态规划迭代求解，得到每个 $\bm x_\mathrm{k}$ 对应的最优复习行为 $u_\mathrm{k}$ 。考虑到 $\bm x_\mathrm{t}$ 的向量值都是连续的，不利于使用矩阵记录状态空间，可以将其离散化：

$\bm X \xrightarrow[]{(\lfloor \frac{\bm x}{\varepsilon} \rfloor|\bm x \in \bm X)} \bm{\mathrm{X}}$ (3-13)

式中

$\bm X$ ———记忆状态空间；

$\bm{\mathrm{X}}$ ———离散化的记忆状态空间；

$\varepsilon$ ———离散化精度；

根据 LSTM 采用 $\mathrm{tanh}$ 作为激活函数，其输出值域为 (−1, 1)，因此离散化后的每一维的离散值是有限的，总计 $\lceil\frac{2}{\varepsilon}\rceil$ 个。建立一个成本矩阵 $J^{\lceil\frac{2}{\varepsilon}\rceil}$ ，并将每一项元素初始化为 $+\infty$ 。设置 $J[\bm{\mathrm{x_0}}] = 0$ ，然后开始遍历每个 $\bm{\mathrm{x}}$ ，从 $U(\bm{\mathrm{x}})$ 中遍历每个 $u_\mathrm{k}$ ，计算 $p_\mathrm{k}$ 、 $\bm{\mathrm{x}}_\mathrm{r=1}$ 、 $\bm{\mathrm{x}}_\mathrm{r=0}$ 。

$J[\bm{\mathrm{x}}] = \min\limits_{p_\mathrm{k}} [p_\mathrm{k} \cdot (g(1) + J[\bm{\mathrm{x}}_\mathrm{r=1}]) + (1-p_\mathrm{k}) \cdot (g(0) + J[\bm{\mathrm{x}}_\mathrm{r=0}])]$ (3-14)

式中

$p_\mathrm{k}$ ———回忆成功的概率；

$\bm{\mathrm{x}}_\mathrm{r=1}$ ———回忆成功后的记忆状态；

$\bm{\mathrm{x}}_\mathrm{r=0}$ ———回忆失败后的记忆状态；

通过公式 (3-14)，算法能迭代更新每个记忆状态对应的最优成本。再使用一个策略矩阵记录每个状态下最优的复习间隔，最终最优策略会在一遍遍迭代中收敛。

3.3 间隔重复模拟环境

为了验证本文的复习调度算法的有效性，本文基于 LSTM-HLR 模型构建了一个间隔重复模拟环境，用于比较不同复习调度算法的性能。在间隔重复模拟环境中，模拟学习者从一个单词集合中挑选回忆的对象，并根据 LSTM-HLT 模型来生成回忆结果和记忆状态。复习调度算法根据回忆结果和记忆状态来安排下一个复习时机。

模拟过程涉及两个维度，一个是日间，一个是日内。为了模拟学习者的备考期限和每日学习时间限制，环境限制了模拟进行的天数和每天用于复习和学习的时间。然而，由于回忆结果的随机性，复习调度也受回忆结果的影响，因此可能出现当日复习安排耗时超过每日时间限制的情况。为了尽量避免这种情况，在模拟过程中优先保证复习任务完成。当每日时间耗尽时，不论复习任务是否完成，都延迟到第二天进行。

模拟流程如算法 3-1 所示，其中 $student$ 表示学习者的记忆模型，会根据复习情况更新记忆状态。 $scheduler$ 是间隔重复算法调度器，根据学习者反馈的记忆状态调整复习间隔。 $day_{limit}$ 是复习天数限制，可理解为学习者参与测试前可用于复习的天数。 $cost_{limit}$ 是每日复习成本限制，即学习者每天最多可用于复习的时间。

3.4 间隔重复系统架构

为了让本文的算法能够被应用于实际环境，本文设计了一套间隔重复系统架构。将数据集构建模块、记忆预测模块、复习调度模块相结合，可以得到端到端的间隔重复系统。由于这些模块对存储和算力的要求很高，所以本文将整个间隔重复系统拆分为远程和本地两个部分。

图 3-3 展示了间隔重复系统的框架，它分为两个主要部分：绿色为本地，红色为远程。

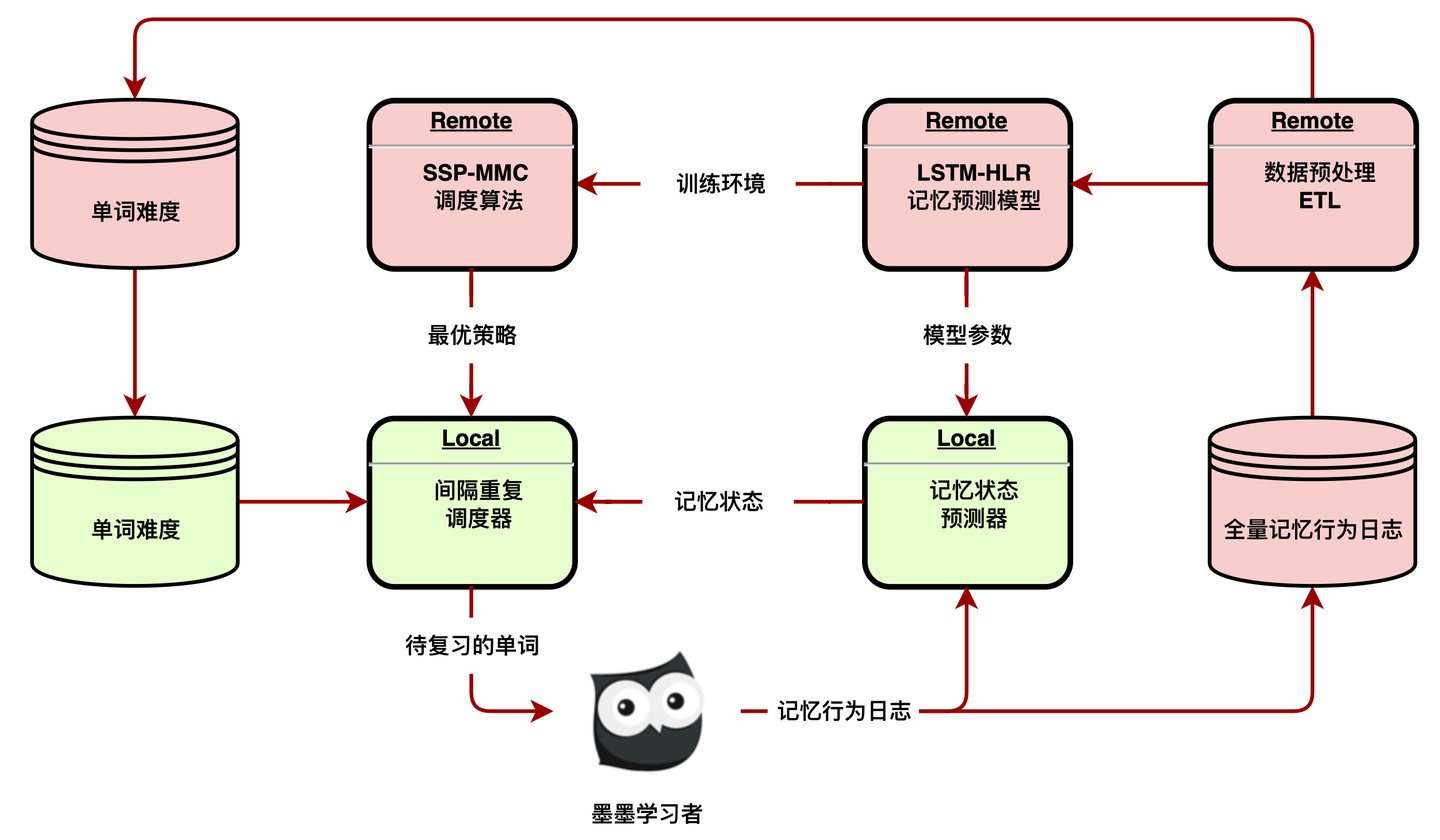
每次学习者复习单词时，带有时间序列信息的记忆行为事件将被记录在本地，本文称之为记忆行为日志。在学习者完成当天的所有复习后，这些日志会被上传到远程。完整的记忆行为日志必须处理大量的写入，需要永久保留，而且一旦写入就不会更新，所以本文使用流式数据服务将日志写入数据仓库。在预处理 ETL 中，定期计算所有单词的难度，并汇总 LSTM-HLR 记忆模型所需的训练数据，为 SSP-MMC 调度算法提供训练环境。在计算出模型参数和最优策略后，远程将相关配置推送到本地。然后本地预测器和调度器将加载新的配置来预测记忆状态，并为学习者学习的每个单词安排复习日期。通过将训练任务全部部署至远程，该框架对学习者的设备要求较低。同时，配置推送可以按一定的周期进行，不需要实时同步，对服务器的并发处理能力要求不高。

3.5 本章小结

本章依次介绍了记忆预测模型、复习规划算法、间隔重复模拟环境和间隔重复系统架构。

在记忆预测模型中，为了解决目前开源数据集缺少时序特征对问题，本文构建了新的记忆行为数据架构，尽可能包含完整的记忆行为序列信息。然后将常见的循环神经网络 LSTM 引入至 HLR 模型来估计记忆半衰期。在复习规划算法中，本文提出了最小化记忆成本的优化目标，并将间隔重复转化为一个随机最短路径问题。通过使用 LSTM-HLR 预测记忆系统动态，结合分布式异步值迭代方法，提出了 SSP-MMC 算法来计算每个记忆状态下最佳的复习行为。在间隔重复模拟环境中，本文将 LSTM-HLR 作为学生模型，并构建了每日学习成本限制和学习期限限制，以在相同的环境下对比不同复习算法的性能表现。在间隔重复系统架构中，为了使复习调度算法能够应用于现实环境中，本文拆分了算法训练和算法调用，将两者分布部署至远程和本地，以降低对客户端和服务端的性能要求。

第 4 章间隔重复系统实验

4.1 数据集构建

本实验收集了 1 个月的墨墨背单词学习者学习日志，其包含 2.2 亿条记忆行为数据。数据集构建过程如下：

一位学习者对一个单词的一次复习将产生一条记忆行为数据。其字段包括单词 id、学习者 id、时间戳、反馈；
当学习者完成当日的学习任务后，当日所有的记忆行为数据将以日志的形式上传至服务器；
在服务器上，日志同步系统将学习者学习日志结构化，写入数据库；
按照学习者和单词进行分组，计算每次复习之间的间隔。并将每次的反馈和间隔按先后顺序拼接，得到反馈序列和间隔序列；
按照单词难度、反馈序列、间隔序列分组，计算不同间隔下的回忆概率。并将每次复习的回忆概率按先后顺序拼接，得到回忆概率序列；
为了获得每个难度的单词在不同记忆行为历史下的半衰期和回忆概率，本实验对数据进行了聚合，最终得到 1.5 万条复习记录。

4.2 模型对比与评估指标

4.2.1 记忆预测模块

本实验采用了两个指标进行综合比较：

MAE(p)：计算预测的回忆概率与实际统计的回忆概率之间的绝对误差。回忆概率是一个落在区间中的连续值，MAE 越小，预测越准确；
MAPE(h)：计算预测的记忆半衰期与实际半衰期之间的绝对百分比误差。之所以对记忆半衰期不使用 MAE 而使用 MAPE 评估，是因为考虑到半衰期的现实意义。偏差 10% 和偏差 10 天，对于 1 天的半衰期和 100 天的半衰期而言，前者更符合实际。

本实验对比三类间隔重复模型及其变体：

LSTM-HLR，本文在3.1.3节所描述的模型。为了进行消融实验，考虑了 4 种变体：有和没有 $\bm{\Delta t}_\mathrm{1:i-1}$ 特征(+t)，以及有和没有 $\bm p_\mathrm{1:i-1}$ 特征 (+p)；
HLR，遗忘预测模型的对比基线，考虑两种变体：有和没有单词特征 (+l)；
SM-2，传统的启发式模型，与算法 2-1 中描述一致。

4.2.2 复习调度模块

本实验将 SSP-MMC 与几个基线调度算法进行对比：

Random 策略，每次从 [1, $h_N$ ] 中随机选择一个间隔进行安排复习。
Anki，SM-2 的一种变体开源算法。由于Anki的算法中，学习者的回忆结果是以 1-4 分输入。本文将回忆失败映射到 1 分，回忆成功映射到 3 分。
半衰期，即直接以半衰期作为本次安排的复习间隔。
固定阈值，即当小于等于某一水平（本实验使用 80%）时进行复习。
Memorize[23]，一种基于最优控制的算法，代码来自于他们开源的仓库。

本实验的评价指标包括：

达到目标半衰期的记忆数量（target half-life reached, THR）
累计记忆期望（summation of recall probability, SRP）
累计新增的记忆数量（words total learned, WTL）

4.3 实验流程

4.3.1 实验步骤

第一步，使用构建好的数据集来训练记忆预测模型，得到 LSTM-HLR。

第二步，为了确定合适的隐藏层节点数量，实验对比了不同节点数的误差情况，以确定 SSP-MMC 的状态空间维数。

第三步，训练 SSP-MMC 得到最优复习调度策略，其中 LSTM-HLR 作为状态转移函数调用。

第四步，使用 LSTM-HLR 搭建了一个复习模拟环境，模拟 SSP-MMC 和几个对比算法的复习情况，以评估算法效果。

4.3.2 LSTM-HLR 训练

本实验随机抽取 20% 的数据用于训练，最终确定了以下参数：迭代次数=500000，学习率=0.0005，权重衰减系数=0.0001，隐藏层节点数=16。HLR 模型的参数使用相同的数据进行训练，确定了以下参数：迭代次数=7500000，学习率=0.001， $\alpha$ =0.002， $\lambda$ =0.01。SM-2 模型不需要训练。对于剩余的 80% 数据，使用 5 次重复的 2 折交叉验证[32]进行评估。

4.3.3 损失函数对比

不同的损失函数，对记忆半衰期和回忆概率的预测结果可能会有较大的影响，本实验对比了 MAPE 和 L1 两类损失函数，以验证本文对损失函数的假设。

4.3.4 状态空间维度选择

随着隐藏层节点数量提高，SSP-MMC 的状态空间大小呈指数级增长。由于 SSP-MMC 的训练时间复杂度为 $\mathrm O(k\lceil\frac{2}{\varepsilon}\rceil^n)$ ，如果状态空间的维数过高，SSP-MMC 将无法在合理的时间内计算出结果。因此，研究状态空间维数与预测误差之间的关系，有助于挑选合适的隐藏层节点数量，以在预测精度与训练难度之间取得平衡。

4.3.5 SSP-MMC 训练

算法 4-1 描述了 SSP-MMC 的训练流程，其中 a 是回忆成功的复习成本，b 是回忆失败的复习成本， $x_N$ 是记忆的目标状态。 $\pi$ 是用于存储每个记忆状态下当前最优的复习间隔的矩阵。J 是是用于存储每个记忆状态下当前最优的复习成本的矩阵。

4.3.6 复习模拟

本实验设定 360 天（接近一年）的回忆半衰期为目标半衰期，当材料的记忆半衰期超过这个值时，它将不会被安排复习。然后，考虑到实际场景中学习者每天的学习时间大致恒定，本实验设定 600 秒（10 分钟）为每天学习成本的上限。当每次学习和复习过程中的累计成本超过这个上限时，无论是否完成，复习任务都会被推迟到第二天，以确保每种算法在相同的记忆成本下进行比较。本实验使用学习者的平均时间，即成功回忆的时间为 3 秒，失败回忆的时间为 9 秒。最后，语言学习是一个长期的过程，本实验设定模拟时间为 360 天。

4.4 本章小结

本章介绍了间隔重复系统实验的整体流程，其分为长期记忆预测模型 LSTM-HLR 训练和复习规划算法 SSP-MMC 训练。在长期记忆预测模型的训练中，本实验对比了不同损失函数对最终指标的影响，并探究了 LSTM 隐藏层节点数与误差降低的相对趋势。在复习规划算法的训练中，本实验基于 LSTM-HLR 模型，构建了一个间隔重复复习模拟环境，为 SSP-MMC 提供训练所需要的反馈。

第 5 章实验分析与讨论

5.1 长期记忆预测结果

表 5-1 展示了 SM-2、HLR、LSTM-HLR 以及对应消融实验的结果。图 5-1 展示了各模型的预测分布情况。

通过观察表 5-1 看到，同时带有 p 和 t 特征的 LSTM-HLR +p +t 模型表现最好；其次是只带 p 特征的 LSTM-HLR +p。并且，使用时序特征的所有模型在所有指标上都优于只使用统计特征的 HLR。本文认为这样的结果是基于一个事实：一个学习者连续记住同一内容三次再连续遗忘同一内容三次，与先连续遗忘三次再连续记住三次，这两个过程是截然相反的。HLR 仅考虑了历史累计正确次数和遗忘次数，无法区分这两个过程，只能在训练过程中给出折衷的预测，误差较大。

观察图 5-1 (a)至 5-1 (f) 的柱状图，可以看到记忆半衰期分布集中在 1 天至 10 天。通过对比各模型的 MAPE(h) 分布，可以发现 LSTM-HLR 系列模型在短半衰期区间的 MAPE(h) 明显小于 HLR 系列模型。本文认为这是 HLR 的损失函数公式 (2-8) 中的项所致。该项无差别地惩罚任意半衰期区间的误差，从而使低半衰期区间的百分比误差很大。本文的 LSTM-HLR 模型通过改进损失函数克服了这个问题。虽然在长半衰期区间上，HLR 系列模型的误差低于 LSTM-HLR 系列模型。但长半衰期区间的样例较少，对最终平均误差的影响较小。从现实角度来看，当记忆半衰期变长，学习者在下一次复习之前在背单词 APP 外进行学习的可能性越来越大，本文能收集到的记忆行为数据也会偏离学习者的真实情况。对于这些有偏差的数据，做出更准确预测的实际意义较小。

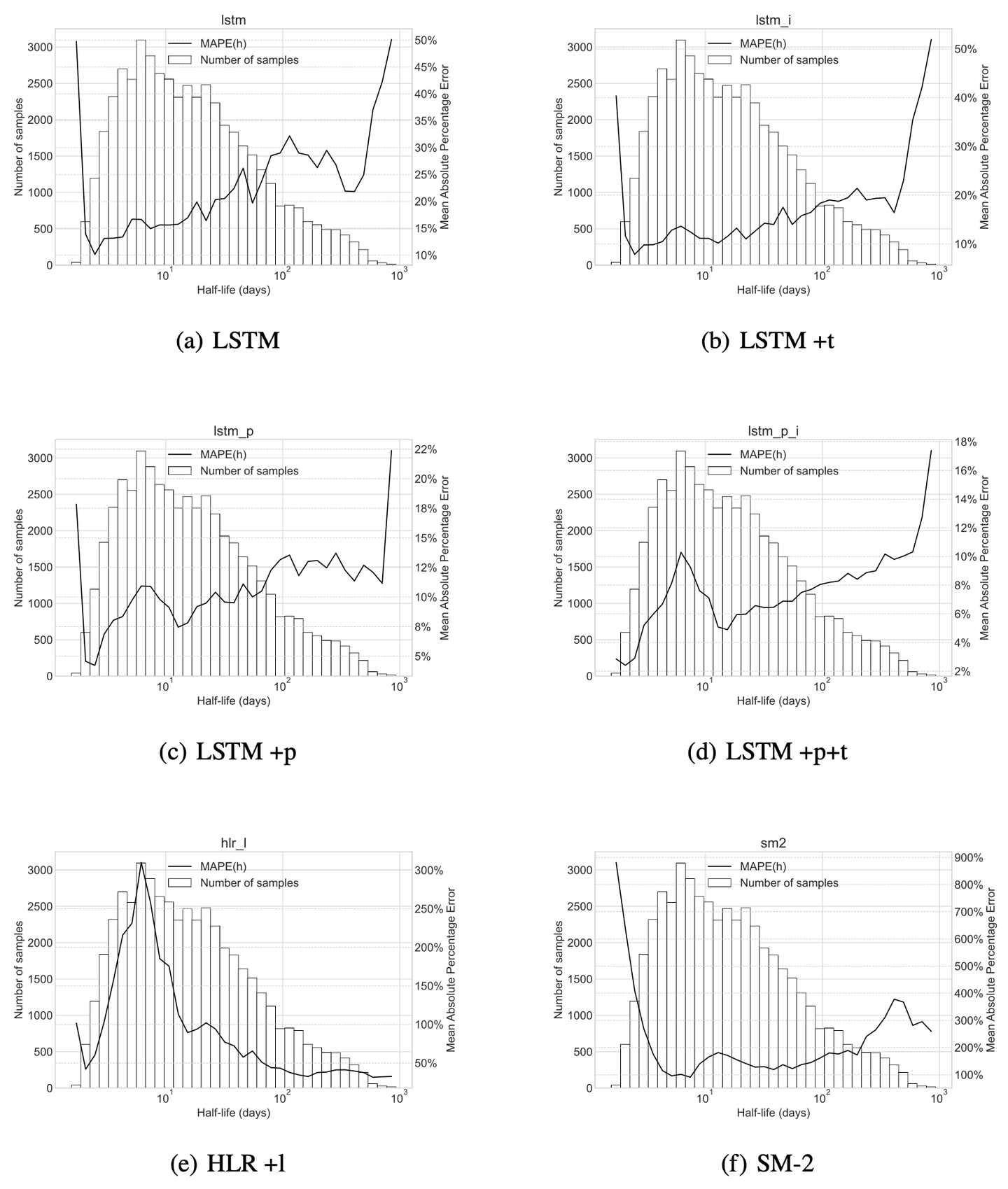
关于特征为何能降低预测的误差，本文认为这与心理学中记忆的提取强度与存储强度有关。较难提取的记忆经回忆会得到更多的强化[33]。在本文的模型中，历史的回忆概率可以反映出每次回忆的提取强度，而半衰期则类似于存储强度。因此，回忆概率历史对预测半衰期是有用的。

每次复习之间的间隔也是一个重要的信息。以(0-2-4-6-8)的间隔复习，与以(0-5-5-5-5)的间隔复习，效果会有显著的不同[34]，这一点在本文的实验中也得到了印证。

5.2 损失函数对比结果

表 5-2 展示了 MAPE 和 L1 二者作为 LSTM-HLR 损失函数后预测误差的结果。图 5-2 展示了预测误差的分布情况。

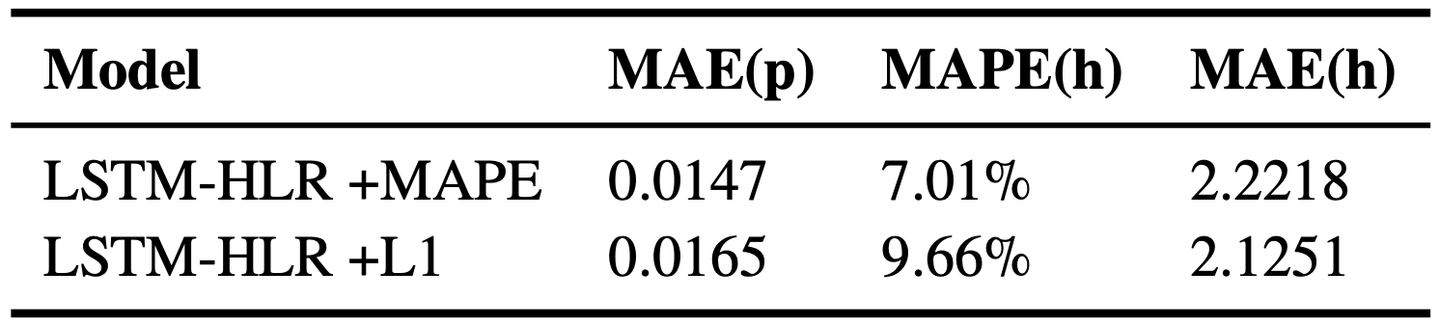
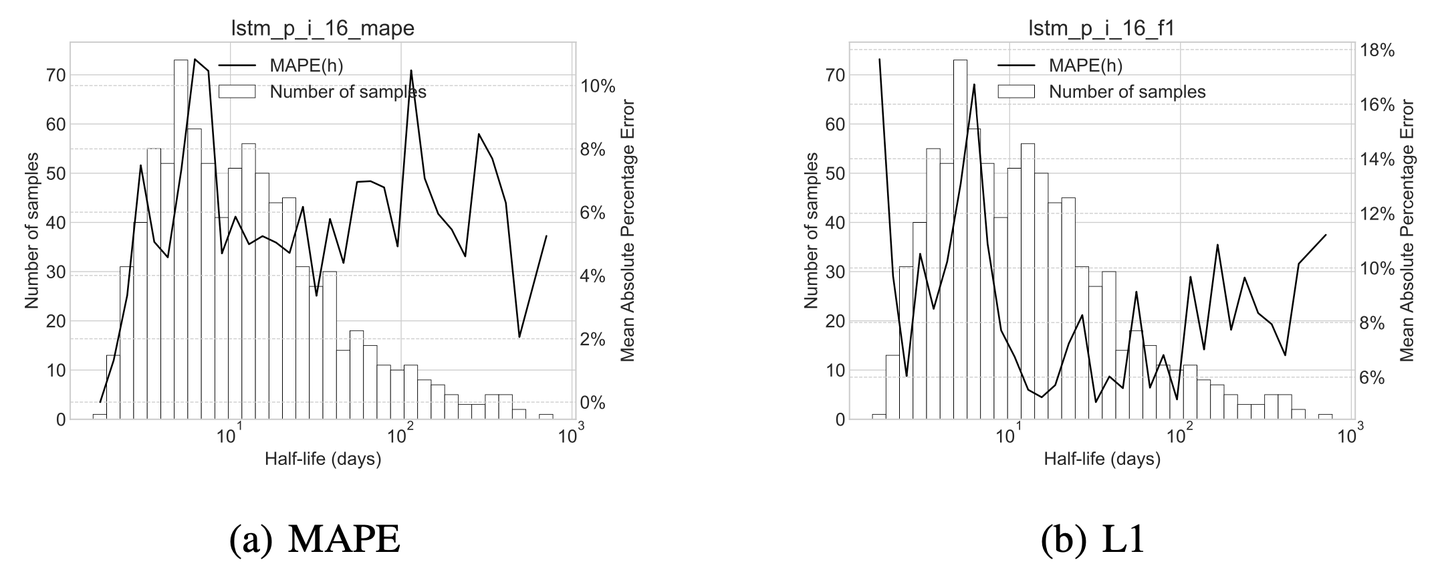
从表 5-2 中可以看出，虽然 LSTM-HLR +L1 在 MAE(h) 的误差上要低于 LSTM-HLR +MAPE，但其在 MAE(p) 上的误差依然高于 LSTM-HLR +MAPE。这可以由图 5-2 (a) 和图 5-2 (b) 之间的差异来解释。LSTM-HLR +L1 的误差主要集中在记忆半衰期 [0, 10] 的区间内，而这正是因为 L1 损失函数在惩罚误差时，不考虑记忆半衰期的相对大小。LSTM-HLR +MAPE 在这一区间内的误差则都小于 10%，虽然其在记忆半衰期为 $10^3$ 左右时的误差较大，但这一区间的样本较少，对总体而言影响不大。

5.3 状态空间维数选择结果

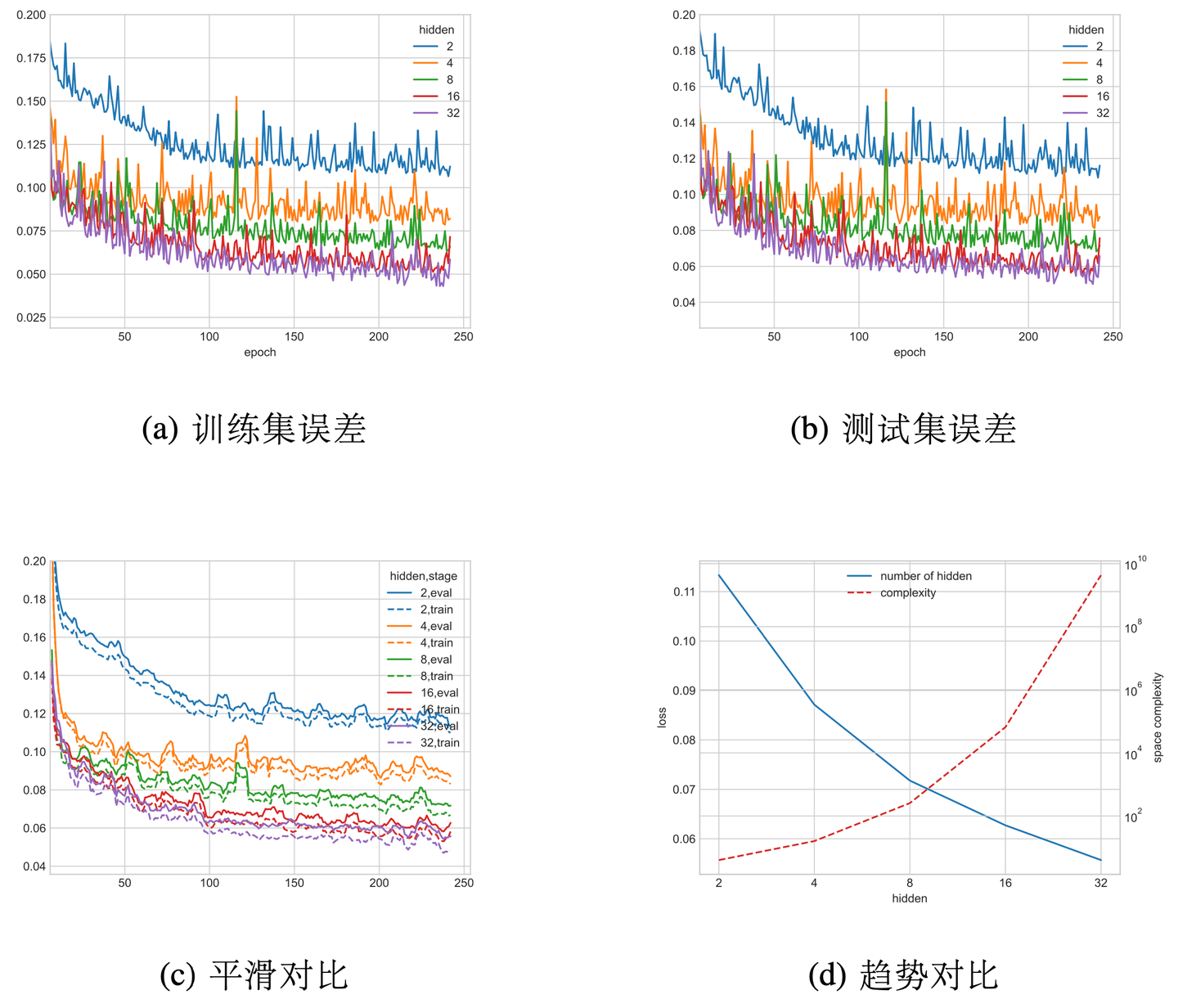
实验对比了 2、4、8、16、32 个隐藏层节点的效果，如图 5-3 所示。增加隐藏层节点数会指数级提高状态空间大小，提高复习调度算法的复杂度。而减少隐藏层节点数会提高长期记忆预测的误差。经过权衡，本文将隐藏层节点数固定为 4。

5.4 复习规划模拟结果

图 5-4 展示了模拟环境下各复习规划算法的表现。在指标 THR 上（图 5-4 (a)）， SSP-MMC 的表现比所有基线都好，这并不令人惊讶。THR 与 SSP-MMC 的优化目标一致，SSP-MMC可以达到这个指标的上限。为了量化每种算法性能之间的相对差异，实验比较了 THR=1000 的天数（图中标记为 ★）：SSP-MMC 为 202 天， THRESHOLD 为 238 天，Memorize 为 332 天，而其余算法在模拟结束前都没有达到这一标准。与 THRESHOLD 相比，SSP-MMC 节省了 15.12% 的复习时间。

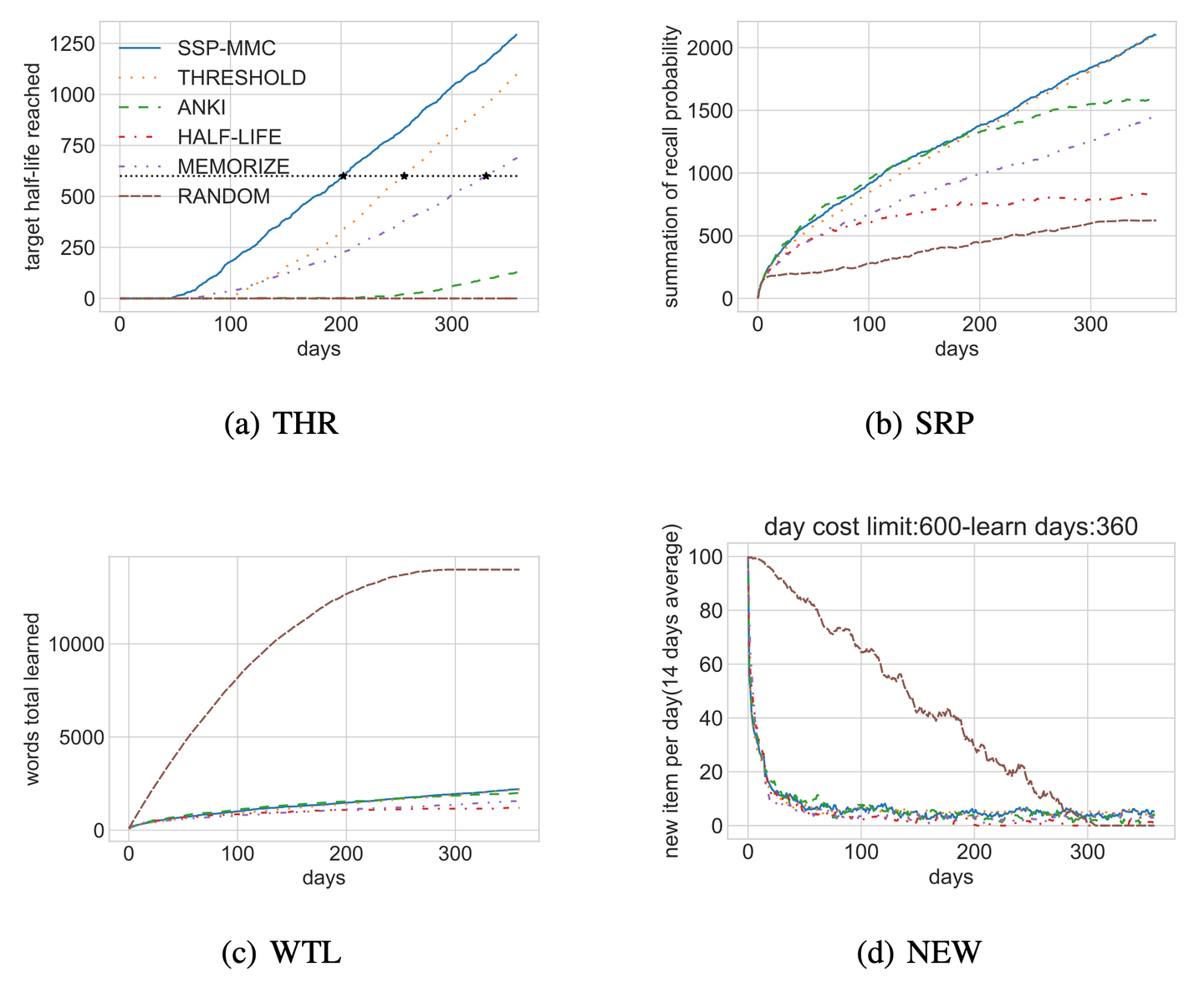
在指标 SRP 上（图 5-4 (b)）的结果与 THR 上的结果相似。这意味着学习者按照 SSP-MMC 的时间表学习会记得最多。在指标 WTL 上（图5-4 (c)），RANDOM 优于其余算法，因为只要调度算法不安排复习，学习者就可以继续学习新的单词，但这是以忘记已经学过的单词为代价的。此外，SSP-MMC 胜过其他基线，因为它将记忆的成本降到最低，给学习者更多的时间来学习新单词。

5.5 研究结果总结与限制

本项工作的目的有三个：第一，在前人的基础上，改进记忆预测模型，降低长期记忆预测误差。第二，提出间隔重复调度算法的优化目标，并构建算法计算最优策略。第三，将记忆预测模型和间隔重复调度算法整合至一个系统。

本文研究了使用不同时序特征时预测误差的变化，并对损失函数进行了调整。本文发现只要引入时序特征，就能显著降低长期记忆的预测误差。同时，使用绝对百分比误差的效果要优于绝对误差和均方误差。此外，通过提高 LSTM 隐藏层节点数量可以降低预测误差，但效果有限。在间隔重复调度问题上，这项工作的主要目标是在相同复习期限和每日学习成本约束下对比不同算法的

长期记忆达成量和记住的材料期望数量。本文进行了模拟实验，使用最小化复习成本来训练本文的复习调度算法，然后在达到目标半衰期的记忆数量 THR、累计记忆期望 SRP 和累计新增的记忆数量 WTL 三个指标上评估算法表现。本文观察到，在 THR 和 SRP 两个指标上，SSP-MMC 得到的最优策略超越了所有对比基线，这也是本文预期的，而 WTL 指标存在漏洞。而由于项目时间限制，本文仅将 SSP-MMC 算法部署至墨墨背单词的复习策略优化模块，预测模块则采用统计数据和插值拟合的方式实现。

本项工作的限制主要有以下三点：

实验数据仅来自墨墨背单词，可能在语言学习以外的科目上表现不佳。
在聚合数据的过程中，忽略了学生记忆能力的差异，因为本文预计这将会进一步加重数据稀疏的问题。这种忽略可能会导致最终的复习调度算法只对平均水平的学生而言是最优的。
在选择状态空间维数时，由于 SSP-MMC 的算法复杂度随着维数指数增加，为了在合理的时间内计算出最优策略，本文以牺牲预测精度为代价，仅在 LSTM-HLR 中应用了 4 个隐藏层节点。这种牺牲可能导致最优策略于实际的情况有一定的偏差。

5.6 可持续性和伦理道德

这项工作基本上不会对社会构成任何重大的可持续性或伦理道德问题。从可持续角度来看，唯一的问题是训练 LSTM-HLR 和 SSP-MMC 的计算时间很长，从而消耗更多的能量。从伦理角度来看，一个问题是用于训练 LSTM-HLR 和 SSP-MMC 的数据应足够普适，以免受到任何形式的偏见影响。与任何数据驱动的系统一样，应始终牢记数据隐私问题。当这些系统部署在生产环境中，学生在学习过程的隐私就变得非常重要，保护学生隐私有助于防止学生因记忆知识需要更长时间而被嘲笑的欺凌问题。学生在复习中的表现也会影响他们的积极性和自尊心，因此在设计为学生服务的间隔重复系统时必须考虑这些因素。在这项工作中，本文对数据进行了脱敏处理，尽可能地避免学生隐私的泄露。

另一个主要的伦理问题可能是人工智能接管了真人教学。但是，这种情况发生的可能性需要很长时间。这对下一代人记忆知识可能有很大的帮助，但要达到这一境界，还需要付出很大的努力。例如，真人教师在进行复习测试时也可以考虑其他因素，例如面部表情、语调等，以确定学生是否确定自己的答案。实现类似的目标意味着使用单独的人工智能系统来表达面部表情、语音等。阅读或使用一个非常复杂的系统，将所有这些任务一起完成以做出决策。人类教师还采取措施确保学生不会在考试中作弊。从另一角度来看，真人教师有时会对某些学生表现出偏见，而目前的复习调度算法可以避免这一问题。

5.7 本章小结

本章中，本文在记忆预测和复习规划两个方面对比已有的算法，其中还涉及了结合 LSTM-HLR 和 SSP-MMC 时考虑的状态空间维数问题。

在长期记忆预测上，LSTM-HLR 算法的误差低于目前最先进的算法。并在消融实验中，本文发现在仅使用反馈序列特征也优于 HLR 模型。间隔序列特征和回忆概率序列特征都对模型的预测有正面贡献，其中回忆概率序列特征的贡献更大。并且间隔序列特征和回忆概率序列特征的贡献分别起作用的，当结合两个特征使用时，结果优于单独仅用其中一个特征。在状态空间维数选择的过程中，本文发现随着隐藏层节点数量的增加，预测误差的下降较为缓慢，而状态空间的复杂度呈指数增加。在复习规划上，SSP-MMC 在由 LSTM-HLR 构建的间隔重复模拟环境中与其余算法相比，最小化了学习者的记忆成本。

本项工作的研究结果确定了时序特征在长期记忆预测中的重要作用，同时证明了绝对百分比误差在预测记忆半衰期时是一个较好的损失函数。在复习规划问题中，研究结果反映了以最小化记忆成本为优化目标，能够达到最大化记忆期望的结果。本项工作的限制主要集中在数据范围有限上，没有区分不同学习者的差异，以及在其他学科上的有效性。此外，SSP-MMC 算法的复杂度也限制其性能进一步提升。在可持续性和伦理道德上，本项工作基本上没有问题。不如说，通过自动化复习安排，节约人类教师的精力用于更重要的地方正是本项工作的价值之一。

LSTM-HLR 模型在预测记忆方面有了较大的提升，但尚未考虑学习者自身因素对长期记忆的影响，考虑学习者特征对此记忆状态转移的影响是一个很有吸引力的方向。此外，在语言学习以外的场景进行相似的工作也是值得的，可以验证本工作所提出的方法的普适性。最后，学习者使用间隔重复方法的场景十分多样化，根据学习者的目标来调整 SSP-MMC 算法的优化目标也是一个值得研究的问题。简言之，在未来工作上，探究学习者内部差异和探索更多的学习科目、更个性化的复习目标都是具有诱惑力的工作方向。

结论

本文建立了第一个包含时序信息的记忆行为数据集，进行了长期记忆的回忆概率及记忆半衰期预测实验和复习调度的记忆成本约束模拟实验。通过实验，得到了长期记忆预测模型的横向对比数据和消融实验数据，以及模拟间隔重复调度的学习数据。数据分析表明，相较于 HLR 模型，考虑时序信息的 LSTM-HLR 模型在拟合用户长期记忆上的精度有显著提升，基于随机动态规划的间隔重复调度算法 SSP-MMC，在各项指标上都超过了之前的算法。根据分析结果，我们验证了在长期记忆模型中，时序特征对预测记忆半衰期十分有效的假设。这表明基于循环神经网络和随机最优控制理论的间隔重复调度算法能够有效地预测学习者的长期记忆状态和提高学习者的记忆效率。最终，我们达成了本项工作的目标，构建一套完整的间隔重复系统，提高学习者的记忆效率。本文的主要创新之处归纳为以下两点:

通过提取记忆行为序列特征，提出了一种新的基于 LSTM 循环神经网络的长期记忆预测模型，通过大量实验，验证了时序特征的重要性，使用 3 通道时序特征的 LSTM-HLR 模型对回忆概率预测的误差低至 1.47%，相较于 HLR 模型的 8.28%，有所改进;
通过应用 LSTM-HLR 模型模拟学习者在间隔重复过程中的长期记忆动态，搭建了一种新的间隔重复模拟环境，并引入随机最优控制的相关方法，提出了一种以最小化学习者记忆成本的间隔重复调度算法，通过模拟实验，验证了优化目标的合理性，基于随机动态规划的 SSP-MMC 调度算法相比基于阈值的方法节省了 15.12% 的复习时间。

总体而言，本文就基于 LSTM 和间隔重复模型的复习调度算法做出来较为完整的探索和研究。但是，如何充分利用记忆行为数据、更丰富的特征和指标、更广泛的学科材料以及更通用的系统架构，为不同学习者在通用的学习平台和科目中提供高效且稳定的间隔重复规划服务，仍然存在很多问题，这需要研究人员的探索。随着在线教育的普及，更多不同的学习者行为信息源也在增加，未来间隔重复调度算法研究仍然具有艰巨的研究挑战和广阔的应用前景。

该毕设的部分研究成果已发表在中文核心期刊《中文信息学报》发表^[4]；另有一篇论文“A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling”已被 2022 ACM SIGKDD 接受^[5]。

参考文献

[1] REISBERG D. Cognition: Exploring the Science of the Mind[M]. Seventh edition ed. New York: W. W. Norton & Company, 2019.

[2] EBBINGHAUS H. Memory: A Contribution to Experimental Psychology[M]. RUGER H A, BUSSENIUS C E. New York: Teachers College Press, 1913.

[3] KRAMÁR E A, BABAYAN A H, GAVIN C F, et al. Synaptic Evidence for the Efficacy of Spaced Learning[J]. Proceedings of the National Academy of Sciences, 2012, 109(13): 5121-5126.

[4] CEPEDA N J, PASHLER H, VUL E, et al. Distributed Practice in Verbal Recall Tasks: A Review and Quantitative Synthesis[J]. Psychological Bulletin, 2006, 132 (3): 354-380.

[5] SMOLEN P, ZHANG Y, BYRNE J H. The Right Time to Learn: Mechanisms and Optimization of Spaced Learning[J]. Nature Reviews. Neuroscience, 2016, 17(2): 77-88.

[6] CEPEDA N J, VUL E, ROHRER D, et al. Spacing Effects in Learning: A Temporal Ridgeline of Optimal Retention[J]. Psychological Science, 2008, 19(11): 1095-1102.

[7] DELANEY P F, VERKOEIJEN P P J L, SPIRGEL A S. Spacing and Testing Effects: A Deeply Critical, Lengthy, and At Times Discursive Review of the Literature[J]. Psychology of Learning and Motivation, 2010, 53: 63-147.

[8] BAHRICK H P, PHELPHS E. Retention of Spanish Vocabulary over 8 Years[J]. Journal of Experimental Psychology: Learning, Memory, and Cognition, 1987, 13 (2): 344-349.

[9] TJ S, LIM P, SE P, et al. Impact of Online Education on Intern Behaviour around Joint Commission National Patient Safety Goals: A Randomised Trial[J]. BMJ quality & safety, 2012, 21(10): 819-825.

[10] MAASS J K, PAVLIK P I, HUA H. How Spacing and Variable Retrieval Practice Affect the Learning of Statistics Concepts[C]//Artificial Intelligence in Education. Cham: Springer International Publishing, 2015: 247-256.

[11] CARPENTER S K, PASHLER H, CEPEDA N J. Using Tests to Enhance 8th Grade Students’ Retention of U.S. history facts[J]. Applied Cognitive Psychology, 2009, 23(6): 760-771.

[12] SETTLES B, MEEDER B. A Trainable Spaced Repetition Model for Language Learning[C]//Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics. Berlin, Germany: Association for Computational Linguistics, 2016: 1848-1858.

[13] ZAIDI A, CAINES A, MOORE R, et al. Adaptive Forgetting Curves for Spaced Repetition Language Learning[C]//Lecture Notes in Computer Science: Artificial Intelligence in Education. Cham: Springer International Publishing, 2020: 358-363.

[14] REDDY S, LEVINE S, DRAGAN A. Accelerating Human Learning with Deep Reinforcement Learning[C]//NIPS’17: Workshop: Teaching Machines, Robots, and Humans. 2017: 9.

[15] WIXTED J T, CARPENTER S K. The Wickelgren Power Law and the Ebbinghaus Savings Function[J]. Psychological Science, 2007, 18(2): 133-134.

[16] MOZER M C, LINDSEY R V. Predicting and Improving Memory Retention: Psychological Theory Matters in the Big Data Era[J]. Big Data in Cognitive Science, 2016, 34.

[17] PAVLIK P I, ANDERSON J R. Using a Model to Compute the Optimal Schedule of Practice[J]. Journal of Experimental Psychology: Applied, 2008, 14(2): 101-117.

[18] ANDERSON J R, BOTHELL D, BYRNE M D, et al. An Integrated Theory of the Mind[J]. Psychological Review, 2004, 111(4): 1036-1060.

[19] MOZER M C, PASHLER H, CEPEDA N, et al. Predicting the Optimal Spacing of Study: A Multiscale Context Model of Memory[C]//NIPS’09: Proceedings of the 22nd International Conference on Neural Information Processing Systems. Red Hook, NY, USA: Curran Associates Inc., 2009: 1321–1329.

[20] PIMSLEUR P. A Memory Schedule[J]. The Modern Language Journal, 1967, 51 (2): 73-75.

[21] LEITNER S. So lernt man leben[M]. 1. - 10. tsd ed. München, Zürich: Droemer-Knaur, 1974.

[22] WOZNIAK P A, GORZELANCZYK E J. Optimization of Repetition Spacing in the Practice of Learning[J]. Acta Neurobiologiae Experimentalis, 1994, 54(2): 59-62.

[23] TABIBIAN B, UPADHYAY U, DE A, et al. Enhancing Human Learning via Spaced Repetition Optimization[C]//Proceedings of the National Academy of Sciences. National Academy of Sciences, 2019: 3988-3993.

[24] UPADHYAY U, DE A, GOMEZ-RODRIZUEZ M. Deep Reinforcement Learning of Marked Temporal Point Processes[C]//NIPS’18: Proceedings of the 32nd International Conference on Neural Information Processing Systems. Red Hook, NY, USA: Curran Associates Inc., 2018: 3172–3182.

[25] SINHA S. Using Deep Reinforcement Learning for Personalizing Review Sessions on E-Learning Platforms with Spaced Repetition: 2019:217[D]. KTH, School of Electrical Engineering and Computer Science (EECS), 2019: 82.

[26] YANG Z, SHEN J, LIU Y, et al. TADS: Learning Time-Aware Scheduling Policy with Dyna-Style Planning for Spaced Repetition[C]//Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. New York, NY, USA: Association for Computing Machinery, 2020: 1917-1920.

[27] HOCHREITER S, SCHMIDHUBER J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1735-1780.

[28] CHO K, van Merrienboer B, BAHDANAU D, et al. On the Properties of Neural Machine Translation: Encoder-Decoder Approaches[A]. 2014. arXiv: 1409.1259. [29]BERTSEKAS D P. Reinforcement Learning and Optimal Control[M]. 2nd printing (includes editorial revisions) ed. Belmont, Massachusetts: Athena Scientific, 2019.

[30] REDDY S, LABUTOV I, BANERJEE S, et al. Unbounded Human Learning: Optimal Scheduling for Spaced Repetition[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, NY, USA: Association for Computing Machinery, 2016: 1815-1824.

[31] HUNZIKER A, CHEN Y, AODHA O M, et al. Teaching Multiple Concepts to a Forgetful Learner[C]//NIPS’19: Proceedings of the 33rd International Conference on Neural Information Processing Systems. Red Hook, NY, USA: Curran Associates Inc., 2019: 4048–4058.

[32] DIETTERICH T G. Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms[J]. Neural Computation, 1998, 10(7): 1895-1923.

[33] BJORK R A, BJORK E L, et al. A New Theory of Disuse and an Old Theory of Stimulus Fluctuation[J]. From learning processes to cognitive processes: Essays in honor of William K. Estes, 1992, 2: 35-67.

[34] MADDOX G B, BALOTA D A, COANE J H, et al. The Role of Forgetting Rate in Producing a Benefit of Expanded over Equal Spaced Retrieval in Young and Older Adults[J]. Psychology and Aging, 2011, 26(3): 661-670.

致谢

衷心感谢导师苏敬勇教授对本人的精心指导。他的言传身教将使我终生受益。

感谢 @墨墨背单词的同事们，他们开发、维护、运营的墨墨背单词 APP 是让本人工作得以进行的基础。

感谢 Piotr Wozniak^[6] 和 Andy Matuschak，他们在记忆算法和间隔重复工具上的热诚与贡献，让我下定决心走上记忆研究之路。

感谢 @Thoughts Memo 汉化组的朋友们，在本人写作期间提供了很多心理上的支持。

感谢 @知乎上的答主们，本人的许多知识是从他们的文章与回答中学到的。

感谢哈工大 LATEX 论文模板 HITHESIS^[7]，帮本人节省了许多调整格式的宝贵时间！

我是如何在本科期间发表顶会论文的？（内含开源代码和数据集）KDD'22 | 墨墨背单词：基于时序模型与最优控制的记忆算法 [AI+教育]间隔重复记忆算法：e 天内，从入门到入土。间隔重复记忆算法研究资源汇总 open-spaced-repetition/fsrs4anki: A modern Anki custom scheduling based on free spaced repetition scheduler algorithm (github.com)

参考

1. Optimizing Spaced Repetition Schedule by Capturing the Dynamics of Memory https://ieeexplore.ieee.org/document/10059206
2. 为了缩小搜索空间，将其设置为[1,h]
3. 为了简化问题，只考虑 r
4. 基于LSTM的语言学习长期记忆预测模型 http://jcip.cipsc.org.cn/CN/Y2022/V36/I12/133
5. A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling https://www.maimemo.com/paper/
6. 彼得 · 沃兹尼亚克 ./303204832.html
7. 嗨！thesis！哈尔滨工业大学毕业论文LaTeX模板 https://github.com/hithesis/hithesis

专栏：学委叶哥的随笔

← 返回目录

摘要

第 1 章 绪论