有没有什么方法能够提高工作记忆容量的？常见的一些联想、定桩等方法似乎没有办法从根本上提高工作记忆容量。

问题描述

这里有对工作记忆的定义：http://baike.baidu.com/view/1009037.htm

说说我对联想和定桩的看法：
1. 记忆的本质是联想，所以联想只是更符合大脑的思维方式，更多体现的是一种技巧。
2. 定桩则是将新的知识与已有的知识建立联系，自然也符合大脑认知方式，所以我觉得也只是一种技巧。
3. 虽然说熟能生巧，但是如果是一个毫无接触过的领域，之前记忆扑克、数字（圆周率)是否有用？我觉得吧，要看模式，模式是否相关。看过一个例子，说国际象棋大师如果去记忆一些毫无关联的棋子，并不能比初学者记忆的更快更牢，速度反而可能会变慢。

从人脑硬件层面来说，没有办法。人脑的工作记忆数量大概就是 7 +- 2 个组块，而每个组块的也就几个 bits（但这个可以通过提高刺激的维度来增加）。

但从软件上，我们有提高工作记忆容量的方法，那就是对组块进行重新编码，将复杂的模式存入长期记忆，在思考的时候调用这些模式来处理复杂的信息。

以下内容摘自 Andy Matuschak 的笔记，由 @Thoughts Memo 汉化组翻译。

人类作为信息处理机时的“信道容量”

要探究一个人信息处理能力的极限，一个方式是询问他能从观察到的刺激中，重现出多少信息。在这个框架下，我们可以利用信息论提供的工具，将观察者作为一个通讯信道来建模。 zhèi 个示意图 (Pollack, 1953, p. 422) 描绘了这个模型：

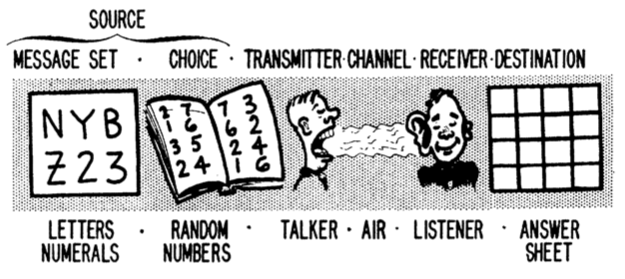
理想的信道可以重现你给定的任何输入。而实际的信道，多数（包括人类）的复现会掺杂错误，并且随着输入中的信息增多而增多。这个行为通常是渐进发生的：一个信道会完美地传输它的输入，直到超过了一定的阈值。过了这个阈值 —— 即我们所称为 {信道容量（channel capacity）} ——，输入输出的相关性随之下降，而传输的总 bit 数保持不变

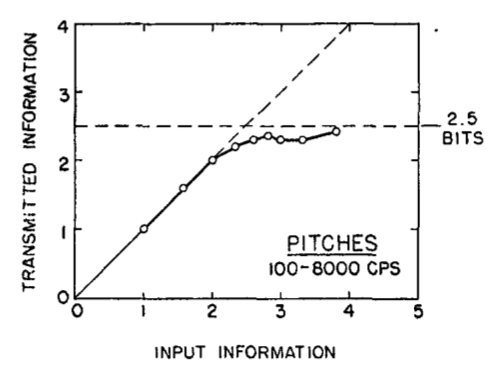
对人类绝对判断广度^[1]的实验可以用来建模人类的信道模型。Miller （1956）回顾了历史经验数据，认为对于无维度的刺激，人类的信道容量大约为 {2.6} bits

例如这里 Miller 给出的一张图 (1956, p. 83), 使用了 Pollack (1952, 1953) 关于人类对音高绝对判断的实验数据，并用信息论的方法进行了重构。

问：如果你知道一个受试者的绝对判断广度（对于单项、单维量级），你如何获得他们的信道容量？
答：通道容量= $\log_2(\textrm{绝对判断广度})$

问：为什么绝对判断广度与人的信道容量有 $\log_2$ 的关系？
答：信道容量以比特表示。如果绝对判断广度是 8 个类别，你需要 $\log_2(8)$ bits 来表示每个状态。

参考文献

Miller, G. A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 63(2), 81–97. https://doi.org/10.1037/h0043158 Miller - The magical number seven, plus or minus two

Pollack, I. (1952). The Information of Elementary Auditory Displays. The Journal of the Acoustical Society of America, 24(6), 745–749. https://doi.org/10.1121/1.1906969

Pollack, I. (1953). Assimilation of Sequentially Encoded Information. The American Journal of Psychology, 66(3), 421–435. JSTOR. https://doi.org/10.2307/1418237

链接至本文（已汉化）

声明

Thoughts Memo 汉化组译制
原文：Channel capacity of humans as information processors (andymatuschak.org)

绝对判断广度

人们难以准确识别单维刺激物的绝对数量。例如，假设我在只有 0 和 100 标签的数线上标记一个点。然后我让你估计这个标记点对应的数字。你的答案与真实位置相差多少？

换一种说法，你能可靠地区分多少个类别？如果我可以选择 0-100 中的任何一个数字，你可能不会预计得那么准确，但如果我只能选择 20、40、60 和 80，你的答案可能会完全相关。我们可以慢慢增加可能的选择数量，找到人们不能可靠地区分任何额外类别的界限。我们还可以对其他刺激重复同样的实验，比如声音的响度或音调，或者盐水的浓度，或者颜色的色调。

{ Miller }（1956 年）称这个阈值为绝对判断广度，他的文献回顾表明，这个阈值在{ 七 }左右，在不同的刺激类型中变化很小，令人惊讶。

这个数量很重要，因为它代表了人类信息处理的基本限制：人类作为信息处理机时的“信道容量”^[2]

问：Miller 的绝对判断广度描述了哪些类型的刺激？
答：一维量级

问：绝对判断广度变化的大致数量级是什么？
答：10^0

问：为说明某人对某刺激的绝对判断广度，可以做什么实验，举个例子。
答：为盐水的浓度、形状的大小、线条的倾斜度等分配数字

问：人类只能可靠地将一个刺激（如盐水浓度）区分为大约 7 个不同的单维量级。Miller（1956）把这个极限称为什么？
问：绝对判断广度

参考文献

Miller , G. A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 63(2), 81–97. https://doi.org/10.1037/h0043158 Miller - The magical number seven, plus or minus two

链接至本文（已汉化）

声明

Thoughts Memo 汉化组译制
原文：Span of absolute judgment (andymatuschak.org)

人类认知中的「组块」

在考虑人类的信息处理能力时，工作记忆容量一般与项目复杂性无关^[3]，因此我们必须区分正在处理的记忆内容的数量（一个“块”，由工作记忆大小限制）和每块记忆内容的复杂性（各自受绝对判断广度^[4]限制）。

米勒写道（1956 年，第 92 页）：

我已经习惯了区分比特信息和组块信息。那么我可以说，对于绝对判断来说，信息的比特数是恒定的，而对于瞬时记忆来说，信息的组块数是恒定的。

重要的是：人类信道容量随着每组块比特的增加而增加^[5]和重新编码可以增加组块的大小^[6]。

特别是在更复杂的重新编码方案中，组块可以表示相当抽象的属性：例如，音乐家在即兴创作时考虑「张力」，或者国际象棋选手考虑「力量线」。

参考文献

Miller, G. A. (1956). 神奇的数字 7 ± 2：我们处理信息能力的一些限制。Psychological Review, 63(2), 81-97. https://doi.org/10.1037/h0043158 Miller - The magical number seven, plus or minus two

链接至本文（已汉化）

声明

Thoughts Memo 汉化组译制
原文：“Chunks” in human cognition

重新编码可以提升组块大小

人类的信道容量随着每个组块的比特量的增加而增加^[7]。但我们不需要依赖对人脑刺激的「内在」组块大小。我们可以通过重新编码来增加刺激的有效组块大小——也就是说，精神上重组刺激的信息，得到组块描述更宏观的模式。这些块状模式也被称为心理表征，取自 Ericsson 和 Pool.

例如，为记忆一串二进制数字，可以将其三位一组转换成八进制来记忆（例如，010=2，101=5，诸如此类），这样记忆容量大约能增加两倍（Miller, 1956）。Chase 和 Ericsson(1982) 使用这类技术将一个学生的数字广度提高到 80 位，具体做法是将数字重新分层编码为 4 位十进制的组块。

重新编码很重要，因为它不仅能帮助我们记住有用的信息，而且可能是处理各种复杂材料的关键步骤（具体而言，专业水准需要建立复杂的组块重新编码方案^[8]）。钢琴演奏者最初按单个音符阅读乐谱（C、E、G——啊，是 C 和弦！），但后来能将看到弦音符的整体形状而识别为一个和弦（啊，一个 C 大调三和弦）。单个单个读音符是不可能视奏颇有难度的音乐的。

这些模式（例如大三和弦的形状）一旦被储存在长期记忆中，就能作为「组块」使用。

Chase and Simon - Perception in chess 记录的实验数据表明，国际象棋大师的组块更大（可能还有层级组块机制）。

相关笔记：复杂的概念可能很难学习，部分原因是工作记忆容纳不下其组分^[9]

参考文献

Chase, W. G., & Ericsson, K. A. (1982). Skill and Working Memory. In G. H. Bower (Ed.), Psychology of Learning and Motivation (Vol. 16, pp. 1–58). Academic Press. https://doi.org/10.1016/S0079-7421(08)60546-0

链接至本文（已汉化）

声明

Thoughts Memo 汉化组译制
原文：Recoding can increase chunk size (andymatuschak.org)

参考

1. 绝对判断广度 ./535214087.html
2. 人类作为信息处理机时的“信道容量” ./461578699.html
3. 工作记忆容量一般与项目复杂性无关 ./465252781.html
4. 绝对判断广度 ./535214087.html
5. 人类的信道容量随着每个组块的比特量的增加而增加 ./462011439.html
6. 重新编码可以提升组块大小 ./432809617.html
7. 人类的信道容量随着每个组块的比特量的增加而增加 ./462011439.html
8. 专业需要建立复杂精细的组块重编码架构 ./467156331.html
9. 复杂的概念可能很难学习，部分原因是工作记忆容纳不下其组分 ./400919428.html

← 返回目录