创造力、乐趣与内在动机的形式化理论
作者:于尔根·施密德胡伯(Jürgen Schmidhuber)
自 1990 年以来,施密德胡伯(JS)一直在构建充满好奇心和创造力的智能体。它们可被视为简单的人工科学家和艺术家,怀有一种通过不断设计新实验来探索世界的内在渴望。这些智能体永不停止地生成新颖、惊奇的事物,其核心由两个学习模块构成:(A) 一个自适应的预测器或压缩器,用于对智能体与环境互动过程中不断增长的数据历史进行建模;以及 (B) 一个通用的强化学习器 (RL),负责选择能塑造这段历史的行动。模块 (A) 的**「学习进度」可以被精确测量,而这正是该智能体的「乐趣」所在,即模块 (B) 的内在奖励**。换言之,(B) 的动机,就是去学习如何创造出那些 (A) 尚不知晓但又能轻松学会的**「有趣」事物。为了最大化未来的预期奖励,在没有食物等外部奖励的情况下,(B)** 会学习越来越复杂的行为,这些行为能产生最初令人惊奇(但最终会变得无聊)的新颖模式,从而使 (A) 的模型迅速改进。自 1990 年以来的众多相关论文可见此链接——其中的关键论文包括 1991、1995、1997(2002)、2006、2007、2011 年的成果(亦可参见本页底部)。这些智能体体现了一个简洁而普适的、关于乐趣与创造力的形式化理论,它解释了人类及非人类智能的诸多核心侧面,包括选择性注意力、科学、艺术、音乐和幽默(详见下文)。
更形式化的表述: 设 O(t) 为某个主观观察者 O 在时间 t 的状态。设 H(t) 为其截至时间 t 的历史行为、感知和奖励。O 拥有一种自适应的方法来压缩 H(t) 或其部分。我们将任何数据 D 对于观察者 O(t) 的主观瞬时简洁性/可压缩性/规律性/美感 B(D,O(t)) 定义为:在给定观察者当前有限的先验知识和压缩能力下,编码 D 所需比特数的负值(注意:这不同于其「有趣性」或审美价值,见下文)。我们进而将数据 D 对于观察者 O 在离散时间步 t>0 的主观**「有趣性」/「新颖性」/「惊奇感」/「审美奖励」/「内在愉悦」/「乐趣」** I(D,O(t)) 定义为:I(D,O(t)) = B(D,O(t)) - B(D,O(t-1)),即主观简洁性或美感的变化量或一阶导数。随着学习智能体不断改进其压缩算法,原先看似随机的数据会变得在主观上更有规律、更「美」,编码所需的比特数也随之减少。只要这个学习过程尚未完成,数据就保持其「有趣性」;但最终,即便它很「美」,也会变得无聊。在时间 t,设 ri(t) = I(H(t),O(t)) 为因发现历史数据 H(t) 中的新颖模式而带来的压缩进度提升,我们称之为瞬时乐趣或内在奖励。设 re(t) 为当前的外部奖励(如果有的话),则总奖励 r(t) = g(ri(t), re(t)),其中 g 是一个权衡内外奖励的函数(例如 g(a,b) = a+b)。智能体在时间 t0 的目标是最大化 E[∑Tt=t0r(t)],其中 E 是期望算子,T 是生命终点。这一目标可通过我们的强化学习算法之一来实现。
实现方案: 该理论已通过以下几种变体得以实现。[1991a]: 基于自适应循环神经网络作为预测世界模型的非传统强化学习(无马尔可夫假设限制),通过最大化以内在奖励(由预测误差衡量)来驱动。[1991b]: 传统强化学习,最大化由预测误差的改进量所衡量的内在奖励。[1995]: 传统强化学习,最大化由智能体先验与后验概率分布之间的相对熵所衡量的内在奖励。[1997-2002]: 通过两个玩家相互对赌的零和内在奖励游戏来学习概率性的、层级化的程序和技能。每个玩家都试图通过设计算法实验来「智胜」或「惊吓」对方,即找到双方预测结果不一致的实验,同时将学习的计算成本也纳入考量,从而学习何时学、学什么。1991-2002 年的论文也通过实验证明,内在奖励能显著加速有目标的学习和外部奖励的获取。JS 还在数学上描述了由预测进度或压缩进度驱动的最优(及更优)的、内在驱动型系统 [2006-]。所有相关论文列表见此。
发展机器人学: 我们的持续学习的人工智能体经历了类似生命的发展阶段:某个有趣的事物会吸引它一段时间,但一旦它无法再改进其预测,便会感到无聊;然后,它会尝试为自己创造新的任务,在已有知识的基础上学习更新颖、更复杂的技能;接着,这也会变得无聊……如此循环,构成一个开放式的学习过程。
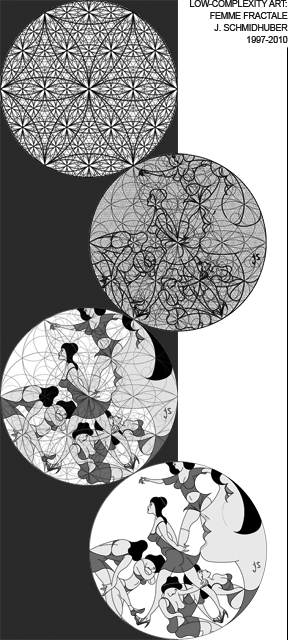
该理论如何解释艺术: 艺术家(及艺术欣赏者)因创造(及欣赏)新颖的模式而获得奖励。所谓新颖的模式,是指那些既非全然任意(如不可压缩的随机白噪声),也非以完全已知的方式规则,而是以一种相对于观察者当前知识而言全新、但又可被学习的方式呈现出的规律(即学习后,编码该数据所需的计算资源更少)。尽管该形式化理论能解释创造或欣赏所有类型艺术的欲望,但低复杂度艺术(1997)以一种尤为清晰的方式阐释了它。**右图示例:**许多观赏者表示,在主动审视这幅自相似的《分形女性》时,他们从发现那些简洁而新颖的模式中获得了愉悦。观赏者的学习过程降低了数据的主观复杂性,从而产生了暂时的、主观美感的一阶导数高值,即一条陡峭的学习曲线。同样,这位借助计算机的艺术家也因找到一种满意的方式,用分形圆创作出这件低复杂度艺术品而获得了奖励,尽管这花费了他漫长的时间和数千次令人沮丧的尝试。这件作品的低算法复杂度可解释如下:画框是一个圆,其最左点是另一个同尺寸圆的圆心。任何两个同尺寸圆的相切或相交处,都是另外两个圆的圆心,其尺寸分别为相等和一半。画中的每一笔都是某个圆的弧段,其端点是圆的相切或相交处。画中有少数大圆和大量小圆。这使得该图像能被一个极短的程序高效地编码。也就是说,《分形女性》具有极低的算法信息或柯尔莫哥洛夫复杂性。点击图片可放大。(《分形女性》这一名称创于 1997 年。2012 年,该作品在科学频道的《与摩根·弗里曼一起穿越虫洞》节目中首次亮相电视。)
该理论如何解释音乐: 为何有些乐曲比其他乐曲更有趣、更富美感?绝不是那首你刚听了五十遍的曲子,它已变得过于可预测。也绝不是那首节奏音调完全陌生的怪曲,它听起来太不规律,充满了主观噪音。真正吸引人的旋律,是那些既足够陌生,包含意想不到的和声或节拍,又足够熟悉,能让你迅速识别出其中存在一种可被学习的新规律——一个新颖的模式!当然,它最终也会变得无聊,但不是现在。这一切都完美契合该理论:观察者的压缩器试图压缩其听觉历史,而行动选择器(作曲家)则试图创造出能让压缩器性能提升的声音序列。那些有趣、富含美感的乐曲,正是包含了未知但可学习的规律的片段,因为它们能带来压缩上的进步。而无聊的模式,要么是已知的,要么是随机的,要么是结构过于复杂难以理解的。
该理论如何解释幽默: 思考这句话:「生物的驱动力来自『四大 F』:Feeding(进食)、Fighting(战斗)、Fleeing(逃跑)、Mating(交配)。」 许多初次读到的人会觉得好笑。为什么?当眼睛扫描文本时,大脑接收到一串可被部分压缩的视觉输入流(因为你认识字母和单词)。但最后一个词打破了读者对另一个「F」开头的词的预期。这种预期失败最初会导致压缩效率降低(偏离预测需要额外比特来编码)。然而,压缩器很快就会启动学习算法,通过发现这个「包袱」与前文及背景知识之间的非任意、可压缩的联系(即新模式),来提升其压缩性能。这个过程节省了几个比特的存储空间,而节省的比特数(或类似的学习进度度量)就成了观察者的内在奖励,即「乐趣」。虽然以往的幽默理论也强调「惊奇」,但它们缺乏一个核心概念:通过学习带来的压缩「进度」所衡量的新颖模式检测。当意外只是随机噪音时,压缩进度为零,自然也毫无乐趣可言。该幽默理论的应用可见于此视频。
该理论如何解释科学: 如果宇宙的历史是可计算的(目前尚无证据反驳此可能性),那么其最简洁的解释便是能计算出它的那个最短程序。不幸的是,我们没有通用的方法找到这个最短程序。因此,物理学家们传统上采用增量的方式,每次只分析世界的一个小侧面,试图找到比以往任何定律都更能描述其观察的简单规律——这本质上是在寻找一个能更好地压缩观测数据的程序。一次异常巨大的压缩突破,便堪称一次**「发现」**。例如,牛顿的引力定律可以被表述为一小段代码,它极大地压缩了无数关于落体运动的观测序列。尽管其预测力有限,但它通过为高概率事件分配短编码,大大减少了编码数据流所需的比特数。爱因斯坦的广义相对论则带来了进一步的压缩,因为它简洁地解释了许多牛顿定律无法预测的偏差。大多数物理学家相信,前方仍有提升空间,而这正是驱动他们不断研究的动力。当不为外部奖励所动时,物理学家们只是在追随他们对「压缩进度」的内在渴望!
该理论如何解释学习运动技能的乐趣:抖机灵带来的笑声,与婴幼儿及成人掌握新技能时的喜悦,在很多方面是相似的。JS 在 25 岁后学会了抛接三个球。这个过程是渐进且充满回报的:从一秒、两秒到最终能熟练掌握。他从镜中看到,每当取得进步时,自己脸上都会浮现出一种傻傻的笑容。后来,他的小女儿在第一次能独立站稳时,也露出了同样的笑容。这一切都完美契合该理论:这种笑容由内在奖励触发,源于生成了一段包含前所未有的新颖模式的数据流——例如,观察自己抛球的感官输入序列,与更熟悉的观察他人抛球的体验截然不同,因此是真正新颖且具有内在回报的,直到你的压缩器(例如一个循环神经网络)对此习以为常。**图示:**iCub 婴儿机器人,用于 JS 的欧盟项目 IM-CLEVER,该项目旨在机器人上实现乐趣与创造力理论。(不过,至今 iCub 仍无法连续抛接三球超过 60 秒——任重道远。)
该理论如何推广到「主动学习」: 传统的主动学习(Active Learning)旨在以最小的数据评估成本来优化一个函数,通常局限于监督分类任务。而创造力理论的框架更为通用,它额外考虑了:(1) 强化学习智能体,其行动与信息增益之间可能存在任意延迟;(2) 获取数据序列(而非单个数据点)时,高度依赖环境的成本;(3) 行动与感知序列中任意的算法或统计依赖性;(4) 学习新技能的计算成本。与以往方法不同,这些系统测量并最大化由智能体自创的、通用的时空模式中的算法新颖性(即可学习但未知的可压缩性)。
预期与意外之间不存在客观的「理想比例」: 以往一些信息论视角下的美学理论,试图寻找审美对象中「秩序」与「复杂性」之间的某种客观「理想比例」。而 JS 的方法无需此假设。相反,他的趣味性度量反映的是编码一个对象所需比特数的变化量,并明确考虑了观察者主观的先验知识及其有限的压缩改进能力。因此,审美体验的价值并非由客体本身定义,而是由主观的、学习中的观察者所取得的算法压缩进度所定义。
总结: 要构建一个有创造力的系统,我们仅需几个关键要素:(1) 一个能压缩不断增长的历史数据的压缩器(如 RNN),反映当前对世界的认知;(2) 一个能持续改进该压缩器的学习算法(用以检测新模式);(3) 衡量压缩器因学习而产生的改进量(即可压缩性的一阶导数)的内在奖励;(4) 一个独立的强化学习器,它将内在奖励转化为能最大化未来学习进度的行动序列。这个有创造力的智能体被内在驱动,去不断地让新颖模式变得可预测、可压缩。
另一种总结: 除了外部奖励,一个主观观察者能从一系列行动和观察中获得多少乐趣?他的内在乐趣,等于他学习前后编码这些数据所需资源(比特与时间)的差值。一个独立的强化学习器,通过寻找或创造那些能以某种未知但可学习的方式被更好压缩的数据——例如笑话、歌曲、画作,或遵循全新物理定律的科学观测——来最大化预期的乐趣。